Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

VnDoc.com

Lý thuyết Toán 10 Bài tập cuối chương 5 CTST

Sách Chân trời sáng tạo

1 11

Bài trước

Bài sau

Lý thuyết Toán lớp 10 Bài tập cuối chương 5 được VnDoc sưu tầm và tổng hợp các câu hỏi lí thuyết và trắc nghiệm có đáp án đi kèm nằm trong chương trình giảng dạy môn Toán lớp 10 sách CTST. Mời quý thầy cô cùng các bạn tham khảo tài liệu dưới đây.

Bài tập cuối chương 5

A. Lý thuyết Toán 10 bài tập cuối chương 5
B. Trắc nghiệm Toán 10 bài tập cuối chương 5

A. Lý thuyết Toán 10 bài tập cuối chương 5

1. Khái niệm vectơ

a) Định nghĩa vectơ

Đại lượng vô hướng là đại lượng chỉ có độ lớn. Ví dụ: khối lượng, khoảng cách, nhiệt độ, ...

Đại lượng có hướng là đại lượng bao gồm cả đô lớn và hướng. Ví du: đo dịch chuyền, lực, vận tốc, gia tộc,

Khi xác định một đại lượng vô hướng, ta chỉ cần mô tả độ lớn của nó. Ví dụ: Hàng trên tàu có khối lượng 500 tân.

Khi xác định một đại lượng có hướng, ta phải đề cập đến cả độ lớn và hướng của nó. Ví dụ: Con tàu có độ địch chuyển đài 500 km theo hướng từ A đến B.

Vecto là một đoạn thẳng có hướng, nghĩa là đã chỉ ra điểm đầu và điểm cuối.

* Vectơ có điểm đầu A, điểm cuối B được kí hiệu là $\overrightarrow {AB}$ , đọc là vectơ $\overrightarrow {AB}$ (Hình sau)

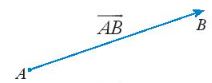
* Đường thẳng đi qua hai điểm A và B gọi là giá của vectơ $\overrightarrow {AB}$

* Độ dài của đoạn thẳng AB gọi là độ đài của vectơ V và được kí hiệu là $\left| {\overrightarrow {AB} {\rm{ }}} \right|$ Như vậy ta có: $\left| {\overrightarrow {AB} {\rm{ }}} \right| = AB$ .

Chú ý: Một vectơ khi không cần chỉ rõ điểm đầu và điểm cuối có thể viết là $\overrightarrow a ,\overrightarrow b ,\overrightarrow x ,\overrightarrow y$ ...

b) Hai vectơ cùng phương, cùng hướng

+) Hai vecto được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.

+) Hai vecto cùng phương thì chúng cùng hướng hoặc ngược hướng.

c) Vectơ bằng nhau - Vectơ đối nhau

+) Hai vecto được gọi là bằng nhau nếu chúng có cùng độ dài và cùng hướng.

+) Hai vecto được gọi là đối nhau nếu chúng có cùng độ dài và ngược hướng.

Kí hiệu: $\overrightarrow a = - \overrightarrow b , (vecto \overrightarrow b)$ là vecto đối của vecto $\overrightarrow a$

Chú ý: Với mỗi điểm O và vecto $\overrightarrow a$ cho trước, có duy nhất điểm A sao cho $\overrightarrow {OA} = \overrightarrow a$

d) Vectơ không

Vecto không, là vecto có điểm đầu và điểm cuối trùng nhau. Kí hiệu chung là $\overrightarrow 0 .$

* Chú ý:

- Vecto không có độ dài bằng 0.

- Vecto $\overrightarrow 0 .$ cùng phương, cùng hướng với mọi vecto.

- Mọi vecto-không đều bằng nhau: $\overrightarrow 0 = \overrightarrow {AA} = \;\overrightarrow {BB} = ...$

- Vecto đối của vecto-không là chính nó.

2. Tổng và hiệu của hai vectơ

a) Tổng của hai vectơ

Cho hai vectơ $\overrightarrow a$ và $\overrightarrow b$ . Từ một điểm A tùy ý, lấy hai điểm B, C sao cho $\overrightarrow {AB} = \overrightarrow a , \overrightarrow {BC} = \overrightarrow b$ . Khi đó $\overrightarrow {AC}$ được gọi là tổng của hai vecto $\overrightarrow a, \overrightarrow b$ được kí hiệu là $\overrightarrow a + \overrightarrow b$

Vậy $\overrightarrow a + \overrightarrow b = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC}$

Quy tắc ba điểm:

Với 3 điểm M, N, P ta có: $\overrightarrow {MN} + \overrightarrow {NP} = \overrightarrow {MP}$

Quy tắc hình bình hành:

Nếu OABC là hình bình hành thì ta có $\overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow {OB}$

Chú ý:

+ Khi cộng hai vectơ theo quy tắc ba điểm, điểm cuối của vectơ thứ nhất phải là điểm đầu của vectơ thứ hai.

b) Tính chất của phép cộng các vectơ

Phép cộng vecto có các tính chất sau:

+ Tính chất giao hoán: $\overrightarrow a + \overrightarrow b = \overrightarrow b + \overrightarrow a$

+ Tính chất kết hợp: $(\overrightarrow a + \overrightarrow b ) + \overrightarrow c = \overrightarrow a + (\overrightarrow b + \overrightarrow c )$

+ Với mọi vecto $\overrightarrow a ,$ ta luôn có: $\overrightarrow a + \overrightarrow 0 = \overrightarrow 0 + \overrightarrow a = \overrightarrow a$

Chú ý: $\overrightarrow a + ( - \overrightarrow a ) = \overrightarrow 0$ (Tổng hai vecto đối luôn bằng vecto-không)

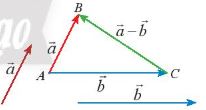
c) Hiệu của hai vectơ

Hiệu của hai vecto $\overrightarrow a - \overrightarrow b = \overrightarrow a + \left( { - \overrightarrow b } \right)$

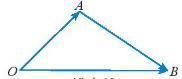
Chú ý: Cho ba điểm O, A, B ta có: $\overrightarrow {OB} - \overrightarrow {OA} = \overrightarrow {AB}$

d) Tính chất vectơ của trung điểm đoạn thẳng và trọng tâm tam giác

+) M là trung điểm AB $\Leftrightarrow \overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0$

+) G là trọng tâm của $\Delta ABC \Leftrightarrow \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0$

3. Tích của một số với một vectơ

a) Tích của một số với một vecto và các tính chất

+) Tích của một số thực k với một vecto $\overrightarrow a \ne \overrightarrow 0$ là một vecto, kí kiệu là $k\overrightarrow a .$

+) Vecto $k\overrightarrow a$ có độ dài bằng $\left| k \right|\left| {\overrightarrow a } \right|$ và c ùng hướng với vecto $\overrightarrow a$ nếu (k > 0), ngược hướng với vecto $\overrightarrow a$ nếu (k < 0)

+) Quy ước: $0\;\overrightarrow a = \overrightarrow 0$ và $k\;\overrightarrow 0 = \overrightarrow 0$

+) Tính chất: Với hai vecto $\overrightarrow a ,\overrightarrow b$ và hai số thực (k, t) ta luôn có:

$\begin{array}{l}k(t\overrightarrow a ) = (kt)\;\overrightarrow a \\(k + t)\,\overrightarrow a = k\overrightarrow a + t\overrightarrow a \\k(\overrightarrow a + \overrightarrow b ) = k\overrightarrow a + k\overrightarrow b ;\quad k(\overrightarrow a - \overrightarrow b ) = k\overrightarrow a - k\overrightarrow b \\1\;\overrightarrow a = \overrightarrow a ;\;\;( - 1)\;\overrightarrow a = - \,\overrightarrow a \end{array}$

b) Điều kiện để hai vecto cùng phương

Hai vecto $\overrightarrow a$ và $\overrightarrow b, \overrightarrow b$ khác $\overrightarrow 0$ )) cùng phương khi và chỉ khi tồn tại k sao cho $\overrightarrow a = k\overrightarrow b .$

Nhận xét: Ba điểm phân biệt A, B, C thẳng hàng $\Leftrightarrow \overrightarrow {AB} = k\overrightarrow {AC} .$

Chú ý: Cho hai vecto $\overrightarrow a$ và $\overrightarrow b$ không cùng phương. Với mỗi vecto $\overrightarrow c$ luôn tồn tại duy nhất cặp số thực (m; n) sao cho $\overrightarrow c = m\,\overrightarrow a + n\,\overrightarrow b$

4. Tích vô hướng của hai vectơ

a) Góc giữa hai vectơ

Cho hai vecto $\overrightarrow u$ và $\overrightarrow v$ khác $\overrightarrow 0$ . Góc giữa hai vecto $\overrightarrow u$ và $\overrightarrow v$ , kí hiệu $\left( {\;\overrightarrow u ,\overrightarrow v } \right)$

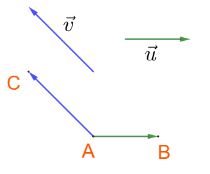
*Cách xác định góc

Chọn điểm A bất kì, vẽ $\overrightarrow {AB} = \overrightarrow u$ và $\overrightarrow {AC} = \overrightarrow v$ . Khi đó $\left( {\;\overrightarrow u ,\overrightarrow v } \right) = \widehat {BAC}$

* Các trường hợp đặc biệt:

+) $\left( {\;\overrightarrow u ,\overrightarrow 0 } \right) = \alpha$ tùy ý, với ${0^ \circ } \le \alpha \le {180^ \circ }$

+) $\left( {\;\overrightarrow u ,\overrightarrow v } \right) = {90^ \circ } \Leftrightarrow \overrightarrow u \bot \overrightarrow v$ hoặc $\overrightarrow v \bot \overrightarrow u$ . Đặc biệt: $\overrightarrow 0 \bot \overrightarrow u \;\;\forall \overrightarrow u \;$

+) $\left( {\;\overrightarrow u ,\overrightarrow v } \right) = {0^ \circ } \Leftrightarrow \overrightarrow u ,\overrightarrow v$ cùng hướng

+) $\left( {\;\overrightarrow u ,\overrightarrow v } \right) = {180^ \circ } \Leftrightarrow \overrightarrow u ,\overrightarrow v$ ngược hướng

Chú ý:

- Từ định nghĩa ta có $\left( {\overrightarrow a ,\overrightarrow b } \right) = \left( {\overrightarrow b ,\overrightarrow a } \right)$

- Góc giữa hai vectơ cùng hướng và khác ${\overrightarrow 0 }$ luôn bằng 00

- Góc giữa hai vectơ ngược hướng và khác ${\overrightarrow 0 }$ ) luôn bằng 1800,

- Trong trường hợp có ít nhất một trong hai vectơ ${\overrightarrow a }$ hoặc ${\overrightarrow b }$ là vectơ ${\overrightarrow 0 }$ thì ta quy ước

số đo góc giữa hai vectơ đó là tùy ý (từ 00 đến 1800)

b) Tích vô hướng của hai vectơ

Tích vô hướng của hai vecto $\overrightarrow u ,\;\overrightarrow v : \overrightarrow u .\;\overrightarrow v = \left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right|.\cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right)$

Chú ý:

+) $\overrightarrow u .\;\overrightarrow v \;\; = 0 \Leftrightarrow \overrightarrow u \bot \;\overrightarrow v \;\;$

+) $\overrightarrow u .\;\overrightarrow u \;\; = {\overrightarrow u ^2} = \left| {\overrightarrow u } \right|.\left| {\overrightarrow u } \right|.\cos {0^ \circ } = {\left| {\overrightarrow u } \right|^2}$