Lý thuyết Toán 10 bài 1: Giá trị lượng giác của một góc từ 0˚ đến 180˚ CTST

Sách Chân trời sáng tạo

VnDoc xin trân trọng giới thiệu bài Lý thuyết Toán lớp 10 bài 1: Giá trị lượng giác của một góc từ 0˚ đến 180˚ được chúng tôi sưu tầm và tổng hợp các câu hỏi lí thuyết và trắc nghiệm có đáp án đi kèm nằm trong chương trình giảng dạy môn Toán lớp 10 sách CTST. Mời quý thầy cô cùng các bạn tham khảo tài liệu dưới đây.

Giá trị lượng giác của một góc từ 0˚ đến 180˚

A. Lý thuyết Toán 10 bài 11
B. Bài tập minh họa
C. Trắc nghiệm Toán 10 bài 11

A. Lý thuyết Toán 10 bài 1

1. Giá trị lượng giác

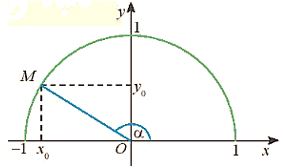
+) Với mỗi góc $\alpha ({0^o} \le \alpha \le {180^o})$ $\alpha ({0^o} \le \alpha \le {180^o})$có duy nhất điểm $M({x_0};{y_0})$ $M({x_0};{y_0})$ trên nửa đường tròn đơn vị để $\widehat {xOM} = \alpha .$ $\widehat {xOM} = \alpha .$ Khi đó:

$\sin \alpha = {y_0}$ $\sin \alpha = {y_0}$ là tung độ của M

$\cos \alpha = {x_0}$ $\cos \alpha = {x_0}$là hoành độ của M

$\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{{y_0}}}{{{x_0}}}(\alpha \ne {90^o})$ $\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{{y_0}}}{{{x_0}}}(\alpha \ne {90^o})$

$\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{{{x_0}}}{{{y_0}}}(\alpha \ne {0^o},\alpha \ne {180^o})$ $\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{{{x_0}}}{{{y_0}}}(\alpha \ne {0^o},\alpha \ne {180^o})$

Ví dụ: Tìm các giá trị lượng giác của góc 120°.

Giải

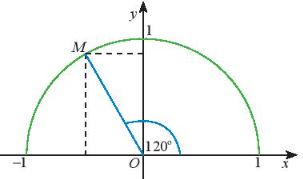
Lấy điểm M trên nửa đường tròn đơn vị sao cho.

$\widehat {xOM} = {120^0}$ $\widehat {xOM} = {120^0}$. Ta có $\widehat {MOy} = {120^0} - {90^0} = {30^0}.$ $\widehat {MOy} = {120^0} - {90^0} = {30^0}.$

Ta tính được tọa độ điểm M là $\left( { - \frac{1}{2};\frac{{\sqrt 3 }}{2}} \right)$ $\left( { - \frac{1}{2};\frac{{\sqrt 3 }}{2}} \right)$

Vậy theo định nghĩa ta có:

$\begin{array}{l} \sin {120^0} = \frac{{\sqrt 3 }}{2};cos{120^0} = - \frac{1}{2};\\ \tan {120^0} = - \sqrt 3 ;\cot {120^0} = - \frac{{\sqrt 3 }}{3}. \end{array}$ $\begin{array}{l} \sin {120^0} = \frac{{\sqrt 3 }}{2};cos{120^0} = - \frac{1}{2};\\ \tan {120^0} = - \sqrt 3 ;\cot {120^0} = - \frac{{\sqrt 3 }}{3}. \end{array}$

Chú ý:

a) Nếu α là góc nhọn thì các giá trị lượng giác của α đều dương

Nếu ơ là góc tù thì sin α> 0, cosα < 0, tanα < 0, cotα < 0.

b) tanα chỉ xác định khi $\alpha \ne {90^0}$ $\alpha \ne {90^0}$

cotα chỉ xác định khi $\alpha \ne {0^0}$ $\alpha \ne {0^0}$ và $\alpha \ne {180^0}.$ $\alpha \ne {180^0}.$

2. Quan hệ giữa các giá trị lượng giác của hai góc bù nhau

Hai góc bù nhau, $\alpha và {180^o} - \alpha$ $\alpha và {180^o} - \alpha$:

$\begin{array}{l}\sin \left( {{{180}^o} - \alpha } \right) = \sin \alpha \\\cos \left( {{{180}^o} - \alpha } \right) = - \cos \alpha \\\tan \left( {{{180}^o} - \alpha } \right) = - \tan \alpha (\alpha \ne {90^o})\\\cot \left( {{{180}^o} - \alpha } \right) = - \cot \alpha ({0^o} < \alpha < {180^o})\end{array}$ $\begin{array}{l}\sin \left( {{{180}^o} - \alpha } \right) = \sin \alpha \\\cos \left( {{{180}^o} - \alpha } \right) = - \cos \alpha \\\tan \left( {{{180}^o} - \alpha } \right) = - \tan \alpha (\alpha \ne {90^o})\\\cot \left( {{{180}^o} - \alpha } \right) = - \cot \alpha ({0^o} < \alpha < {180^o})\end{array}$

Hai góc phụ nhau, α và ${90^o} - \alpha$ ${90^o} - \alpha$:

$\begin{array}{l}\sin \left( {{{90}^o} - \alpha } \right) = \cos \alpha \\\cos \left( {{{90}^o} - \alpha } \right) = \sin \alpha \\\tan \left( {{{90}^o} - \alpha } \right) = \cot \alpha (\alpha \ne {90^o},{0^o} < \alpha < {180^o})\\\cot \left( {{{90}^o} - \alpha } \right) = \tan \alpha (\alpha \ne {90^o},{0^o} < \alpha < {180^o})\end{array}$ $\begin{array}{l}\sin \left( {{{90}^o} - \alpha } \right) = \cos \alpha \\\cos \left( {{{90}^o} - \alpha } \right) = \sin \alpha \\\tan \left( {{{90}^o} - \alpha } \right) = \cot \alpha (\alpha \ne {90^o},{0^o} < \alpha < {180^o})\\\cot \left( {{{90}^o} - \alpha } \right) = \tan \alpha (\alpha \ne {90^o},{0^o} < \alpha < {180^o})\end{array}$

Ví dụ: Cho biết $\sin {30^0} = \frac{1}{2};cos{45^0} = \frac{{\sqrt 2 }}{2};\tan {60^0} = \sqrt 3$ $\sin {30^0} = \frac{1}{2};cos{45^0} = \frac{{\sqrt 2 }}{2};\tan {60^0} = \sqrt 3$. Tính $\sin {150^0};cos{135^0};\tan {120^0}.$ $\sin {150^0};cos{135^0};\tan {120^0}.$

Giải

$\begin{array}{l} \sin {150^0} = \sin \left( {{{180}^0} - {{30}^0}} \right) = \sin {30^0} = \frac{1}{2};\\ cos{135^0} = - cos{45^0} = - \frac{{\sqrt 2 }}{2};\\ \tan {120^0} = - \tan {60^0} = - \sqrt 3 . \end{array}$ $\begin{array}{l} \sin {150^0} = \sin \left( {{{180}^0} - {{30}^0}} \right) = \sin {30^0} = \frac{1}{2};\\ cos{135^0} = - cos{45^0} = - \frac{{\sqrt 2 }}{2};\\ \tan {120^0} = - \tan {60^0} = - \sqrt 3 . \end{array}$

3. Giá trị lượng giác của một số góc đặc biệt

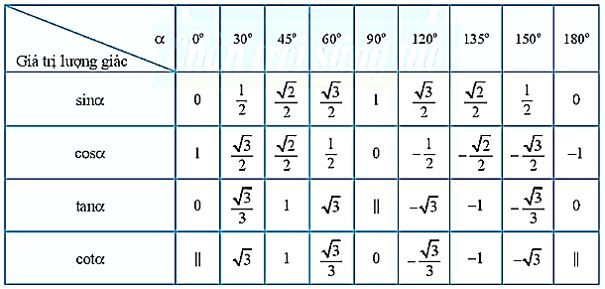
Chú ý: Trong bảng, kí hiệu "||" để chỉ giá trị lượng giác không xác định.

1.4. Sử dụng máy tính cầm tay để tính giá trị lượng giác của một góc

a) Tính các giá trị lượng giác của góc

Bước 1: Cài đặt đơn vị đo góc (độ hoặc radian)

Bước 2: Vào chế độ tính toán

Chú ý: Để tính $\cot \alpha$ $\cot \alpha$ta tính $\frac{1}{{\tan \alpha }}$ $\frac{1}{{\tan \alpha }}$.

b) Xác định số đo của góc khi biết giá trị lượng giác của góc đó

Để tìm $\alpha$ $\alpha$khi biết $\cot \alpha$ $\cot \alpha$ ta tính $\tan \alpha = \frac{1}{{\cot \alpha }}$ $\tan \alpha = \frac{1}{{\cot \alpha }}$ rồi tính $\alpha$ $\alpha$ sau.

B. Bài tập minh họa

Câu 1: Tính các giá trị lượng giác: $\sin {120^o};\cos {150^o};\cot {135^o}.$ $\sin {120^o};\cos {150^o};\cot {135^o}.$

Hướng dẫn giải

$\begin{array}{l}\sin {120^o} = \sin \;({180^o} - {60^o}) = \sin {60^o} = \frac{{\sqrt 3 }}{2};\\\cos {150^o} = - \cos \;({180^o} - {30^o}) = - \cos {30^o} = - \frac{{\sqrt 3 }}{2};\\\cot {135^o} = - \cot \;({180^o} - {45^o}) = - \cot {45^o} = - 1.\end{array}$ $\begin{array}{l}\sin {120^o} = \sin \;({180^o} - {60^o}) = \sin {60^o} = \frac{{\sqrt 3 }}{2};\\\cos {150^o} = - \cos \;({180^o} - {30^o}) = - \cos {30^o} = - \frac{{\sqrt 3 }}{2};\\\cot {135^o} = - \cot \;({180^o} - {45^o}) = - \cot {45^o} = - 1.\end{array}$

Câu 2: Cho biết $\sin \alpha = \frac{1}{2},$ $\sin \alpha = \frac{1}{2},$ tìm góc $\alpha \;({0^o} \le \alpha \le {180^o})$ $\alpha \;({0^o} \le \alpha \le {180^o})$ bằng cách vẽ nửa đường tròn đơn vị.

Hướng dẫn giải

Gọi M là điểm thuộc nửa đường tròn đơn vị sao cho: $\widehat {xOM} = \alpha$ $\widehat {xOM} = \alpha$

Do $\sin \alpha = \frac{1}{2}$ $\sin \alpha = \frac{1}{2}$ nên tung độ của M bằng $\frac{1}{2}.$ $\frac{1}{2}.$

Vậy ta xác định được hai điểm N và M thỏa mãn $\sin \widehat {xON} = \sin \widehat {xOM} = \frac{1}{2}$ $\sin \widehat {xON} = \sin \widehat {xOM} = \frac{1}{2}$

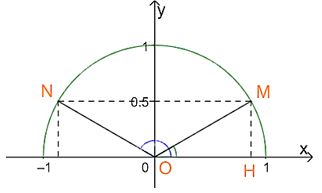
Đặt \ $\beta = \widehat {xOM} \Rightarrow \widehat {xON} = {180^o} - \beta$ $\beta = \widehat {xOM} \Rightarrow \widehat {xON} = {180^o} - \beta$

Xét tam giác OHM vuông tại H ta có: $MH = \frac{1}{2} = \frac{{OM}}{2} \Rightarrow \beta = {30^o}$ $MH = \frac{1}{2} = \frac{{OM}}{2} \Rightarrow \beta = {30^o}$

$\Rightarrow \widehat {xON} = {180^o} - {30^o} = {150^o}$ $\Rightarrow \widehat {xON} = {180^o} - {30^o} = {150^o}$

Vậy $\alpha = {30^o} hoặc \alpha = {150^o}$ $\alpha = {30^o} hoặc \alpha = {150^o}$

Câu 3: Tính:

$A = \sin {150^o} + \tan {135^o} + \cot {45^o}$ $A = \sin {150^o} + \tan {135^o} + \cot {45^o}$

$B = 2\cos {30^o} - 3\tan 150 + \cot {135^o}$ $B = 2\cos {30^o} - 3\tan 150 + \cot {135^o}$

Hướng dẫn giải

$A = \sin {150^o} + \tan {135^o} + \cot {45^o}$ $A = \sin {150^o} + \tan {135^o} + \cot {45^o}$

Sử dụng bảng giá trị lượng giác của một số góc đặc biệt, ta có:

$\sin {150^o} = \frac{1}{2};\tan {135^o} = - 1;\cot {45^o} = 1.$ $\sin {150^o} = \frac{1}{2};\tan {135^o} = - 1;\cot {45^o} = 1.$

$\Rightarrow A = \frac{1}{2} - 1 + 1 = \frac{1}{2}.$ $\Rightarrow A = \frac{1}{2} - 1 + 1 = \frac{1}{2}.$

$B = 2\cos {30^o} - 3\tan 150 + \cot {135^o}$ $B = 2\cos {30^o} - 3\tan 150 + \cot {135^o}$

Sử dụng bảng giá trị lượng giác của một số góc đặc biệt, ta có:

$\cos {30^o} = \frac{{\sqrt 3 }}{2};\tan {150^o} = - \frac{{\sqrt 3 }}{3};\cot {135^o} = - 1.$ $\cos {30^o} = \frac{{\sqrt 3 }}{2};\tan {150^o} = - \frac{{\sqrt 3 }}{3};\cot {135^o} = - 1.$

$\Rightarrow B = 2.\frac{{\sqrt 3 }}{2} - 3.\left( { - \frac{{\sqrt 3 }}{3}} \right) + 1 = 5\sqrt 3 + 1.$ $\Rightarrow B = 2.\frac{{\sqrt 3 }}{2} - 3.\left( { - \frac{{\sqrt 3 }}{3}} \right) + 1 = 5\sqrt 3 + 1.$