Lý thuyết Toán 10 bài 3: Các phép toán trên tập hợp CTST
VnDoc xin trân trọng giới thiệu bài Lý thuyết Toán lớp 10 bài 3: Các phép toán trên tập hợp được chúng tôi sưu tầm và tổng hợp các câu hỏi lí thuyết và trắc nghiệm có đáp án đi kèm nằm trong chương trình giảng dạy môn Toán lớp 10 sách CTST. Mời quý thầy cô cùng các bạn tham khảo tài liệu dưới đây.
Bài: Các phép toán trên tập hợp
A. Lý thuyết Toán 10 bài 3
1. Hợp và giao của các tập hợp
– Cho hai tập hợp A và B.
Tập hợp các phần tử thuộc A hoặc thuộc B gọi là hợp của hai tập hợp A và B, kí hiệu A ∪ B.
A ∪ B = {x| x ∈ A hoặc x ∈ B}.
Tập hợp các phần tử thuộc cả hai tập hợp A và B gọi là giao của hai tập hợp A và B, kí hiệu A ∩ B.
A ∩ B = {x | x ∈ A và x ∈ B}.
Nhận xét:
+ Nếu A và B là hai tập hợp hữu hạn thì n(A ∪ B) = n(A) + n(B) – n(A ∩ B).
+ Đặc biệt, nếu A và B không có phần tử chung, tức A ∩ B = ∅, thì n(A ∪ B) = n(A) + n(B).
Ví dụ 1.
a) Cho hai tập hợp S = {1; 2; 3; 4} và T = {5; 6; 7}. Hãy xác định N = S ∪ T.
b) Cho hai tập hợp A = {x ∈ ℝ| (2x – x2)(2x2 – 3x – 2) = 0} và B = {n ∈ ℕ| 3 < n2 < 30}. Hãy xác định A ∩ B.
Hướng dẫn giải
a) Hợp của hai tập hợp S và T là tập hợp N = S ∪ T = {1; 2; 3; 4; 5; 6; 7}.
b) Xét tập hợp A = {x ∈ ℝ| (2x – x2)(2x2 – 3x – 2) = 0} ta có (2x – x2)(2x2 – 3x – 2) = 0
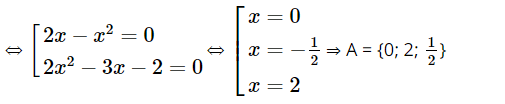
Xét tập hợp B = {n ∈ ℕ| 3 < n2 < 30} = {2; 3; 4; 5}.
Do đó A ∩ B = {2}.
2. Hiệu của hai tập hợp, phần bù của tập con
– Cho hai tập hợp A và B.
Tập hợp các phần tử thuộc A nhưng không thuộc B gọi là hiệu của A và B, kí hiệu A\B.
A\B = {x | x ∈ A và x ∉ B}.
Nếu A là tập con của E thì hiệu E\A gọi là phần bù của A trong E, kí hiệu CEA.
Chú ý: Trong các chương sau, để tìm các tập hợp là hợp, giao, hiệu, phần bù của những tập con của tập số thực, ta thường vẽ sơ đồ trên trục số.
Ví dụ 2. Cho hai tập hợp S = {2; 3; 4; 5; 6; 7; 8; 9} và T = {4; 5; 6; 7}.
Hãy xác định S\T và CST.
Hướng dẫn giải
Hiệu của S và T là S\T = {2; 3; 8; 9}.
Ta thấy T là tập con của S nên phần bù của T trong S chính là:
CST = S\T = {2; 3; 8; 9}.
Ví dụ 3. Xác định tập hợp:
a) A = [–3; 3] ∩ (1; +∞);
b) B = (7; 12] ∪ (‒∞; 9].
Hướng dẫn giải
a) Để xác định tập hợp A, ta vẽ sơ đồ sau đây:

Từ sơ đồ, ta thấy A = (1; 3].
b) Để xác định tập hợp B, ta vẽ sơ đồ sau đây:

Từ sơ đồ, ta thấy B = (‒∞; 12].
B. Bài tập Toán 10 bài 3
1. Bài tập trắc nghiệm
Câu 1. Cho A = {(x; y)| x, y ∈ ℝ, 3x – y = 7}, B = {(x; y)| x, y ∈ ℝ, x – y = 1}.
Tập hợp A ∩ B là:
A. {(3; 2)};
B. {3}, {2};
C. {3; 2};
D. ∅.
Hướng dẫn giải
Đáp án đúng là: A
Tập hợp A ∩ B là tập hợp cặp số (x; y) thỏa mãn hệ phương trình:
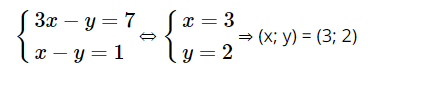
Vậy A ∩ B = {(3; 2)}.
Ta chọn phương án A.
Câu 2. Trong các tập hợp sau đây, tập hợp nào bằng tập hợp M = ℝ\(–∞; 2):
A. A = (‒∞; –2);
B. B = (‒∞; 2);
C. C = (2; +∞);
D. D = [2; +∞).
Hướng dẫn giải
Đáp án đúng là: D
Ta có tập hợp M = ℝ\(–∞; 2) = [2; +∞).
Vậy phương án D đúng.
Câu 3. Cho các tập hợp A, B, C được minh hoạ bằng biểu đồ Ven như hình vẽ dưới đây:

Phần tô màu xám trong hình vẽ biểu diễn của tập hợp nào sau đây?
A. A ∩ B ∩ C;
B. (A\B) ∪ (A\C);
C. (A ∪ B) \ C;
D. (A ∩ B) \ C.
Hướng dẫn giải
Đáp án đúng là: D
Phần tô màu xám trong hình là biểu diễn tập hợp các điểm vừa thuộc A, thuộc B mà không thuộc C.
Đó chính là tập (A ∩ B) \ C.
Ta chọn phương án D.
2. Bài tập tự luận
Bài 1. Xác định tập hợp A ∩ B và A ∪ B trong mỗi trường hợp sau:
a) A = {x ∈ ℕ | x ⋮ 4, x < 30}, B = {x ∈ ℕ | x ⋮ 5, x < 30}.
b) C = {x ∈ ℝ| 2x + 4 > 0, x < 5} và D = {x ∈ ℝ| (x + 3)(x – 4) ≤ 0}.
Hướng dẫn giải
a) Ta xác định các phần tử của tập hợp A và tập hợp B.
A = {0; 4; 8; 12; 16; 20; 24; 28}.
B = {0; 5; 10; 15; 20; 25}.
Suy ra A ∩ B = {0; 20};
A ∪ B = {0; 4; 5; 8; 10; 12; 15; 16; 20; 24; 25; 28}.
b) Ta xác định các phần tử của tập hợp C và tập hợp D.
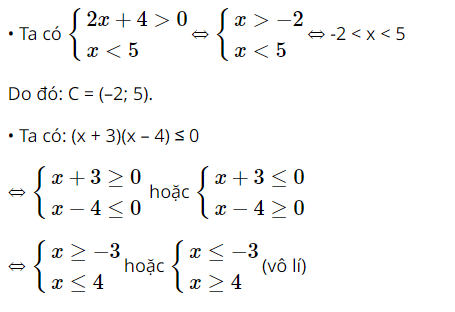
⇔ –3 ≤ x ≤ 4.
Do đó: D = [–3; 4].
Ta có sơ đồ sau:

Từ sơ đồ, ta thấy C ∩ D = (–2; 4] và C ∪ D = [–3; 5).
Bài 2. Lớp 10A của trường có 33 học sinh, trong đó có 20 học sinh thích môn Toán, 18 học sinh thích môn Ngữ Văn và 10 học sinh thích cả môn Toán và Ngữ Văn. Hỏi lớp 10A có:
a) Bao nhiêu học sinh thích ít nhất 1 trong 2 môn Toán và môn Ngữ Văn?
b) Bao nhiêu học sinh không thích môn nào?
Hướng dẫn giải
a) Gọi A là tập hợp số học sinh thích môn Toán.
B là tập hợp số học sinh thích môn Ngữ Văn.
Số phần tử của A và B lần lượt là n(A) và n(B) thì n(A) = 20, n(B) = 18.
Ta có:
+) Tập hợp số học sinh thích cả môn Toán và Ngữ Văn là A ∩ B nên n(A ∩ B) = 10.
+) Tập hợp số học sinh thích ít nhất 1 trong 2 môn Toán và môn Ngữ Văn là A ∪ B.
Nên tổng số học sinh thích ít nhất 1 trong 2 môn Toán và môn Ngữ Văn là n(A ∪ B).
Suy ra n(A ∪ B) = n(A) + n(B) ‒ n(A ∩ B) = 20 + 18 – 10 = 28.
Vậy có 28 học sinh thích ít nhất 1 trong 2 môn Toán và môn Ngữ Văn.
b) Số học sinh không thích môn học nào là: 33 – 28 = 5 (học sinh)
Vậy có 5 học sinh không thích môn học nào trong hai môn Toán và môn Ngữ Văn.
Bài 3. Cho U = {x ∈ ℕ | x < 20}, A = {x ∈ U | x là bội của 4}, B = {x ∈ U | x là ước của 12}. Xác định các tập hợp A\B, B\A, CUA, CUB, CU(A ∪ B), CU( A ∩ B).
Hướng dẫn giải
Ta xác định các phần tử của tập hợp U, A, B.
U = {x ∈ ℕ | x < 20} = {0; 1; 2; 3; 4; …; 19}.
A = {x ∈ U | x là bội của 4} = {0; 4; 8; 12; 16}.
B = {x ∈ U | x là ước của 12} = {1; 2; 3; 4; 6; 12}.
Khi đó ta có:
A\B = {0; 8; 16}.
B\A = {1; 2; 3; 6}.
CUA = {1; 2; 3; 5; 6; 7; 9; 10; 11; 13; 14; 15; 17; 18; 19}.
CUB = {0; 5; 7; 8; 9; 10; 11; 13; 14; 15; 16; 17; 18; 19}.
A ∩ B = {4; 12}, A ∪ B = {0; 1; 2; 3; 4; 6; 8; 12; 16}.
CU(A ∪ B) = {5; 7; 9; 10; 11; 13; 14; 15; 17; 18; 19}.
CU(A ∩ B) = {1; 2; 3; 5; 6; 7; 8; 9; 10; 11; 13; 14; 15; 16; 17; 18; 19}.
C. Trắc nghiệm Toán 10 bài 3
-----------------------------------------
Như vậy VnDoc đã giới thiệu các bạn tài liệu Lý thuyết Toán lớp 10 bài 3: Các phép toán trên tập hợp. Mời các bạn tham khảo thêm tài liệu: Giải bài tập Toán lớp 10, Chuyên đề Toán 10, Giải Vở BT Toán 10 , Toán 10 Cánh Diều, Toán 10 Kết nối tri thức, Tài liệu học tập lớp 10.









