Lý thuyết Toán 10 Bài tập cuối chương 7 CTST

Sách Chân trời sáng tạo

VnDoc xin giới thiệu bài Lý thuyết Toán lớp 10 Bài tập cuối chương 7 được chúng tôi sưu tầm và tổng hợp các câu hỏi lí thuyết và trắc nghiệm có đáp án đi kèm nằm trong chương trình giảng dạy môn Toán lớp 10 sách CTST. Mời quý thầy cô cùng các bạn tham khảo tài liệu dưới đây.

Bài tập cuối chương 7

A. Lý thuyết Toán 10 bài tập cuối chương 7
B. Bài tập minh họa
C. Trắc nghiệm Toán 10 bài tập cuối chương 7

A. Lý thuyết Toán 10 bài tập cuối chương 7

1. Dấu của tam thức bậc hai

a) Tam thức bậc hai

Đa thức bậc hai f(x) = ax² + bx + c với a, b, c là hệ số, a ≠ 0 và x là biến số được gọi là tam thức bậc hai.

* Cho tam thức bậc hai f(x) = ax² + bx + c, a ≠ 0. Khi thay x bằng giá trị x0 vào ƒ(x), ta được $f\left( {{x_0}} \right) = a{x_0}^2 + b{x_0} + c$ , gọi là giá trị của tam thức bậc lai tại x0.

+ Nếu $f\left( {{x_0}} \right) > 0$ thì ta nói f(x) đương tại x0;

+ Nếu $f\left( {{x_0}} \right) < 0$ thì ta nói f(x) âm tại x0;

+ Nếu f(x) đương (âm) tại mọi điểm x thuộc một khoảng hoặc một đoạn thì ta nói f{x) dương (âm) trên khoảng hoặc đoạn đó.

* Cho tam thức bậc hai f(x) = ax² + bx + c, a ≠ 0. Khi đó

+ Nghiệm của phương trình bậc hai ax² + bx + c là nghiệm của f(x).

+ Biểu thức $\Delta = {b^2} - 4{\rm{a}}c; \Delta ' = {\left( {\frac{b}{2}} \right)^2} - ac$ lần lượt là biệt thức và biệt thức thu gọn của f(x).

b) Định lí về dấu của tam thức bậc hai

Cho tam thức bậc hai $f(x) = a{x^2} + bx + c\left( {a \ne 0} \right)$ .

+ Nếu Δ < 0 thì ƒ(x) cùng dấu với a với mọi giá trị x

+ Nếu Δ = 0 và \({x_0} = - $\frac{b}{{2{\rm{a}}}}$ là nghiệm kép của ƒ(x) thì ƒ(x) cùng dấu với a với mọi x khác x₀ .

+ Nến Δ > 0 và x₁, x₂ là hai nghiệm của $f(x)\left( {{x_1} < {x_2}} \right)$ thì ƒ(x) trái dấu với a với mọi x trong.

khoảng (x₁; x₂); f(x) cùng dấu với a với mọi x thuộc hai khoảng $\left( { - \infty ;{x_1}} \right),\left( {{x_2}; + \infty } \right)$

Chú ý

a) Để xét dâu tam thức bậc hai $f(x) = a{x^2} + bx + c\left( {a \ne 0} \right)$ , ta thực hiện các bước sau:

Bước 1: Tỉnh và xác định dấu của biệt thức Δ;

Bước 2: Xác định nghiệm của ƒ(x) (nếu có);

Bước 3: Xác định dấu của hệ số a,

Bước 4: Xác định dấu của ƒ(x)

b) Khi xét dấu của tam thức bậc hai, ta có thể dùng biệt thức thu gọn Δ' thay cho biệt thức Δ.

2. Giải bất phương trình bậc hai một ẩn

- Bất phương trình bậc hai một ẩn x là bất phương trình có một trong các dạng $a{x^2} + b{\rm{x}} + c \le 0,a{x^2} + b{\rm{x}} + c < 0,a{x^2} + b{\rm{x}} + c \ge 0,a{x^2} + b{\rm{x}} + c > 0; a \ne 0$

- Nghiệm của bất phương trình bậc hai là các giá trị của biến x mà khi thay vào bất phương trình ta được bắt đẳng thức đúng.

- Giải bất phương trình bậc hai là tìm tập hợp các nghiệm của bất phương trình đó.

- Ta có thể giải bất phương trình bậc hai bằng cách xét dấu của tam thức bậc hai tương ứng.

3. Phương trình quy về bậc hai

a) Phương trình dạng $\sqrt{ax^{2}+bx+c}=\sqrt{dx^{2}+ex+f}$

Để giải phương trình $\sqrt{ax^{2}+bx+c}=\sqrt{dx^{2}+ex+f}$ ta làm như sau:

Bước 1: Bình phương hai vế của phương trình để được phương trình $a{x^2} + bx + c = d{x^2} + ex + f$

Bước 2: Giải phương trình nhận được ở Bước 1

Bước 3: Thử lại xem các giá trị x tìm được ở Bước 2 có thỏa mãn phương trình đã cho hay không và kết luận nghiệm

b) Phương trình dạng $\sqrt{ax^{2}+bx+c}= dx+e$

Để giải phương trình $\sqrt{ax^{2}+bx+c}= dx+e$ , ta làm như sau:

Bước 1: Bình phương hai vế của phương trình để được phương trình $a{x^2} + bx + c = {\left( {dx + e} \right)^2}$

Bước 2: Giải phương trình nhận được ở Bước 1

Bước 3: Thử lại xem các giá trị x tìm được ở Bước 2 có thỏa mãn phương trình đã cho hay không và kết luận nghiệm.

B. Bài tập minh họa

Câu 1: Xét dấu của các tam thức bậc hai sau:

a) $f\left( x \right) = 2{x^2} - 3x - 2$

b) $g\left( x \right) = - {x^2} + 2x - 3$

Hướng dẫn giải

a) f(x) = 2x²- 3x - 2 có Δ = 25 > 0, hai nghiệm phân biệt là ${x_1} = - \frac{1}{2};{x_2} = 2$

và a = 2 > 0

Ta có bảng xét dấu như sau:

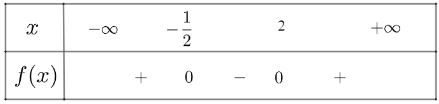
Vậy f(x) âm trong khoảng $\left( { - \frac{1}{2},2} \right)$ và dương trong hai khoảng

$\left( { - \infty , - \frac{1}{2}} \right); \left( {2, + \infty } \right)$

b) g(x) = - x² + 2x - 3 có Δ = 2² - 4. $\left( { - 1} \right).\left( { - 3} \right) = - 8 < 0$ và a = - 1 < 0

Vậy g(x) âm với mọi x ∈ R

Câu 3: Giải phương trình $\sqrt {31{x^2} - 58x + 1} = \sqrt {10{x^2} - 11x - 19}$

Hướng dẫn giải

Bình phương hai vế của phương trình đã cho, ta được:

$\begin{array}{l}\sqrt {31{x^2} - 58x + 1} = \sqrt {10{x^2} - 11x - 19} \\ \Rightarrow 31{x^2} - 58x + 1 = 10{x^2} - 11x - 19\\ \Rightarrow 21{x^2} - 47x + 20 = 0\end{array}\\$