VnDoc.com

Đề kiểm tra năng lực giáo viên môn Toán trường THPT Gia Bình, Bắc Ninh

Đóng

Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm

Mua VnDoc PRO chỉ từ 79.000đ

Đóng

Bạn cần đăng nhập tài khoản Thành viên VnDoc để:

- Xem đáp án

- Nhận 1 lần làm bài trắc nghiệm miễn phí!

Đăng nhập

Mô tả thêm:

Đề kiểm tra năng lực giáo viên môn Toán trường THPT Gia Bình, Bắc Ninh được VnDoc.com tổng hợp và xin gửi tới bạn đọc cùng tham khảo. Bài viết tổng hợp gồm có 50 câu hỏi trắc nghiệm có đáp án kèm theo. Mời các bạn cùng làm bài test dưới dây nhé.

Số câu hỏi: 50 câu
Số điểm tối đa: 50 điểm
Tài khoản: Đăng nhập

Trước khi làm bài bạn hãy

1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
4 Căn chỉnh thời gian làm từng câu một cách hợp lý

Câu 1: Nhận biết
Câu 1: Từ các chữ số 1,2,3,4,5,6,7 lập được bao nhiêu số tự nhiên gồm ba chữ số đôi một khác nhau?
- A.
  $C_{7}^{3}$
- B.
  $A_{7}^{3}$
- C.
  $P_{3}$
- D.
  $3^{7}$
Câu 2: Nhận biết
Câu 2:
- A.
  P = -13.
- B.
  B . P = -11.
- C.
  C . P = 5.
- D.
  D . P = -12.
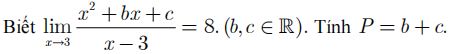
Câu 3: Nhận biết
Câu 3:
- A.
  A . M (2; 1;0)
- B.
  B . M (8;9;10)
- C.
  C . M (5;5;5)
- D.
  D . M (3; 4;5)
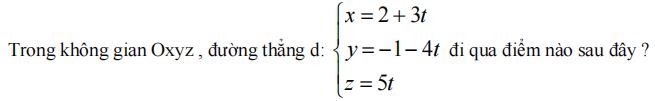
Câu 4: Nhận biết
Câu 4:
- A. cos²x = $\frac{3}{4}$
- B.
  cos²x = $\frac{\sqrt{3} }{2}$
- C.
  cos²x = $\frac{1}{4}$
- D.
  cos²x = $\frac{1}{2}$
Câu 5: Nhận biết
Câu 5:
- A.
  $m\;\in\;\left[2;6\right]$
- B.
  $m\;\in\;\left[-3;9\right]$
- C.
  $m\;\in\;\left(-\infty;2\right)\;\cup\;\left(5;+\infty\right)$
- D.
  $m\;\in\;\left(-9;3\right)$
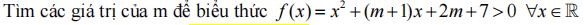
Câu 6: Nhận biết
Câu 6:

Cho hàm số y = ax⁴ + bx² + c (a, b, c $\in \mathbb{R}$ ) có đồ thị như hình vẽ bên.

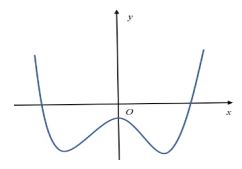
Số điểm cực trị của hàm số đã cho là
- A.
  2
- B.
  3
- C.
  1
- D.
  0
Câu 7: Nhận biết
Câu 7:

Cho sinx = $\frac{1}{2}$ và cosx nhận giá trị âm, giá trị của biểu thức $A = \frac{sinx - cosx}{sinx + cosx}$ bằng
- A.
  $-2-\sqrt{3}$
- B.
  2 + $\sqrt{3}$
- C.
  -2 + $\sqrt{3}$
- D.
  2 - $\sqrt{3}$
Câu 8: Nhận biết
Câu 8:

Cho khối nón tròn xoay có chiều cao và bán kính đáy cùng bằng a. Khi đó thể tích khối nón là
- A.
  A . $\frac{4}{3} \pi a^{3}$
- B.
  $\frac{2}{3} \pi a^{3}$
- C.
  $\pi a^{3}$
- D.
  $\frac{1}{3} \pi a^{3}$
Câu 9: Nhận biết
Câu 9:

Cho hàm số y = f(x) có bảng biến thiên như sau. Khẳng định nào dưới đây là sai?
- A.
  Phương trình f(x) = 0 vô nghiệm
- B.
  Hàm số có hai cực đại
- C.
  Đồ thị hàm số không có tiệm cận
- D.
  D . Hàm số nghịch biến trên khoảng $(1;+\infty )$
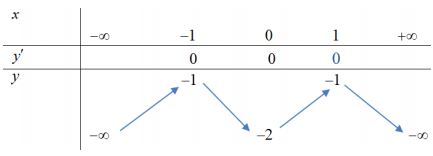
Câu 10: Nhận biết
Câu 10:

Trong mặt phẳng tọa độ Oxy nếu phép tịnh tiến biến điểm M (4;2) thành điểm M' (4;5) thì nó biến điểm A (2;5) thành điểm nào sau đây?
- A.
  A' (5;2)
- B.
  A' (2;5)
- C.
  A' (1;6)
- D.
  A' (2;8)
Câu 11: Nhận biết
Câu 11:

Cho hình chóp S.ABC có SA $\perp$ (ABC) và $\triangle$ ABC vuông ở B, AH là đường cao của $\triangle$ SAB . Khẳng định nào sau đây sai?
- A.
  AH $\perp$ AC
- B.
  AH $\perp$ BC
- C.
  SA $\perp$ BC
- D.
  AH $\perp$ SC
Câu 12: Nhận biết
Câu 12:

Trong không gian Oxyz, cho ba điểm A (1, 2. -3), B (2, 5, 7), C (-3, 1, 4). Tọa độ điểm D để tứ giác ABCD là hình bình hành là
- A.
  D (6;6;0)
- B.
  D (0, $\frac{8}{8} , \frac{8}{3}$ )
- C.
  D (0;8;8)
- D.
  D (4; 2; 6)
Câu 13: Nhận biết
Câu 13:

Trong mặt phẳng Oxy, cho đường tròn (C): (x - 2)² + (y+3)² = 9. Đường tròn có tâm và bán kính là
- A.
  I (2;3), R = 9
- B.
  I (2;-3), R = 3
- C.
  I (-3;2), R = 3
- D.
  I (-2;3), R = 3
Câu 14: Nhận biết
Câu 14:

Có bao nhiêu điểm trên đồ thị hàm số $y = -\frac{1}{3} x^{2} + 3x^{2} - 5x + \frac{7}{3}$ mà tiếp tuyến của đồ thị hàm số đã cho tại điểm đó song song với trục tung
- A.
  vô số
- B. 2
- C. 0
- D. 1
Câu 15: Nhận biết
Câu 15:

Với $\alpha$ là số thực dương tuỳ ý, ln(2018 $\alpha$ ) - ln(3 $\alpha$ ) bằng
- A.
  $ln\frac{2018}{3}$
- B.
  ln(2015 $\alpha$ )
- C.
  $\frac{ln(2018 )}{ln(3 )}$
- D.
  $\frac{ln 2018}{ln 3}$
Câu 16: Nhận biết
Câu 16:

Tìm giá trị thực của tham số m để hệ phương trình $\left\{\begin{array}{l}2x\;+\;3y\;+\;4\;=\;0\\3x\;+\;y\;-\;1\;=\;0\\2mx\;+\;5y\;-\;m\;=\;0\end{array}\right.$ có duy nhất một nghiệm
- A.
  m = 10.
- B. m = -10
- C.
  m = $-\frac{10}{3}$
- D.
  m = $\frac{10}{3}$
Câu 17: Nhận biết
Câu 17:

Phương trình 2x² + 3x - 1 = 0 có tổng hai nghiệm bằng
- A.
  Không tồn tại
- B.
  $-\frac{1}{2}$
- C.
  $\frac{3}{4}$
- D.
  $\frac{3}{2}$
Câu 18: Nhận biết
Câu 18:

Phương trình nào sau đây tương đương với phương trình x³ - 3x = 0?
- A.
  $x^{2} \sqrt{x - 3} = 3x \sqrt{x - 3}$
- B.
  $x^{2} + \frac{1}{x - 3} = 3x + \frac{1}{x - 3}$
- C.
  $x^{2} \sqrt{x^{2} + 1} = 3x \sqrt{x^{2} + 1}$
- D.
  $x^{2} \sqrt{x - 2} = 3x \sqrt{x - 2}$
Câu 19: Nhận biết
Câu 19:

Cho hàm số $f(x)\;=\;\left\{\begin{array}{l}\frac2{x\;-\;1}\;khi\;x\;\in(-\infty;0)\\\sqrt{x\;+\;1}\;khi\;x\;\in\;\left[0;2\right]\\x^2\;-\;1\;khi\;x\;\in\;(2;5)\;\end{array}\right.$ . Tính f(4)
- A.
  A . Không tính được.
- B.
  f(4) = $\frac{2}{3}$
- C.
  C . f(4) = 15.
- D.
  f(4) = $\sqrt{5}$
Câu 20: Nhận biết
Câu 20: Cho a > b khẳng định nào sau đây là đúng?
- A.
  A . 2a < 2b
- B.
  a > b - c, $\forall c\in \mathbb{R}$
- C.
  -a < -b
- D.
  ac > ab, $\forall c\in \mathbb{R}$
Câu 21: Nhận biết
Câu 21:

Cho hàm số f(x) liên tục trên $\mathbb{R}$ và có $\int_0^1f(x)dx\;=\;2;\;\int_0^3f(x)dx\;=\;6.$ Tính $I\;=\;\int_{-1}^1\;f(\left|2x\;-\;1\right|)dx$
- A.
  A . I = 8
- B.
  I = 16
- C.
  I = $\frac{3}{2}$
- D.
  I = 4
Câu 22: Nhận biết
Câu 22:

Trong không gian với hệ trục toạ độ Oxyz, cho tứ diện ABCD có điểm A (1; 1; 1), B (2; 0; 2), C (1-; -1; 0), D (0; 3; 4). Trên các cạnh AB, AC, AD lần lượt lấy các điểm B', C', D' thỏa $\frac{AB}{AB'}\;+\;\frac{AC}{AC'}\;+\;\frac{AD}{AD'}\;=\;4$ Viết phương trình mặt phẳng (B' C' D') biết tứ diện AB'C'D' có thể tích nhỏ nhất?
- A.
  16x + 40y + 44z - 39 = 0
- B.
  16x - 40y - 44z + 39 = 0
- C.
  16x - 40y - 44z - 39 = 0
- D.
  16x + 40y - 44z + 39 = 0
Câu 23: Nhận biết
Câu 23:

Ông An gửi tiết kiệm 50 triệu đồng vào ngân hàng với kỳ hạn 3 tháng, lãi suất 8,4 % một năm theo hình thức lãi kép. Ông gửi được đúng 3 kỳ hạn thì ngân hàng thay đổi lãi suất, ông gửi tiếp 12 tháng nữa với kỳ hạn như cũ và lãi suất trong thời gian này là 12% một năm thì ông rút tiền về. Số tiền ông An nhận được cả gốc lẫn lãi là: (làm tròn đến chữ số hàng đơn vị)
- A.
  62255910 đồng
- B.
  59895767 đồng
- C. 59993756 đồng
- D. 63545193 đồng
Câu 24: Nhận biết
Câu 24:

Một chất điểm chuyển động theo phương trình S = -t³ + 3t² - 2, trong đó t tính bằng giây và S tính theo mét. Chuyển động có vận tốc lớn nhất là
- A.
  1 m/s
- B.
  B . 4 m/s
- C. 3 m/s
- D. 2 m/s
Câu 25: Nhận biết
Câu 25:

Elip có một tiêu điểm F (-2;0) và tích độ dài trục lớn với trục bé bằng $12\sqrt{5}$ . Phương trình chính tắc của elip là:
- A.
  $\frac{x^{2} }{9} + \frac{y^{2}}{5} = 1$
- B.
  $\frac{x^{2} }{45} + \frac{y^{2}}{16} = 1$
- C.
  $\frac{x^{2} }{144} + \frac{y^{2}}{5} = 1$
- D.
  $\frac{x^{2} }{36} + \frac{y^{2}}{20} = 1$
Câu 26: Nhận biết
Câu 26:

Cho số thực x > 0. Tìm hệ số của số hạng không chứa x trong khai triển nhị thức Newton của biểu thức $(2x + \frac{1}{x})^{n}$ biết rằng $C_{n}^{k - 2} + 2C_{n}^{k - 1} + C_{n}^{k} = \frac{2018C_{n + 1}^{k - 1} }{k}$ trong đó k, n là những số nguyên dương thỏa mãn 2 $\leq$ k $\leq$ n
- A.
  $C_{2016}^{1008}$
- B.
  $C_{2018}^{1009} . 2^{1009}$
- C.
  $C_{2016}^{1008} . 2^{1008}$
- D.
  $C_{2014}^{1007} . 2^{1007}$
Câu 27: Nhận biết
Câu 27:

Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật ABCD có điểm C thuộc đường thẳng d: 2x + y + 5 = 0 và điểm A(-4;8) Gọi M đối xứng với B qua C, điểm N(5;-4) là hình chiếu vuông góc của B lên đường thẳng MD. Biết tọa độ C(m;n), giá trị của m-n là:
- A.
  6
- B.
  -6
- C.
  8
- D.
  7
Câu 28: Nhận biết
Câu 28:

Cho hàm số y = f(x) có bảng biến thiên như sau. Hàm số $y = f(\begin{vmatrix} x-3 \end{vmatrix} )$ có bao nhiêu điểm cực trị?
- A.
  5
- B.
  6
- C.
  3
- D.
  1
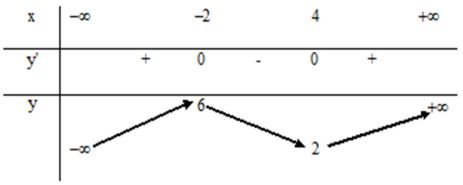
Câu 29: Nhận biết
Câu 29:

Tìm tất cả các giá trị của m để hàm số $y = log_{2018} (2018^{x} -x-\frac{x^{2} }{2} -m)$ xác định với mọi thuộc [0;+ $\infty$ )
- A.
  m > 9
- B.
  m < 1
- C.
  0 < m < 1
- D.
  m < 2
Câu 30: Nhận biết
Câu 30:

Cho khai triển (x² + x - 6)ⁿ = a₀ + a₁x + a₂x² + ...+ a_2nx²ⁿ biết a₀ + a₁ + a₂ +...+ a_2n = 1048576 khi đó a₁bằng:
- A.
  – 107769600
- B.
  – 100776960
- C.
  – 100770696
- D.
  – 100707696
Câu 31: Nhận biết
Câu 31:

Gọi x, y là các số thực dương thỏa mãn điều kiện log₉x = log₄(x+y) và $\frac{x}{y} = \frac{-a + \sqrt{b} }{2}$ , với a,b là hai số nguyên dương. Tính a + b
- A.
  11
- B.
  4
- C.
  6
- D.
  8
Câu 32: Nhận biết
Câu 32:

Có bao nhiêu số thực a để $\int_{1}^{0} \frac{x}{a + x2} dx = 1$
- A.
  2
- B.
  1
- C.
  0
- D.
  3
Câu 33: Nhận biết
Câu 33:

Cho hình chóp S. ABCD có đáy ABCD là hình vuông và tam giác SAB đều nằm trên mặt phẳng vuông góc với đáy. Biết khoảng cách giữa hai đường thẳng SA và BD bằng $\sqrt{21}$ . Hãy cho biết cạnh đáy bằng bao nhiêu?
- A.
  $\sqrt{21}$
- B.
  21
- C.
  7 $\sqrt{3}$
- D.
  7
Câu 34: Nhận biết
Câu 34:

Giả sử hàm số y = f(x) liên tục, nhận giá trị dương trên (0;+ $\infty$ ) và thỏa mãn $f(1) = e, f(x) = f'(x) \sqrt{3x + 1}$ , với mọi x > 0. Mệnh đề nào sau đây đúng?
- A.
  10 < f(5) < 11
- B.
  4 < f(5) < 5
- C.
  11 < f(5) < 12
- D.
  3 < f(5) < 4
Câu 35: Nhận biết
Câu 35:

Cho hai số phức z₁, z₂ thoả mãn đồng thời hai điều kiện sau $\begin{vmatrix} z-1 \end{vmatrix} = \sqrt{34} , \begin{vmatrix} z + 1 + mi \end{vmatrix} = \begin{vmatrix} z + m + 2i \end{vmatrix}$ (trong đó m là số thực) và sao cho $\begin{vmatrix} z_{1} - z_{2} \end{vmatrix}$ lớn nhất. Khi đó giá trị của $\begin{vmatrix} z_{1} + z_{2} \end{vmatrix}$ bằng
- A.
  $\sqrt{2}$
- B.
  10
- C.
  2
- D.
  $\sqrt{130}$
Câu 36: Nhận biết
Câu 36:

Lăng trụ tam giác ABC.A'B'C' có đáy tam giác đều cạnh a, góc giữa cạnh bên và mặt đáy bằng 30⁰. Hình chiếu A' lên (ABC) là trung điểm I của BC. Thể tích khối lăng trụ là
- A.
  $\frac{a^{2} \sqrt{3} }{2}$
- B.
  $\frac{a^{2} \sqrt{3} }{12}$
- C.
  $\frac{a^{2} \sqrt{3} }{8}$
- D.
  $\frac{a^{2} \sqrt{3} }{6}$
Câu 37: Nhận biết
Câu 37:

Có bao nhiêu cặp điểm trên đồ thị hàm số y = -x³ + x² + 3x - 4 đối xứng nhau qua gốc tọa độ
- A.
  0
- B.
  3
- C.
  1
- D.
  2
Câu 38: Nhận biết
Câu 38:

Cho khối chóp O.ABC. Trên ba cạnh OA, OB, OC lần lượt lấy ba điểm A', B', C' sao cho 2OA' = OA, 4OB' = OB, 3OC' = OC. Tính tỉ số $\frac{V_{O.A'B'C'} }{V_{O.ABC}}$
- A.
  $\frac{1}{24}$
- B.
  $\frac{1}{16}$
- C.
  $\frac{1}{12}$
- D.
  $\frac{1}{32}$
Câu 39: Nhận biết
Câu 39:

Gọi a, b lần lượt là các nghiệm dương của phương trình x²⁰¹⁸ + x²⁰¹⁷ + x²⁰¹⁶+ ... + x - 1 = 0 và x²⁰¹⁹ + x²⁰¹⁸ + x²⁰¹⁷ + ... + x - 1 = 0. Khẳng định nào sau đây là đúng
- A.
  b > a + 1
- B.
  a > b + 1
- C.
  alnb > blna
- D.
  blna > alnb
Câu 40: Nhận biết
Câu 40:

Gọi S là tập các số tự nhiên có 5 chữ số. Chọn ngẫu nhiên từ tập S một phần tử. Xác suất để số chọn được chia hết cho 7 và có số hàng đơn vị là 1
- A.
  $\frac{157}{11250}$
- B.
  $\frac{643}{45000}$
- C.
  $\frac{1357}{52133}$
- D.
  $\frac{11}{23576}$
Câu 41: Nhận biết
Câu 41:

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = 8, BC = 6. Biết SA = 6 và SA vuông góc với mặt phẳng (ABC) . Tính thể tích hình cầu có tâm thuộc phần không gian bên trong của hình chóp và tiếp xúc với tất cả các mặt của hình chóp S.ABC.
- A.
  $\frac{16}{9} \pi$
- B.
  $\frac{625}{81} \pi$
- C.
  $\frac{256}{81} \pi$
- D.
  $\frac{25}{9} \pi$
Câu 42: Nhận biết
Câu 42:

Có bao nhiêu giá trị nguyên của tham số m để hàm số y = x¹² + (m-5) x⁷ + (m² - 25) x⁶ + 1.

đạt cực đại tại x = 0?
- A.
  8
- B.
  9
- C.
  Vô số
- D.
  10
Câu 43: Nhận biết
Câu 43:

Cho phương trình ax³ - x² + bx - 1 = 0 có ba nghiệm dương. Khi $P = \frac{5a^{2} - 3ab + 2}{a^{2} (b - a)}$

đạt giá trị nhỏ nhất thì giá trị của $T = \frac{1}{a^{2} } + 3b^{2}$ là
- A.
  45
- B.
  100
- C.
  25
- D.
  30
Câu 44: Nhận biết
Câu 44:

Có bao nhiêu số nguyên m không nhỏ hơn – 2018 để bất phương trình $m(\sqrt{x^{2}-2x + 2 + 1) } + x(2-x)\leq 0$ có nghiệm $x \in \begin{bmatrix} 0;1+\sqrt{3} \end{bmatrix}$
- A.
  2018
- B.
  2019
- C.
  2017
- D.
  2020
Câu 45: Nhận biết
Câu 45:

Có bao nhiêu giá trị nguyên của tham số m để phương trình $log_{2+\sqrt{5} } (2x^{2} -x-4m^{2} ) + log\sqrt{\sqrt{5} -2} \sqrt{x^{2} +mx-2m^{2} } = 0$

có hai nghiệm phân biệt x1, x2 thỏa mãn $x_{1}^{2} + x_{2}^{2} = 3$
- A.
  1
- B.
  0
- C.
  3
- D.
  2
Câu 46: Nhận biết
Câu 46:

Cho hình hộp chữ nhật ABCD.A'B'C'D' đáy là hình vuông cạnh bằng 1, cạnh bên AA’ = 2. Gọi (P) làmặt phẳng chứa CD' và tạo với mặt phẳng (BDD’B’) một góc $\varphi$ nhỏ nhất, cos $\varphi$ bằng
- A.
  $\frac{\sqrt{10} }{5}$
- B.
  $\frac{\sqrt{6} }{4}$
- C.
  $\frac{\sqrt{3} }{2}$
- D.
  $\frac{3\sqrt{10} }{10}$
Câu 47: Nhận biết
Câu 47:

Xét tất cả các tam thức bậc hai: f(x) = ax² + bx + c $\geq$ 0, $\forall x\in \mathbb{R} , a < b$

Giá trị nhỏ nhất của biểu thức: $A = \frac{a + b + c}{b - a}$ là
- A.
  2
- B.
  7
- C.
  4
- D.
  3
Câu 48: Nhận biết
Câu 48:

Trong không gian Oxyz, cho mặt cầu (S): x² + (y - 1)² + (z + 1)² = 1 và đường thẳng $d:\;\left\{\begin{array}{l}x\;=\;2\;+\;t\\y\;=\;t\\z\;=\;-t\end{array}\right.$ Hai mặt phẳng (P), (Q) chưa d, tiếp xúc với (S) tại T và T’. Điểm H(a;b;c) là trung điểm đoạn TT’, giá trị của biểu thức T = a + b + c là
- A.
  0
- B.
  $\frac{1}{3}$
- C.
  $\frac{2}{3}$
- D.
  1
Câu 49: Nhận biết
Câu 49:

Tìm tất cả các giá trị của tham số m để đường thẳng y = -2x + m cắt đồ thị (H) của hàm số y = $\frac{2x + 3}{x + 2}$ tại hai điểm A, B phân biệt sao cho $P = k_{1}^{2018} + k_{2}^{2018}$ đạt giá trị nhỏ nhất với k₁, k₂ là hệ số góc của tiếp tuyến tại A, B của đồ thị (H).
- A.
  m = -3
- B.
  m = 3
- C.
  m = -2
- D.
  m = 2
Câu 50: Nhận biết
Câu 50:

Cho hình chóp S.ABCD, đáy ABCD là hình bình hành có AB = 4, Bc = 3, SA = SB = SC = SD = 6. K là hình chiếu vuông góc của B xuống AC . Tính độ dài d đoạn vuông góc chung của SA và BK
- A.
  $\frac{\sqrt{119} }{11}$
- B.
  $\frac{4\sqrt{229} }{13}$
- C.
  $\frac{\sqrt{259} }{5}$
- D.
  $\frac{4\sqrt{119} }{15}$

Chia sẻ bởi:
Nguyễn Linh An

110

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!

Sắp xếp theo

Xóa Đăng nhập để Gửi

Mầm non

Lớp 1

Lớp 2

Lớp 3

Lớp 4

Lớp 5

Lớp 6

Lớp 7

Lớp 8

Lớp 9

Lớp 10

Lớp 11

Lớp 12

Thi vào lớp 6

Thi vào lớp 10

Thi Tốt Nghiệp THPT

Đánh Giá Năng Lực

Khóa Học Trực Tuyến

Hỏi bài

Trắc nghiệm Online

Tiếng Anh

Thư viện Học liệu

Bài tập Cuối tuần

Bài tập Hàng ngày

Thư viện Đề thi

Giáo án - Bài giảng

Tất cả danh mục

Đề kiểm tra năng lực giáo viên môn Toán trường THPT Gia Bình, Bắc Ninh

Chúc mừng Bạn đã hoàn thành bài!

Trắc nghiệm Online

Trắc nghiệm Lớp 12

Trắc nghiệm Lớp 12

Trắc nghiệm Tin học 12 bài 11

Trắc nghiệm Tin 12 bài 13

Trắc nghiệm Lịch sử lớp 12 bài 21 phần 1

Trắc nghiệm Lịch sử lớp 12 bài 1 phần 1 Online

Trắc nghiệm môn GDCD lớp 12 bài 1 Online

Trắc nghiệm Lịch sử lớp 12 bài 3 - Phần 1