Đề thi tham khảo vào lớp 10 môn Toán Phòng GD&ĐT Quận 12 năm học 2019 - 2020
Đề thi tham khảo vào lớp 10 môn Toán 2019 TPHCM có đáp án
VnDoc - Tải tài liệu, văn bản pháp luật, biểu mẫu miễn phí
VnDoc - Tải tài liệu, văn bản pháp luật, biểu mẫu miễn phí
ỦY BAN NHÂN DÂN QUẬN 12
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO QUẬN 12
ĐỀ THAM KHẢO THI TUYỂN SINH LỚP 10 NĂM HỌC 2019 – 2020
MÔN THI : TOÁN (120 phút)
ĐỀ 1
Ro 1 (1 o) : Cho pt:
2
2 5 2 5 0x x
có 2 nghiệm
1 2
;x x
.
Tính giá trị
2
1 2 1 2
2 5M x x x x
Ro 2:(1ͥ꿸 o) Cho hàm số (P):
2
4
x
y
và (D):
2
2
x
y
a) Vẽ đồ thị của 2 hàm số trên cùng một hệ trục toạ độ
b) Tìm tọa độ giao điểm của (P) và (D).
Ro : (1 o) Cho tam giác ABC vuông tại A có
5 3AB cm
;
3 3 1AC cm
và
đường trung tuyến AM. Tính độ dài AM.
Ro : (1 o) Một thửa đất hình chữ nhật có chiều dài là
32m và chiều rộng là 24m. Người ta định làm một vườn
cây cảnh có con đường đi xung quanh, có bề rộng x(m)
(hình vẽ bên). Hỏi bề rộng của mặt đường là bao nhiêu để
diện tích phần đất còn lại là
2
560m
.
Ro 꿸: (1ͥ꿸 o) Cho phương trình
2 2
3 2 2 5 0x m x m m
(1) (x là ẩn số)
a) Chứng minh phương trình luôn có 2 nghiệm phân biệt với mọi giá trị m
b) Gọi
1 2
,x x
là nghiệm của pt trên. Tìm m để phương trình có hai nghiệm
thỏa
1 2 1 2 1 1 2
(2 ) 13x x x x x x x
Ro 6(1 o) Công ty TQK bỏ tiền để được đầu tư 1 trong 2 dự án như sau:
Dự án 1: Chi phí đầu tư 200 000 000 đồng và đem lại lợi nhuận 290 000 000 đồng trong
vòng 2 năm.
Dự án 2: Chi phí đầu tư 250 000 000 đồng và đem lại lợi nhuận 345 000 000 đồng trong
vòng 2 năm.
Với lãi suất thịnh hành 8% một năm ở ngân hàng. Em hãy tính xem nên chọn dự án nào
đầu tư có lợi nhuận cao hơn.
Ro : ( o) Cho điểm A nằm ngoài đường tròn (O; R). Từ A, vẽ 2 tiếp tuyến AB,
AC và cát tuyến ADE của (O) sao cho O nằm trong góc EAC.
a/ Chứng mimh:
OA BC
tại H và AB.AC = AD.AE
b/ Vẽ tiếp tuyến tại E của (O; R) cắt CB ở T. Chứng minh: TD là tiếp tuyến của (O)
c/ Gọi K là giao điểm của DE và BC và F là trung điểm của DE.
Chứng minh: AD.KE = AE.KD và KD.KE = KA.KF
VnDoc - Tải tài liệu, văn bản pháp luật, biểu mẫu miễn phí
VnDoc - Tải tài liệu, văn bản pháp luật, biểu mẫu miễn phí
Hết.
ĐÁP ÁN:
Bài 1/ Theo định lý Vi-ét ta có
1 2
5 2 5
;
2 2
S x x P
(0,5đ)
2
1 2 1 2
2
2
2 5
5 2 5 5
4 2 5 4 2 5
2 2 2
25 5 51
4 2 5 2 5
4 2 4
M x x x x
M S P S
M
Bài 2/
a/ Lập bảng giá trị mỗi hàm số (0,25đ) + Vẽ đúng mỗi ĐTHS (0,25đ)
b/ Phương trình hoành độ giao điểm của (P) và (d) là
2
2
4 2
x x
Giải ra: (2;1) và (- 4;- 4) (0,25đ)
Bài 3/ Tính được
3 1BC
cm (0,5đ). Tính ra
3 1
2
AM cm
(0,5đ)
Bài 4/ Biết x(m) là bề rộng con đường (x >0 và x < 24)
Chiều dài của hình chữ nhật còn lại là 32 – 2x (m)
Chiều rộng của hình chữ nhật còn lại là 24 – 2x (m) (0,25đ)
Theo đề bài ta có:
(32 2 ).(24 2 ) 560x x
(0,25đ)
Giải ra: x = 26 (loại) và x = 2 (nhận) (0,25đ)
Vậy bề rộng của mặt đường là 2m.
Bài 5/
a/
2
4 24m m
(0,25đ)
2
( 2) 20 0m
với mọi x (0,25đ)
Vậy pt luôn luôn có 2 nghiệm phân biệt với mọi m. (0,25đ)
b/ Theo định lý Vi –ét ta có;
2
1 2
3 2; 2 5S x x m P m m
(0,25đ)
0,25 đ
0,25 đ
0,25 đ
VnDoc - Tải tài liệu, văn bản pháp luật, biểu mẫu miễn phí
VnDoc - Tải tài liệu, văn bản pháp luật, biểu mẫu miễn phí
1 2 1 2 1 1 2
2 2 2
1 2 1 1 2
2 2
1 2 1 2
2
2 2
2 2
2
(2 ) 13
2 13
13 0
3 13 0
(3 2) 3(2 5) 13 0
9 12 4 6 3 15 13 0
3 9 6 0
x x x x x x x
x x x x x
x x x x
S P
m m m
m m m m
m m
Giải ra m = 2 hoặc m = 1 (0,25đ)
Bài 6/
Dự án 1:
Tính ra vốn và lời dùng để gửi ngân hàng sau 2 năm là 233280000 đồng (0,25đ)
Số tiền lời so với ngân hàng trong 2 năm là
290000000 233280000 56720000
đồng (0,25đ)
Dự án 2:
Tính ra vốn và lời dùng để gửi ngân hàng sau 2 năm là 291600000 đồng
Số tiền lời so với ngân hàng trong 2 năm là
345000000 291600000 53400000
đồng (0,25đ)
Vậy chọn dự án 1 đầu tư có lợi nhuận cao hơn. (0,25đ)
Bài 7/
a/ Chứng minh: OA là đường trung trực
của BC (0,25 đ)
OA BC
(0,25đ)
Chứng minh:
~ ( . )ABD AEB g g
(0,25đ)
2
.
AB AD
AB AD AE
AE AB
Mà AB=AC (t/c 2 tiếp tuyến cắt nhau)
=>AB.AC=AD.AE (0,25đ)
b/ Chứng minh: tứ giác OHDE và
OHTE nội tiếp (0,25đ + 0,25đ)
=> O; H; D; T; E cùng thuộc một
đường tròn (0,25đ)
=> góc ODT = góc OHT = 90
0
=>
TD OD
=> TD là tiếp tuyến của đường tròn (O; R) (0,25đ)
c/ Chứng minh: HK là tia phân giác của
HDE
(0,25đ)
KD HD
KE HE
0,25 đ
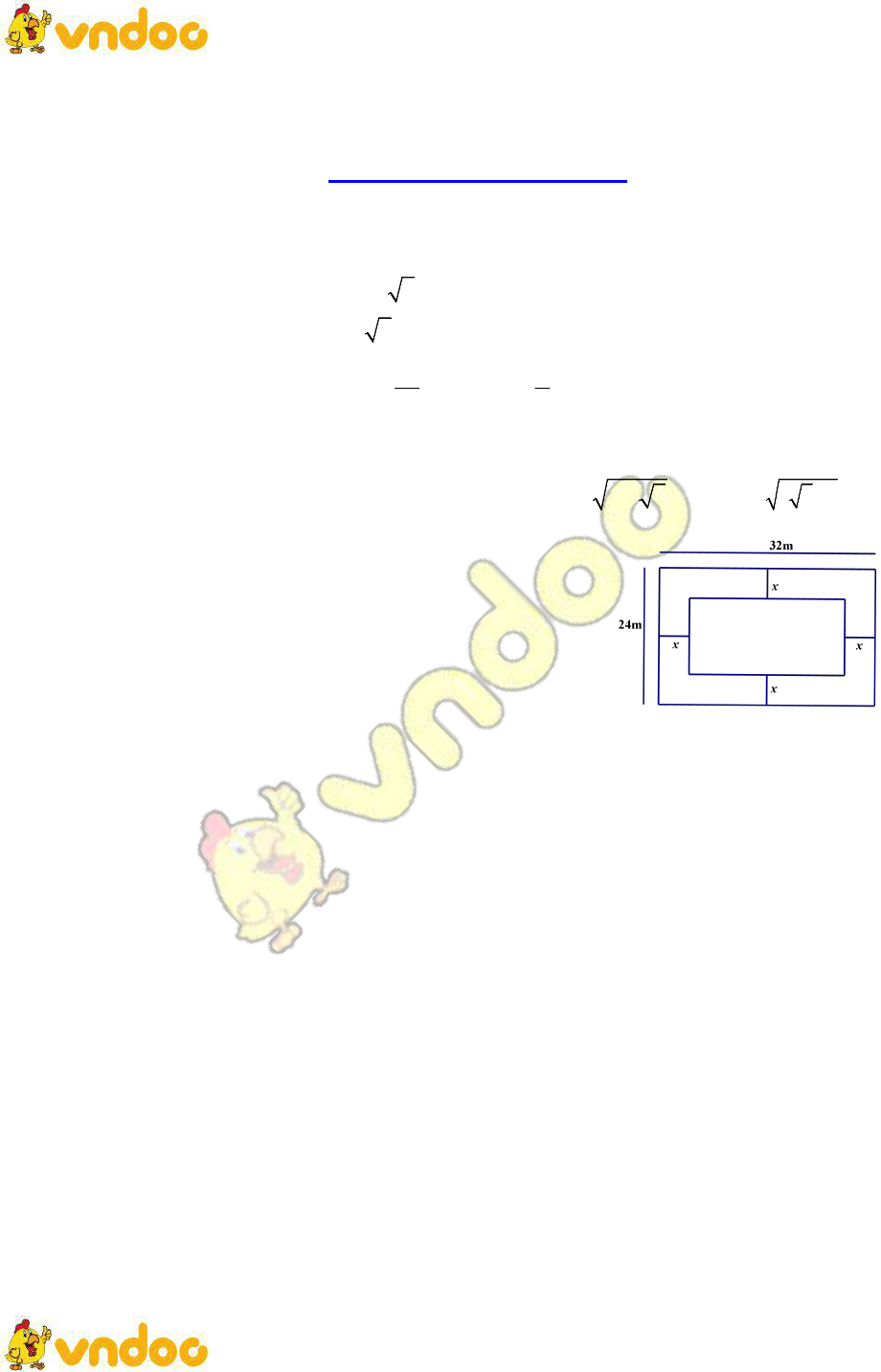
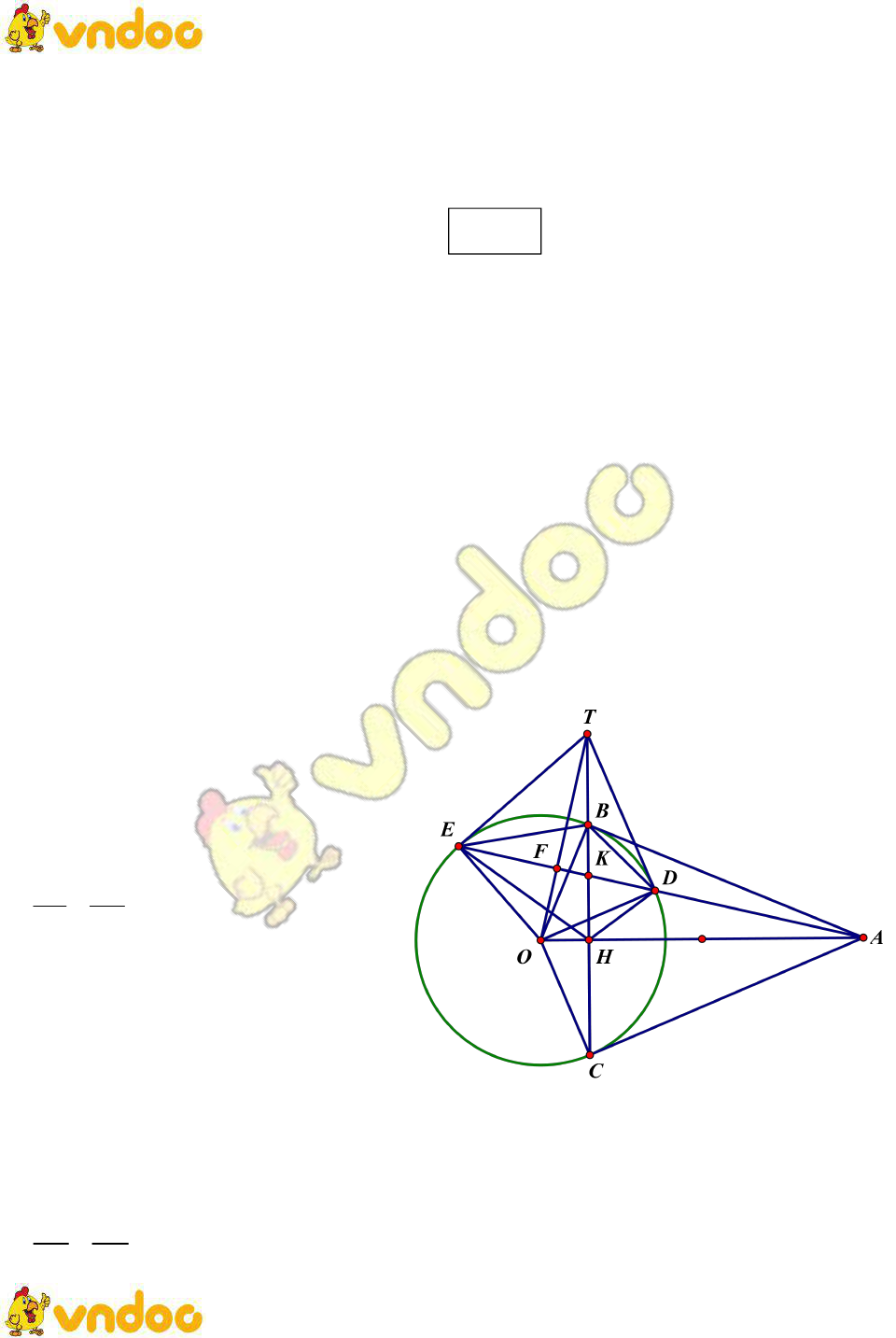
Đề thi tham khảo vào lớp 10 môn Toán Phòng GD&ĐT Quận 12 năm 2019
Đề thi tham khảo vào lớp 10 môn Toán Phòng GD&ĐT Quận 12 năm học 2019 - 2020 do thư viện đề thi VnDoc.com sưu tầm. Đây là đề thi tham khảo vào lớp 10 môn Toán dành cho các bạn học sinh ôn tập, củng cố kiến thức, rèn luyện kĩ năng làm bài Toán. Mời các bạn cùng tham khảo
- Đề thi tham khảo vào lớp 10 môn Toán Phòng GD&ĐT Quận 4 năm học 2019 - 2020
- Đề thi tham khảo vào lớp 10 môn Toán Phòng GD&ĐT Quận 5 năm học 2019 - 2020
- Đề thi tham khảo vào lớp 10 môn Toán Phòng GD&ĐT Quận 6 năm học 2019 - 2020
- Đề thi tham khảo vào lớp 10 môn Toán Phòng GD&ĐT Quận 8 năm học 2019 - 2020
- Đề thi tham khảo vào lớp 10 môn Toán Phòng GD&ĐT Quận 9 năm học 2019 - 2020
- Đề thi tham khảo vào lớp 10 môn Toán Phòng GD&ĐT Quận 11 năm học 2019 - 2020
.............................................
Ngoài Đề thi tham khảo vào lớp 10 môn Toán Phòng GD&ĐT Quận 12 năm học 2019 - 2020. Mời các bạn học sinh còn có thể tham khảo các đề thi học kì 2 lớp 9 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề Thi vào lớp 10 năm 2019 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt
