Đề thi thử vào lớp 10 môn Toán Trường Đại học Sư Phạm Hà Nội năm học 2021 - 2022 (vòng 2)
Đề thi tuyển sinh lớp 10 môn Toán có đáp án
TRƯỜNG ĐẠI HỌC SƯ PHẠM HÀ NỘI
TRƯỜNG THPT CHUYÊN
VÒNG 2
KIỂM TRA KHẢO SÁT THI VÀO 10
NĂM HỌC 2021 - 2022
MÔN: TOÁN
Thời gian làm bài 90 phút
Câu 1. (2,0 điểm). Cho
, ,
x y z
là các số thực dương thỏa mãn
( ) 1
xyz x y z
. Chứng minh rằng
2 2 2
2 2 2
1 1 1
( )( )( )
x y z x y y z z x
y z z
.
Câu 2. (3,0 điểm).
1) Cho hai số thực không âm
,
a b
thỏa mãn
2
a b . Chứng minh
2 2 2
2 2 2
( )
1 1 1 ( )
a b a b
a b a b
2) Tìm tất cả các số nguyên tố
,
p q
thỏa mãn
2 1
p q
p q q p
Câu 3. (1,0 điểm). Cho tập hợp
S
có các phần tử là các số thực,
S
chứa tất cả các số nguyên và
đóng đối với phép cộng và nhân, tức là với hai phần tử bất kỳ
,
x y
thuộc
S
ta có
x y
và
.
x y
đều
thuộc
S
. Biết rằng:
2020 2021
thuộc
S
, chứng minh
2020 2021
thuộc S.
Câu 4 (3,0 điểm). Cho đường tròn
O
và dây cung
AB
cố định, không là đường kính. Điểm
M
thay đổi
trên đoạn
AB
sao cho
,
M A M B
và
AM MB
. Đường thẳng
vuông góc với
OM
tại
M
,
cắt đường tròn
O
tại
P
và
Q
. Đường tròn đường kính
AM
cắt đường tròn
O
tại điểm thứ hai
K K A
và cắt đoạn thẳng
PQ
tại điểm thứ hai
D D M
. Gọi
S
là giao điểm của
AK
với
PQ
,
F
là giao điểm của
SB
với dường tròn
O F B
và
H
là trực tâm của tam giác
APQ
.
Chứng minh
a) Tứ giác
BMDF
nội tiếp.
b) Các điểm
M
,
H
,
K
thẳng hàng.
c) Đường thẳng
HF
luôn đi qua một điểm cố định khi
M
thay đổi trên đoạn
AB
.
Câu 5. (1,0 điểm). Cho tập hợp
1;2;....;2022
X
.
a) Xét tập con
M
của
X
gồm 1012 phần tử. Chứng minh rằng luôn có hai phần tử
,
a b
của
M
mà
a b
và
b
là bội của
a
.
b) Tìm số nguyên dương
n
lớn nhất sao cho với mọi tập con
A
của
X
có 1348 phần tử thì trong
A
có ít nhất
n
cặp
;
a b
mà
a b
và
b
là bội của
a
.
---HẾT---
HƯỚNG DẪN
Câu 1. (2,0 điểm). Cho
, ,
x y z
là các số thực dương thỏa mãn
( ) 1
xyz x y z
. Chứng minh rằng
2 2 2
2 2 2
1 1 1
( )( )( )
x y z x y y z z x
y z z
.
Hướng dẫn
Ta có
2 2 2 2
2
2 2 2 2
1 1 ( ) ( )( )
x y x y xyz x y z xy z x z y
x
y y y y
Tương tự, ta có:
2 2
2 2 2 2
1 ( )( ) 1 ( )( )
;
yz x y x z xz y x y z
y z
z z x x
Do đó
2 2 2
2 2 2
1 1 1
( )( )( )
x y z x y y z z x
y z z
(đpcm).
Câu 2. (3,0 điểm).
1) Cho hai số thực không âm
,
a b
thỏa mãn
2
a b . Chứng minh
2 2 2
2 2 2
( )
1 1 1 ( )
a b a b
a b a b
2) Tìm tất cả các số nguyên tố
,
p q
thỏa mãn
2 1
p q
p q q p
Hướng dẫn
Nhận xét: điểm rơi của bài toán ta thử kiểm tra thấy rằng tại cả trung tâm và tại biên bài toán đều
đúng nên đây là bài toán khá chặt nếu sử dụng B.Đ.T cổ điển trong phòng thi sẽ rất tốn thời gian để
tìm hướng giải. Giải pháp theo tôi là sử dụng phương pháp biến đổi tương đương để không làm giảm
độ mạnh của bất đẳng thức.
Do
, 0
a b
nên
2 2 2
1 0; 1 0; 2 ( ) 0
a b a b
. Khi đó, ta cần phải chứng minh :
2 2 2 2 2 2 2 2 2 2
( 2 )[1 ( ) ] ( 1)( )
a b a b a b a b a b a b
Xét hiệu:
2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2
2 2 2 2 2 2 2 2
2 2 2 2
( 1)( ) ( 2 )[1 ( ) ]
( 2 )( ) (1 )( ) ( 2 )( ) ( 2 )
(1 )( ) ( 2 )
( ) ( ) ( ) 2
2 ( ) 2
M a b a b a b a b a b a b
M a b a b a b a b a b a b a b a b a b a b
M a b a b a b a b
M a b a b a b a b a b
M ab a b a b a b
2 2
[2 ( ) 2 ]ab ab a b ab
Do
2
2 2
2
2 ( )
2 [( ) 2 2 ] ( ) 0
( ) 2
a b
a b M ab a b ab ab ab a b dpcm
a b
Dấu bằng xảy ra khi
0
0; 2
0
2; 0
0
2
, 0; 2
2
a
a b
b
a b
a b
a b
a b a b
Cách 2: Ta có:
2 2
1
4 ( ) 2 & ( ) 2
2
ab a b ab a b
Bất đẳng thức được viết lại :
2 2 2 2 2 2
2 2 2 2 2 2
2 2 2
2 2
2 2 2
1 1 1 1 1 1
1 1 1 1
1 1 1 ( ) 1 1 1 ( )
2 (1 ) 1
(1 )(1 ) 1 ( )
1 1
(1 )(1 ) 1 ( )
a b a b a b a b
a b a b a b
a b a b
a b
a b a b
2 2 2 2 2
2 2 2 2 2 2 2 2 2 2
2 2 2 2 2
2
(1 )[1 ( ) ] (1 )(1 )
1 ( ) ( ) 1
2 2 ( ) 0
[2 2 ( ) ] 0
a b a b a b
a b a b a b a b a b a b
ab a b a b a b
ab ab ab a b
Ta có:
2
2
2 2 ( ) 0
1 1
2 ( ) 2. .2 2 0
2 2
0
ab ab a b
ab ab a b VT dpcm
ab
.
Dấu bằng xảy ra khi
1
0; 2 2; 0
2
a b a b a b
Cách 3:
Biến đổi B.Đ.T cần chứng minh về dạng
2 2
2 2
2 2
1 ( ) ( )
1 1
a b
a b a b
a b
2 2 2 2 2 2
2
2 2
(1 2 ) (1 2 )
( )
1 1
a a ab b b a ab b
a b
a b
Áp dụng B.Đ.T Cauchy Schwarz, ta có
2 2 2 2 2 2 2
2 2
2 2 2
2 2 2 2
2 2
2 2 2 2
2 2
2
2 2
(1 2 ) (2 ) 2 (2 )
1 1 2 2
2 (2 ) 2 (2 )
( ) 2 2 ( )
2 (2 ) 4 1
9 2 ( )
a a ab b a ab b a ab b
a a
a a a
a ab b a ab b
a a
a b a a a b a b
a ab b
a
a a b a b
Bằng cách tương tự, ta có:
2 2 2 2 2
2
2 2 2
(1 2 ) 2 (2 ) 4 1
1 9 2 ( )
b a ab b b ab a
b
b b a b a b
Do đó, ta có:
2 2 2 2
2 2 2
2 2 2 2
2 2 2
1 4 ( )
1 ( ) 12
1 1 9
2 ( ) .
a b ab a ab b
a b a b ab
a b a b
a b ab a b
Câu 3. (1,0 điểm). Cho tập hợp
S
có các phần tử là các số thực,
S
chứa tất cả các số nguyên và
đóng đối với phép cộng và nhân, tức là với hai phần tử bất kỳ
,
x y
thuộc
S
ta có
x y
và
.
x y
đều
thuộc
S
. Biết rằng:
2020 2021
thuộc
S
, chứng minh
2020 2021
thuộc S.
Hướng dẫn
Phân tích:
Hai biểu thức
2020 2021
và
2020 2021
có dạng “liên hợp” nên có thể dẫn chúng ta đến
suy nghĩ xét tích 2 biểu thức này. Ta có:
( 2020 2021)( 2020 2021) 1
Ta lại chú ý đến sự ngược dấu của hai biểu thức
a b
và
–
a b
, từ đó ta liên hệ đến:
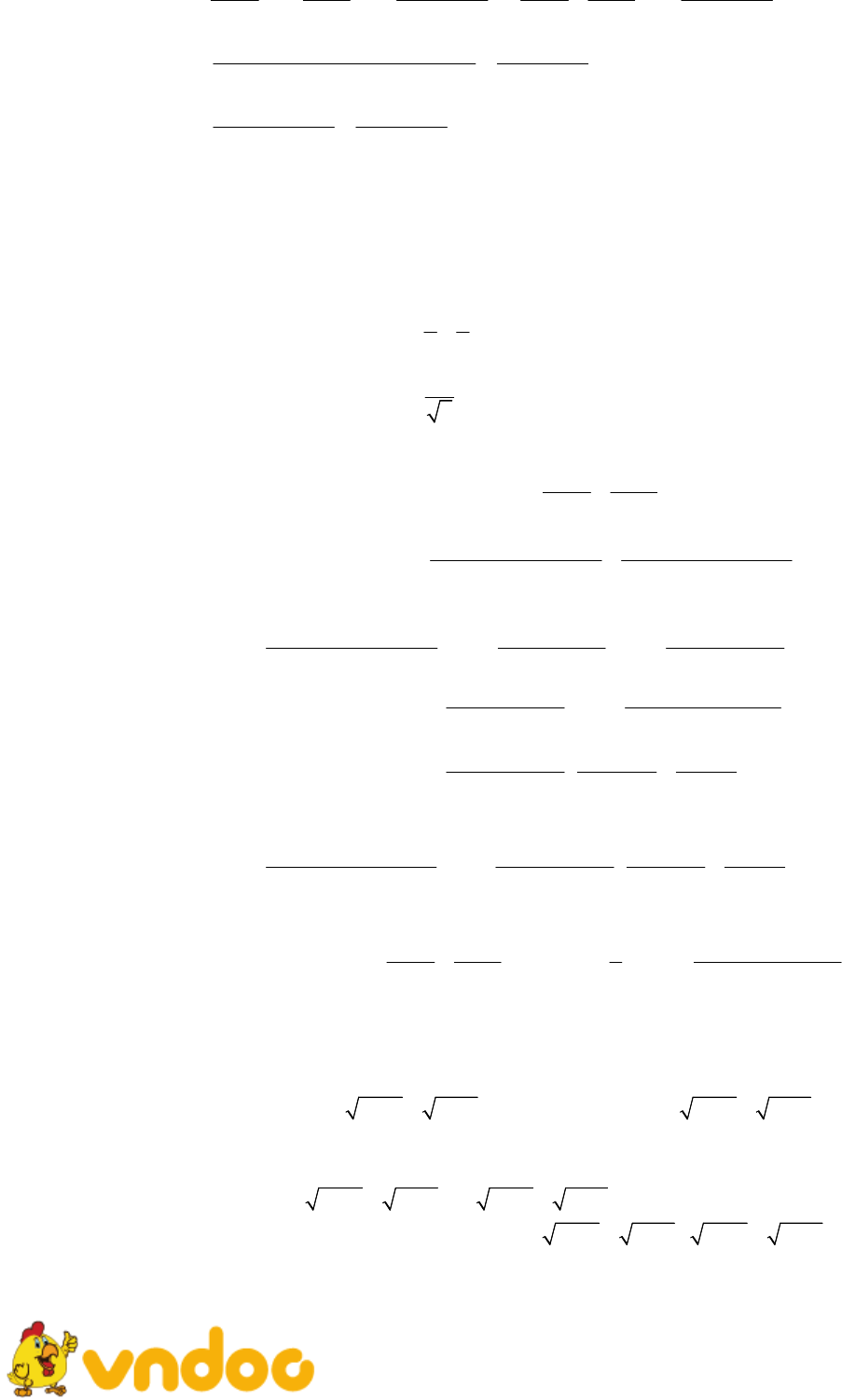
Đề thi thử vào lớp 10 môn Toán Trường Đại học Sư Phạm Hà Nội năm học 2021
Đề thi thử vào lớp 10 môn Toán Trường Đại học Sư Phạm Hà Nội năm học 2021 - 2022 (vòng 2) được VnDoc sưu tầm và đăng tải. Đây là đề thi tham khảo vào lớp 10 môn Toán dành cho các bạn học sinh ôn tập, củng cố kiến thức, rèn luyện kĩ năng làm bài Toán. Mời các bạn cùng tham khảo
- Tổng hợp đề thi thử vào lớp 10 môn Toán cả nước năm 2021
- Tổng hợp đề thi học kì 2 Văn 9 cả nước năm 2020 - 2021
- Tổng hợp đề thi vào lớp 10 môn Toán Sở GD&ĐT Thanh Hóa
Ngoài ra, VnDoc.com đã thành lập group chia sẻ tài liệu học tập THCS miễn phí trên Facebook: Tài liệu học tập lớp 9. Mời các bạn học sinh tham gia nhóm, để có thể nhận được những tài liệu mới nhất.
Đề thi thử vào lớp 10 môn Toán Trường Đại học Sư Phạm Hà Nội năm học 2021 - 2022 (vòng 2) được VnDoc chia sẻ trên đây với 5 câu hỏi tự luận với thời gian 120 phút, giúp các bạn học sinh có thêm tài liệu ôn tập chuẩn bị tốt cho kì thi sắp tới. Ngoài đề thi thử trên đây các bạn tham khảo các đề của các tỉnh khác nữa nhé
- Tổng hợp đề thi vào lớp 10 được tải nhiều nhất
- Bộ đề thi vào lớp 10 môn Toán
- Bộ đề thi tuyển sinh lớp 10 môn toán năm 2020 - 2021
- Đề thi thử vào lớp 10 môn Toán Trường THCS Thạch Bàn năm 2021
- Đề thi thử vào lớp 10 môn Toán Trường THCS Quán Hành, Nghệ An năm 2021
- Đề thi thử vào lớp 10 môn Toán Trường THPT Lam Kinh, Thanh Hóa năm 2021 - 2022
- Đề thi thử vào lớp 10 môn Toán Trường TH - THCS Tây Hà Nội năm 2021 (lần 2)
- Đề thi thử vào lớp 10 môn Toán Trường THCS Tân Dân năm 2021 - 2022
- Đề thi thử vào lớp 10 môn Toán trường THCS Thị trấn Trạm Trôi, Hoài Đức năm 2020 - 2021
- Đề thi thử vào lớp 10 môn Toán trường THCS Nam Từ Liêm năm 2020 - 2021 (lần 1)
- Đề thi thử vào lớp 10 môn Toán phòng GD&ĐT huyện Thường Xuân năm 2021
- Đề thi thử vào lớp 10 môn Toán phòng GD&ĐT thành phố Vinh năm 2021 - 2022
- Đề thi thử vào lớp 10 môn Toán phòng GD&ĐT huyện Thanh Hà năm 2021 - 2022
- Đề thi thử vào lớp 10 môn Toán phòng GD&ĐT huyện Đông Anh năm 2021 - 2022
- Đề thi thử vào lớp 10 môn Toán Trường THCS Archimedes Academy năm 2020 - 2021 (lần 5)
- Đề thi thử vào lớp 10 môn Toán Trường THCS Thanh Xuân Nam năm 2020 - 2021
- Đề thi thử vào lớp 10 môn Toán Trường THCS Ngọc Lâm, Long Biên năm 2020 - 2021
- Đề thi thử vào lớp 10 môn Toán Phòng GD&ĐT huyện Ba Vì năm 2020 - 2021
- Đề thi thử vào lớp 10 môn Toán Trường THCS&THPT Nguyễn Tất Thành năm học 2021 - 2022
............................................
Ngoài Đề thi thử vào lớp 10 môn Toán Trường Đại học Sư Phạm Hà Nội năm học 2021 - 2022 (vòng 2). Mời các bạn học sinh còn có thể tham khảo các đề thi học kì 2 lớp 9 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề Thi vào lớp 10 năm 2021 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt
