Giải Chuyên đề Tin học 12 Chân trời sáng tạo bài 1: Các khái niệm cơ bản của đồ thị
Bài 1: Các khái niệm cơ bản của đồ thị
- Khởi động trang 49 Chuyên đề Tin 12 Chân trời
- Câu hỏi trang 50 Chuyên đề Tin 12 Chân trời
- Câu hỏi trang 51 Chuyên đề Tin 12 Chân trời
- Luyện tập trang 51 Chuyên đề Tin 12 Chân trời
- Thực hành 1 trang 51 Chuyên đề Tin 12 Chân trời
- Thực hành 2 trang 52 Chuyên đề Tin 12 Chân trời
- Vận dụng 1 trang 52 Chuyên đề Tin 12 Chân trời
- Vận dụng 2 trang 52 Chuyên đề Tin 12 Chân trời
VnDoc.com xin gửi tới bạn đọc bài viết Giải Chuyên đề Tin học 12 bài 1: Các khái niệm cơ bản của đồ thị để bạn đọc cùng tham khảo. Mời các bạn cùng tham khảo thêm tại mục Tin học 12 Chân trời sáng tạo.
Khởi động trang 49 Chuyên đề Tin 12 Chân trời
Một khách du lịch xuất phát từ sân bay của thành phố, muốn ghé thăm tất cả các địa điểm nổi tiếng A, B, C, D, E, F, mỗi địa điểm đúng một lân sau đỏ quay trở lại sân bay. Theo em, có tồn tại một hành trình như vậy không?
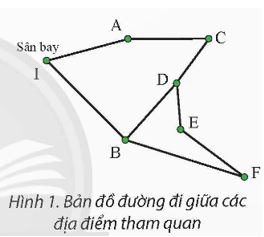
Lời giải:
Dựa trên bản đồ đường đi giữa các địa điểm tham quan trong hình ảnh, để có một hành trình ghé thăm mỗi địa điểm một lần và quay trở lại sân bay, mỗi địa điểm cần có một số chẵn các đường nối (để tạo thành một chu trình Euler). Tuy nhiên, trong hình ảnh:
Địa điểm B và D có số lượng đường nối lẻ.
Địa điểm F và Sân bay chỉ có một đường nối.
Do đó, dựa trên nguyên tắc của đường đi Euler và không có thông tin thêm về hướng di chuyển hay khoảng cách, một hành trình như vậy không tồn tại.
Câu hỏi trang 50 Chuyên đề Tin 12 Chân trời
Một mạng máy tính gồm có 7 máy tính được kết nối với một máy chủ thông qua một switch. Máy chủ được kết nối với mạng Internet thông qua modem. Ngoài ra, máy chủ còn được kết nối với 2 máy in. Em hãy:
a) Vẽ đồ thị biểu diễn mạng máy tính.
b) Cho biết đồ thị đó có bao nhiêu đỉnh, bao nhiêu cạnh?
Lời giải:
a) Vẽ đồ thị biểu diễn mạng máy tính
Chúng ta có một mạng máy tính gồm các thành phần sau:
1 máy chủ (Server)
7 máy tính (PC1, PC2, ..., PC7)
1 switch (Switch)
1 modem (Modem)
2 máy in (Printer1, Printer2)
Các kết nối là:
Máy chủ kết nối với switch.
7 máy tính kết nối với switch.
Máy chủ kết nối với modem (và modem kết nối với Internet).
Máy chủ kết nối với 2 máy in.
Dưới đây là đồ thị biểu diễn mạng máy tính này:

b) Cho biết đồ thị đó có bao nhiêu đỉnh, bao nhiêu cạnh?
Đỉnh (vertices): Các đỉnh đại diện cho các thiết bị trong mạng máy tính. Các đỉnh gồm:
1 modem
1 máy chủ
7 máy tính
1 switch
2 máy in
Tổng số đỉnh là: 1+1+7+1+2=121 + 1 + 7 + 1 + 2 = 121+1+7+1+2=12
Cạnh (edges): Các cạnh đại diện cho các kết nối giữa các thiết bị trong mạng. Các cạnh gồm:
1 cạnh giữa modem và máy chủ
1 cạnh giữa máy chủ và switch
7 cạnh giữa switch và 7 máy tính
2 cạnh giữa máy chủ và 2 máy in
Tổng số cạnh là: 1+1+7+2=111 + 1 + 7 + 2 = 111+1+7+2=11
Câu hỏi trang 51 Chuyên đề Tin 12 Chân trời
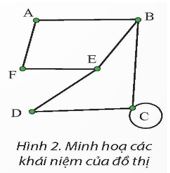
Em hãy cho biết trong các đồ thị ở Hình 5, đồ thị nào là đơn đồ thị, đồ thị vô hướng, đồ thị có hướng.

Lời giải:
Đơn đồ thị: Là đồ thị không có vòng lặp và không có nhiều cạnh giữa cùng một cặp đỉnh. “Hình 5b” biểu diễn một đơn đồ thị.
Đồ thị vô hướng: Là đồ thị mà các cạnh không có hướng. Các đồ thị trong “Hình 5a,” “Hình 5b,” và “Hình 5c” là đồ thị vô hướng vì các cạnh của chúng không có mũi tên chỉ hướng.
Đồ thị có hướng: Là đồ thị có các cạnh được biểu diễn bằng mũi tên chỉ hướng. Trong hình ảnh này, chỉ có “Hình 5e” phù hợp với mô tả này vì nó rõ ràng thể hiện mũi tên trên các cạnh của nó.
Luyện tập trang 51 Chuyên đề Tin 12 Chân trời
Cho đồ thị như ở Hình 6. Em hãy cho biết:
a) Tập các đỉnh và tập các cạnh của đồ thị.
b) Các đỉnh kề với đỉnh A, D.
c) Các cạnh kề với cạnh {C, E}, {D, F}.
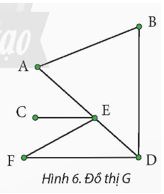
Lời giải:
a) Tập các đỉnh của đồ thị là: {A, B, C, D, E, F}. Tập các cạnh là: {{A, B}, {A, C}, {A, D}, {B, E}, {C, E}, {D, E}, {C, F}}.
b) Các đỉnh kề với đỉnh A là: B, C, D. Các đỉnh kề với đỉnh D là: A, E.
c) Các cạnh kề với cạnh {C, E} là: {{B, E}, {D, E}, {A, C}, {C, F}}. Đối với cạnh {D, F}, không có cạnh này trong đồ thị, nhưng nếu bạn muốn biết các cạnh kề với cạnh {D, E}, đó là: {{B, E}, {C, E}, {A, D}}.
Thực hành 1 trang 51 Chuyên đề Tin 12 Chân trời
Một nhóm 5 người A, B, C, D, E trong đó:
- A cùng tuổi với B.
- C cùng tuổi với D nhưng không cùng vớiAA.
- Riêng E không cùng tuổi với ai.
Hãy sử dụng đồ thị để biểu diễn quan hệ cùng tuổi của nhóm người này.
Lời giải:
a) Tập các đỉnh của đồ thị là: {A, B, C, D, E, F}. Tập các cạnh là: {{A, B}, {A, C}, {A, D}, {B, E}, {C, E}, {D, E}, {C, F}}.
b) Các đỉnh kề với đỉnh A là: B, C, D. Các đỉnh kề với đỉnh D là: A, E.
c) Các cạnh kề với cạnh {C, E} là: {{B, E}, {D, E}, {A, C}, {C, F}}. Đối với cạnh {D, F}, không có cạnh này trong đồ thị, nhưng nếu bạn muốn biết các cạnh kề với cạnh {D, E}, đó là: {{B, E}, {C, E}, {A, D}}.
Thực hành 2 trang 52 Chuyên đề Tin 12 Chân trời
Hình 7 là đồ thị cho biết sự tương tác giữa các loài động vật. Mỗi loài được biểu diễn bằng một đỉnh. Mỗi cạnh nối hai đỉnh thể hiện các loài này cạnh tranh với nhau (các loài có chung nguồn thức ăn).
Quan sát hình và cho biết những loài nào không cạnh tranh với nhau?
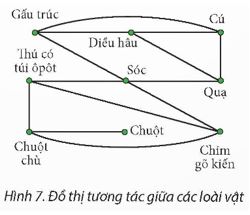
Lời giải:
Dựa vào mô tả của hình ảnh, các loài không cạnh tranh với nhau là:
Gấu trúc: Không cạnh tranh với Điểu hậu, Sóc, hoặc Quạ.
Chim gõ kiến: Không cạnh tranh với Điểu hậu, Sóc, hoặc Quạ.
Chim gõ kiến và Gấu trúc: Cũng không cạnh tranh với nhau.
Đây là một cách thú vị để hiển thị mối quan hệ phức tạp trong hệ sinh thái, nơi một số loài chia sẻ nguồn thức ăn dẫn đến cạnh tranh, trong khi những loài khác thì không.
Vận dụng 1 trang 52 Chuyên đề Tin 12 Chân trời
Trong một cuộc họp có hai người A và B chỉ nói được tiếng Anh, ba người C, D, E chỉ nói được tiếng Việt và một thông dịch viên I.
a) Để biểu diễn ai có thể giao tiếp trực tiếp được với nhau trong cuộc họp. Hãy vẽ đồ thị.
b) Cho biết có bao nhiêu người có thể giao tiếp trực tiếp được với B, E, I.
Lời giải:
a) Vẽ đồ thị biểu diễn ai có thể giao tiếp trực tiếp được với nhau trong cuộc họp
Người A và B chỉ nói được tiếng Anh.
Người C, D, E chỉ nói được tiếng Việt.
Thông dịch viên I có thể giao tiếp với tất cả mọi người.
Ta biểu diễn mỗi người như một đỉnh của đồ thị và vẽ cạnh giữa các đỉnh nếu hai người có thể giao tiếp trực tiếp với nhau.
Dưới đây là đồ thị biểu diễn:
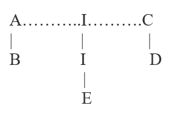
Trong đồ thị này:
A và B có thể giao tiếp trực tiếp với I.
C, D, và E có thể giao tiếp trực tiếp với I.
I có thể giao tiếp trực tiếp với tất cả mọi người.
b) Cho biết có bao nhiêu người có thể giao tiếp trực tiếp được với B, E, I
Người B có thể giao tiếp trực tiếp với:
Người A
Người I
=> Tổng cộng có 2 người (A, I).
Người E có thể giao tiếp trực tiếp với:
Người I
=> Tổng cộng có 1 người (I).
Người I có thể giao tiếp trực tiếp với:
Người A
Người B
Người C
Người D
Người E
=> Tổng cộng có 5 người (A, B, C, D, E).
Vận dụng 2 trang 52 Chuyên đề Tin 12 Chân trời
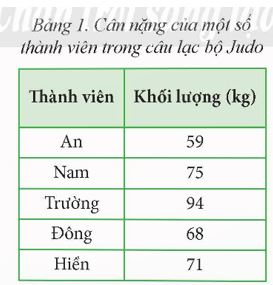
Bảng 1 cho biết cân nặng của một số thành viên trong một câu lạc bộ Judo. Hai người có thể thi đấu với nhau nếu cân nặng của họ hơn kém nhau không quá 10 kg. Theo em, những cặp nào có thể thi đầu được với nhau?
Lời giải:
Bảng 1 cho biết cân nặng của một số thành viên trong một câu lạc bộ Judo. Hai người có thể thi đấu với nhau nếu cân nặng của họ hơn kém nhau không quá 10 kg. Theo em, những cặp sau có thể thi đầu được với nhau”
An và Đông: Chênh lệch cân nặng là 9 kg.
Đông và Hiền: Chênh lệch cân nặng là 3 kg.
Những cặp này có sự chênh lệch cân nặng không quá 10 kg, do đó họ có thể thi đấu Judo với nhau theo tiêu chí đã cho.









