Giải Chuyên đề Tin học 12 Chân trời sáng tạo bài 2: Các phép toán duyệt cây nhị phân
Bài 2: Các phép toán duyệt cây nhị phân
VnDoc.com xin gửi tới bạn đọc bài viết Giải Chuyên đề Tin học 12 bài 2: Các phép toán duyệt cây nhị phân để bạn đọc cùng tham khảo. Mời các bạn cùng tham khảo thêm tại mục Tin học 12 Chân trời sáng tạo.
Khởi động trang 32 Chuyên đề Tin 12 Chân trời
Cho cây nhị phân như Hình 1. Hãy dùng mảng một chiều để biểu diễn các giá trị trong cây nhị phân.
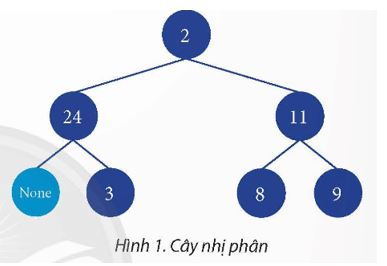
Lời giải:
Mảng một chiều để biểu diễn các giá trị trong cây nhị phân như sau:
[2, 24, 11, None, 3, 8, 9]
Câu hỏi trang 35 Chuyên đề Tin 12 Chân trời
Cho cây nhị phân như Hình 4.
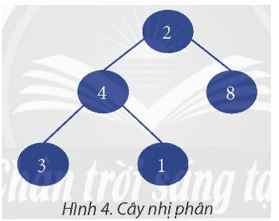
Kết quả thực hiện phép toán duyệt cây nhị phân như sau:
3 4 1 2 8
Phép toán duyệt cây nhị phân cho kết quả như bảng ở trên là phép toán nào?
Lời giải:
Phép toán duyệt cây nhị phân tạo ra kết quả ở bảng trên này là duyệt in-order. Ta sẽ thăm nút con bên trái, sau đó là nút hiện tại, và cuối cùng là nút con bên phải. Đối với cây tìm kiếm nhị phân, phép duyệt này sẽ cho kết quả là các giá trị được sắp xếp theo thứ tự tăng dần.
Câu hỏi trang 38 Chuyên đề Tin 12 Chân trời
Cho cây nhị phân như Hình 8. Biểu diễn các giá trị trong cây nhị phân bằng mảng một chiều theo:
a) Duyệt trước;
b) Duyệt giữa;
c) Duyệt sau.
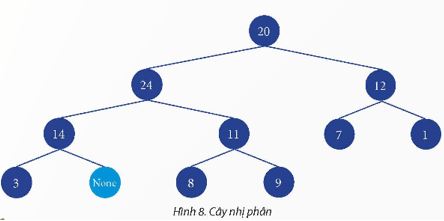
Lời giải:
Cách biểu diễn các giá trị của cây bằng mảng một chiều theo ba phép duyệt:
a) Duyệt trước (Pre-order): Thăm nút gốc trước, sau đó là cây con bên trái và cuối cùng là cây con bên phải. [20,24,14,None,None,None,None,None,None,None,None]
b) Duyệt giữa (In-order): Thăm cây con bên trái trước, sau đó là nút gốc và cuối cùng là cây con bên phải. None,None,None,None]
c) Duyệt sau (Post-order): Thăm cây con bên trái trước, sau đó là cây con bên phải và kết thúc ở nút gốc. [None]
Luyện tập trang 39 Chuyên đề Tin 12 Chân trời
Cho các thao tác: (1) Duyệt nút gốc; (2) Duyệt cây con trái; (3) Duyệt cây con phải. Sắp xếp thứ tự các thao tác tương ứng với các phép toán duyệt cây nhị phân:
a) Duyệt trước;
b) Duyệt giữa;
c) Duyệt sau.
Lời giải:
Cho các thao tác: (1) Duyệt nút gốc; (2) Duyệt cây con trái; (3) Duyệt cây con phải. Sắp xếp thứ tự các thao tác tương ứng với các phép toán duyệt cây nhị phân:
a) Duyệt trước:
Thao tác: Duyệt nút gốc -> Duyệt cây con trái -> Duyệt cây con phải
Thứ tự: (1) -> (2) -> (3)
b) Duyệt giữa:
Thao tác: Duyệt cây con trái -> Duyệt nút gốc -> Duyệt cây con phải
Thứ tự: (2) -> (1) -> (3)
c) Duyệt sau:
Thao tác: Duyệt cây con trái -> Duyệt cây con phải -> Duyệt nút gốc
Thứ tự: (2) -> (3) -> (1)
Thực hành trang 39 Chuyên đề Tin 12 Chân trời
Cho mảng số nguyên dương A = [5, 8, 7, 4, 9, 2).
a) Xây dựng cây nhị phân với mảng số nguyên dương trên.
b) Sử dụng phép toán duyệt trước, duyệt giữa, duyệt sau để xuất thứ tự các giá trị trên
cây nhị phân được xây dựng ở câu a).
Lời giải:
Cho mảng số nguyên dương A = [5, 8, 7, 4, 9, 2).
a) Xây dựng cây nhị phân với mảng số nguyên dương: A = [5, 8, 7, 4, 9, 2).
- Phần tử đầu tiên 5 là gốc.
- lớn hơn 5, đặt vào cây con phải của 5.
- 7 nhỏ hơn 8, đặt vào cây con trái của 8.
- 4 nhỏ hơn 5, đặt vào cây con trái của 5.
- 9 lớn hơn 8, đặt vào cây con phải của 8.
- 2 nhỏ hơn 4, đặt vào cây con trái của 4.
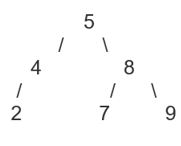
b) Sử dụng phép toán duyệt trước, duyệt giữa, duyệt sau để xuất thứ tự các giá trị trên cây nhị phân được xây dựng ở câu a).
- Duyệt trước (Pre-order traversal):
Duyệt nút gốc -> Duyệt cây con trái -> Duyệt cây con phải
Thứ tự: 5 -> 4 -> 2 -> 8 -> 7 -> 9
- Duyệt giữa (In-order traversal):
Duyệt cây con trái -> Duyệt nút gốc -> Duyệt cây con phải
Thứ tự: 2 -> 4 -> 5 -> 7 -> 8 -> 9
- Duyệt sau (Post-order traversal):
Duyệt cây con trái -> Duyệt cây con phải -> Duyệt nút gốc
Thứ tự: 2 -> 4 -> 7 -> 9 -> 8 -> 5
Vận dụng trang 39 Chuyên đề Tin 12 Chân trời
Cho mảng các số nguyên dương A = [9, 6, 5, 17, 10, 3, 8, 12].
a) Xây dựng cây nhị phân với mảng số nguyên dương trên.
b) Viết chương trình có sử dụng phép toán duyệt trước, duyệt giữa, duyệt sau để:
- Kiểm tra giá trị 10 có trong cây hay không?
- Kiểm tra giá trị 7 có trong cây hay không?
Lời giải:
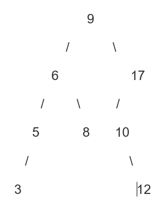
a) Xây dựng cây nhị phân với mảng số nguyên dương A = [9, 6, 5, 17, 10, 3, 8, 12]
Chúng ta sẽ xây dựng cây nhị phân tìm kiếm (BST) từ mảng A:
Phần tử đầu tiên 9 là gốc.
6 nhỏ hơn 9, đặt vào cây con trái của 9.
5 nhỏ hơn 6, đặt vào cây con trái của 6.
17 lớn hơn 9, đặt vào cây con phải của 9.
10 nhỏ hơn 17, đặt vào cây con trái của 17.
3 nhỏ hơn 5, đặt vào cây con trái của 5.
8 lớn hơn 6, đặt vào cây con phải của 6.
12 lớn hơn 10, đặt vào cây con phải của 10.
b) Viết chương trình kiểm tra giá trị trong cây và thực hiện duyệt cây:
Code:
class Node:
def __init__(self, key):
self.left = None
self.right = None
self.val = key
def insert(root, key):
if root is None:
return Node(key)
else:
if root.val < key:
root.right = insert(root.right, key)
else:
root.left = insert(root.left, key)
return root
def search(root, key):
if root is None or root.val == key:
return root
if root.val < key:
return search(root.right, key)
return search(root.left, key)
def preOrder(root):
if root:
print(root.val, end=" ")
preOrder(root.left)
preOrder(root.right)
def inOrder(root):
if root:
inOrder(root.left)
print(root.val, end=" ")
inOrder(root.right)
def postOrder(root):
if root:
postOrder(root.left)
postOrder(root.right)
print(root.val, end=" ")
# Mảng số nguyên dương
A = [9, 6, 5, 17, 10, 3, 8, 12]
# Xây dựng cây nhị phân
root = None
for key in A:
root = insert(root, key
# Duyệt cây
print("Duyệt trước:")
preOrder(root)
print("\nDuyệt giữa:")
inOrder(root)
print("\nDuyệt sau:")
postOrder(root)
print()
# Kiểm tra giá trị
def check_value(root, value):
if search(root, value):
print(f"Giá trị {value} có trong cây.")
else:
print(f"Giá trị {value} không có trong cây.")
# Kiểm tra giá trị 10 và 7
check_value(root, 10)
check_value(root, 7)









