Giải Chuyên đề Tin học 12 Chân trời sáng tạo bài 2: Ngăn xếp
Bài 2: Ngăn xếp
- Khởi động trang 10 Chuyên đề Tin 12 Chân trời
- Câu hỏi trang 11 Chuyên đề Tin 12 Chân trời
- Câu hỏi 1 trang 12 Chuyên đề Tin 12 Chân trời
- Câu hỏi 2 trang 12 Chuyên đề Tin 12 Chân trời
- Luyện tập 1 trang 13 Chuyên đề Tin 12 Chân trời
- Luyện tập 2 trang 13 Chuyên đề Tin 12 Chân trời
- Vận dụng 1 trang 13 Chuyên đề Tin 12 Chân trời
- Vận dụng 2 trang 13 Chuyên đề Tin 12 Chân trời
- Vận dụng 3 trang 13 Chuyên đề Tin 12 Chân trời
Giải Chuyên đề Tin học 12 Ngăn xếp là tài liệu hữu ích được VnDoc.com tổng hợp và gửi tới bạn đọc cùng theo dõi để có thêm tài liệu học tập môn Tin học 12 Chân trời sáng tạo.
Khởi động trang 10 Chuyên đề Tin 12 Chân trời
Quan sát Hình 1 và cho biết cách thêm đĩa mới vào và lấy ra một đĩa từ chồng đĩa.
Lời giải:
Quan sát Hình 1, ta thấy cách thêm đĩa mới vào và lấy ra một đĩa từ chồng đĩa như sau:
- Thêm đĩa mới vào: Đặt đĩa mới lên trên đĩa lớn nhất hiện có trên cùng của cọc.
- Lấy ra đĩa: Lấy đĩa nhỏ nhất ra từ đỉnh của bất kỳ cọc nào nhưng không làm xáo trộn thứ tự của các đĩa khác.
Câu hỏi trang 11 Chuyên đề Tin 12 Chân trời
Hình 4 biểu diễn một ngăn xếp. Cho biết:
a) Phần tử nào ở đỉnh của ngăn xếp.
b) Sau khi lấy ra một phần tử, thì ngăn xếp gồm các phần tử nào.
c) Sau khi thêm phần tử "X" vào, thì phần tử nào ở đỉnh của ngăn xếp.
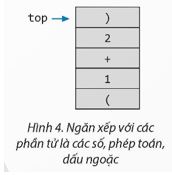
Lời giải:
Hình 4 biểu diễn một ngăn xếp, ta có:
a) Phần tử ở đỉnh của ngăn xếp là dấu ngoặc đơn phải “)”.
b) Sau khi lấy ra một phần tử (dấu ngoặc đơn phải), ngăn xếp còn lại gồm các phần tử: “2”, “+”, và “1”.
c) Sau khi thêm phần tử “X” vào, phần tử “X” sẽ ở đỉnh của ngăn xếp.
Câu hỏi 1 trang 12 Chuyên đề Tin 12 Chân trời
Để biểu diễn ngăn xếp bằng mảng một chiều, em cần sử dụng những thông tin gì?
Lời giải:
Để biểu diễn ngăn xếp bằng mảng một chiều, em cần sử dụng những thông tin sau:
- Cần mảng một chiều để lưu trữ các phần tử của ngăn xếp.
- Kích thước của mảng 1 chiều: chính là kích thước của các phần tử trong ngăn xếp.
- Chỉ số Top: Trả về giá trị của của phần tử ở đỉnh của ngăn xếp bằng cách trả về giá trị của phần tử cuối mảng.
Câu hỏi 2 trang 12 Chuyên đề Tin 12 Chân trời
Vì sao có thể dùng danh sách (kiểu list của Python) để biểu diễn ngăn xếp?
Lời giải:
Có thể dùng danh sách (kiểu list của Python) để biểu diễn ngăn xếp vì: danh sách cung cấp các phương thức append(), pop() và tính năng phù hợp để thực hiện các thao tác cần thiết của một ngăn xếp một cách dễ dàng và hiệu quả.
Luyện tập 1 trang 13 Chuyên đề Tin 12 Chân trời
Trong Python, khi sử dụng kiểu list để biểu diễn ngăn xếp. Hãy cho biết:
a) Chỉ số của phần tử đỉnh.
- Phần tử đỉnh là phần tử cuối cùng trong danh sách.
- Trong Python, chỉ số của phần tử cuối cùng trong danh sách là -1.
b) Chỉ số của phần tử đáy.
- Phần tử đáy là phần tử đầu tiên trong danh sách.
- Trong Python, chỉ số của phần tử đầu tiên trong danh sách là 0.
Lời giải:
Trong Python, khi sử dụng kiểu list để biểu diễn ngăn xếp.
a) Chỉ số của phần tử đỉnh.
b) Chỉ số của phần tử đáy.
Luyện tập 2 trang 13 Chuyên đề Tin 12 Chân trời
Hãy vẽ lại Hình 5, cập nhật giá trị top khi thực hiện tuần tự các thao tác sau đây: push(0), pop(), pop(), push(100).
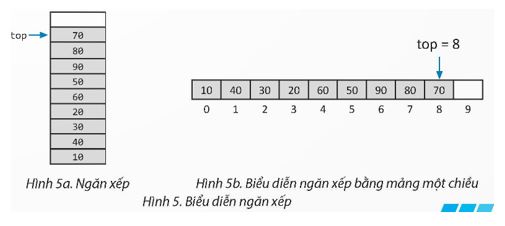
Lời giải:
Vẽ lại Hình 5, cập nhật giá trị top khi thực hiện tuần tự các thao tác sau đây: push(0), pop(), pop(), push(100).
- push(0): Thêm giá trị ‘0’ vào vị trí top hiện tại (index 8), sau đó cập nhật giá trị top thành 8.
- pop(): Loại bỏ giá trị ‘0’ khỏi vị trí top (index 8), sau đó cập nhật giá trị top thành 7.
- pop(): Loại bỏ giá trị ‘80’ khỏi vị trí top (index 7), sau đó cập nhật giá trị top thành 6.
- push(100): Thêm giá trị ‘100’ vào vị trí top hiện tại (index 6), sau đó cập nhật giá trị top thành 6.
Kết quả: Đây là cách cập nhật biểu diễn ngăn xếp sau các thao tác chỉnh sửa dữ liệu theo nguyên tắc LIFO (Last In First Out).
- Hình 5a có ‘70’ ở đỉnh ngăn xếp.
- Hình 5b sẽ có ‘100’ ở index 6 các index từ 0 đến 5 không có giá trị, index 7 và 8 trống, và index 9 không thay đổi.
Vận dụng 1 trang 13 Chuyên đề Tin 12 Chân trời
Để tính giá trị một biểu thức số học bằng máy tính, một số nhà khoa học đã sử dụng cách biểu diễn dạng tiền tố (hay còn gọi là kí pháp Ba lan). Ví dụ, biểu thức số học (2-7/3)*(4-1) sẽ được chuyển sang dạng tiền tố có dạng *-2/73-41 (toán tử đặt trước toán hạng) trước khi tính giá trị. Sử dụng các hàm initStack(), push() để tạo ngăn xếp có các phần tử như sau:

Lời giải:
Để tính giá trị một biểu thức số học bằng máy tính, một số nhà khoa học đã sử dụng cách biểu diễn dạng tiền tố (hay còn gọi là kí pháp Ba lan). Ví dụ, biểu thức số học (2-7/3)*(4-1) sẽ được chuyển sang dạng tiền tố có dạng *-2/73-41 (toán tử đặt trước toán hạng) trước khi tính giá trị. Sử dụng các hàm initStack(), push() để tạo ngăn xếp có các phần tử như sau:
Bước 1: Khởi tạo ngăn xếp và đẩy các phần tử của biểu thức gốc vào ngăn xếp.
Bước 2: Sử dụng ngăn xếp để chuyển đổi biểu thức từ dạng trung tố sang tiền tố bằng cách sử dụng các thao tác push và pop.
Code:
class Stack:
def __init__(self):
self.stack = []
def push(self, item):
self.stack.append(item)
def pop(self):
if not self.is_empty():
return self.stack.pop()
return None
def peek(self):
if not self.is_empty():
return self.stack[-1]
return None
def is_empty(self):
return len(self.stack) == 0
def initStack():
s = Stack()
elements = ["(", "2", "-", "7", "/", "3", ")", "*", "(", "4", "-", "1", ")"]
for element in elements:
s.push(element)
return s
def infix_to_prefix(stack):
operators = set(['+', '-', '*', '/', '(', ')'])
precedence = {'+': 1, '-': 1, '*': 2, '/': 2}
output = []
operator_stack = Stack()
while not stack.is_empty():
token = stack.pop()
if token.isdigit():
output.append(token)
elif token == '(':
while not operator_stack.is_empty() and operator_stack.peek() != ')':
output.append(operator_stack.pop())
operator_stack.pop() # pop ')'
elif token == ')':
operator_stack.push(token)
else:
while (not operator_stack.is_empty() and
precedence.get(token, 0) <= precedence.get(operator_stack.peek(), 0)):
output.append(operator_stack.pop())
operator_stack.push(token)
while not operator_stack.is_empty():
output.append(operator_stack.pop())
return output[::-1] # Đảo ngược danh sách để có dạng tiền tố
# Khởi tạo ngăn xếp
stack = initStack()
# Chuyển biểu thức từ trung tố sang tiền tố
result = infix_to_prefix(stack)
# In kết quả
print(" ".join(result)) # Output: * - 2 / 7 3 - 4 1
Giải thích:
- Lớp Stack: Định nghĩa các phương thức cơ bản cho ngăn xếp (push, pop, peek, is_empty).
- Hàm initStack(): Khởi tạo ngăn xếp và đẩy các phần tử của biểu thức vào ngăn xếp.
- Hàm infix_to_prefix(): Chuyển đổi biểu thức từ dạng trung tố sang tiền tố bằng cách sử dụng ngăn xếp. Hàm này đọc từng phần tử từ ngăn xếp, xử lý các toán tử và toán hạng theo nguyên tắc của biểu thức tiền tố, và đẩy kết quả cuối cùng vào danh sách output.
- Kết quả: In ra biểu thức tiền tố.
Vận dụng 2 trang 13 Chuyên đề Tin 12 Chân trời
Theo em dùng danh sách liên kết để biểu diễn ngăn xếp được hay không?
Lời giải:
Theo em có thể dùng danh sách liên kết để biểu diễn ngăn xếp được. Vì hực tế, danh sách liên kết cung cấp một số lợi thế nhất định so với mảng, đặc biệt khi bạn cần thực hiện các thao tác thêm (push) và xóa (pop) phần tử ở đầu ngăn xếp một cách hiệu quả. Nó còn có 1 số ưu điểm sau:
- Kích thước linh hoạt: Danh sách liên kết không có giới hạn về kích thước cố định như mảng. Bạn có thể thêm hoặc xóa phần tử mà không cần lo lắng về việc tràn ngăn xếp.
- Hiệu suất cao cho các thao tác thêm/xóa: Thao tác thêm hoặc xóa một phần tử ở đầu danh sách liên kết có độ phức tạp thời gian là O(1)O(1)O(1), trong khi đối với mảng, thao tác thêm/xóa phần tử ở đầu có thể có độ phức tạp thời gian là O(n)O(n)O(n).
Vận dụng 3 trang 13 Chuyên đề Tin 12 Chân trời
Tạo tệp stack.py chứa các hàm push(), pop(), top(), is EmptyStack() của ngăn xếp. Sau đó:
- Tạo ngăn xếp rỗng.
- Thực hiện các hàm push() với giá trị thích hợp để ngăn xếp có kết quả như Hình 6a.
- Thực hiện các hàm push), pop() với các giá trị thích hợp để ngăn xếp có kết quả như Hình 6b.
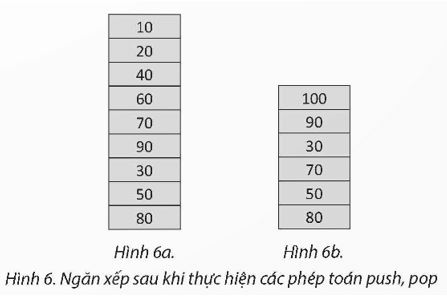
Lời giải:
Tạo tệp stack.py chứa các hàm push(), pop(), top(), is EmptyStack() của ngăn xếp. Sau đó:
- Tạo ngăn xếp rỗng.
- Thực hiện các hàm push() với giá trị thích hợp để ngăn xếp có kết quả như Hình 6a.
- Thực hiện các hàm push), pop() với các giá trị thích hợp để ngăn xếp có kết quả như Hình 6b.
Code như sau
class Stack:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def push(self, item):
self.items.append(item)
def pop(self):
if not self.isEmpty():
return self.items.pop()
def top(self):
if not self.isEmpty():
return self.items[-1]
# Tạo ngăn xếp rỗng
stack = Stack()
# Thực hiện các hàm push() để ngăn xếp có kết quả như Hình 6a
for value in [70, 60, 40, 20, 10]:
stack.push(value)
# Thực hiện các hàm pop() và push() để ngăn xếp có kết quả như Hình 6b
for _ in range(3): # Pop 3 lần để loại bỏ 10, 20, 40
stack.pop()
for value in [50, 70, 30, 90, 100]: # Push các giá trị mới
stack.push(value)









