Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

Đóng

Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm

Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169

VnDoc.com

Đề thi học kì 1 Toán 8 Chân trời sáng tạo (Đề 1)

Đề thi HK1 Toán 8

Bài trước

Tải về

Bài sau

Lớp: Lớp 8

Môn: Toán

Bộ sách: Chân trời sáng tạo

Loại File: PDF

Phân loại: Tài liệu Tính phí

Mời các bạn học cùng thử sức với Đề thi học kì 1 môn Toán lớp 8 - có đáp án theo chương trình sách Chân trời sáng tạo nha!

Đề thi học kì 1 Toán lớp 8 Chân trời sáng tạo

PHÒNG GD&ĐT …….

TRƯỜNG THCS……

CỘNG HÒA XÃ HỘI CHỦ NGHĨA VIỆT NAM

Độc lập - Tự do - Hạnh phúc

Thời gian: 90 phút (không kể thời gian phát đề)

I. Trắc nghiệm (3 điểm)

(Hãy chọn các đáp án đúng nhất trong các đáp án sau)

Câu 1. Trong các biểu thức sau, biểu thức nào là đơn thức?

$\sqrt {2 + {a^2}b}$ $\sqrt {2 + {a^2}b}$
$- \sqrt {11} {a^4}{b^5}$ $- \sqrt {11} {a^4}{b^5}$
$\frac{{{a^3} + b}}{{3b}}$ $\frac{{{a^3} + b}}{{3b}}$
${a^2} - 2ab + {b^2}$ ${a^2} - 2ab + {b^2}$

Câu 2. Thu gọn đơn thức $\frac{{3{{\left( { - 4{x^2}y} \right)}^2}.{y^2}}}{{16}}$ $\frac{{3{{\left( { - 4{x^2}y} \right)}^2}.{y^2}}}{{16}}$ thu được kết quả là:

$3{x^4}{y^4}$ $3{x^4}{y^4}$
$- 3{x^4}{y^4}$ $- 3{x^4}{y^4}$
$\frac{{3{x^2}{y^4}}}{4}$ $\frac{{3{x^2}{y^4}}}{4}$
$- \frac{{3{x^2}{y^4}}}{4}$ $- \frac{{3{x^2}{y^4}}}{4}$

Câu 3. Rút gọn đa thức: $A = 5{x^2}{y^2} - 3{x^2}{y^3} - 7{x^2}{y^2} + 3{x^2}{y^3} + 4$ $A = 5{x^2}{y^2} - 3{x^2}{y^3} - 7{x^2}{y^2} + 3{x^2}{y^3} + 4$ ta được kết quả:

$A = 6{x^2}{y^3} - 12{x^2}{y^2} - 4$ $A = 6{x^2}{y^3} - 12{x^2}{y^2} - 4$
$A = 12{x^2}{y^2}$ $A = 12{x^2}{y^2}$
$A = - 2{x^2}{y^2} + 4$ $A = - 2{x^2}{y^2} + 4$
$A = - 6{x^2}{y^3} - 2{x^2}{y^2}$ $A = - 6{x^2}{y^3} - 2{x^2}{y^2}$

Câu 4. Khai triển hằng đẳng thức ${\left( {x - 2} \right)^2}$ ${\left( {x - 2} \right)^2}$ ta được kết quả:

${x^2} + 2x + 4$ ${x^2} + 2x + 4$
${x^2} - 4x + 4$ ${x^2} - 4x + 4$
${x^2} + 4x + 2$ ${x^2} + 4x + 2$
${x^2} + 4x + 4$ ${x^2} + 4x + 4$

Câu 5. Trong các biểu thức cho dưới đây, biểu thức nào không phải là phân thức?

$2m + \sqrt 5 {m^2}n$ $2m + \sqrt 5 {m^2}n$
$\frac{{5ab}}{{\sqrt 3 c}}$ $\frac{{5ab}}{{\sqrt 3 c}}$
$\frac{{\sqrt {zt} }}{9}$ $\frac{{\sqrt {zt} }}{9}$
$\frac{{2x + y}}{{x - 3y}}$ $\frac{{2x + y}}{{x - 3y}}$

Câu 6. Chọn đáp án đúng? Với điều kiện $B \ne 0$ $B \ne 0$ ta có:

$\frac{A}{B} = \frac{{A.T}}{{B.T}},\left( {T \ne 0} \right)$ $\frac{A}{B} = \frac{{A.T}}{{B.T}},\left( {T \ne 0} \right)$
$\frac{A}{B} = \frac{{A:T}}{{B:T}}$ $\frac{A}{B} = \frac{{A:T}}{{B:T}}$ (T là nhân tử chung của A và B)
$\frac{A}{B} = \frac{{A.T}}{{B:T}},\left( {T \ne 0} \right)$ $\frac{A}{B} = \frac{{A.T}}{{B:T}},\left( {T \ne 0} \right)$
$\frac{A}{B} = \frac{{A.T}}{{B.T}}$ $\frac{A}{B} = \frac{{A.T}}{{B.T}}$ (T là nhân tử chung của A và B)

Câu 7. Tìm phân thức bằng với phân thức $\frac{{t - 1}}{{{t^3} - 1}}$ $\frac{{t - 1}}{{{t^3} - 1}}$ trong các phân thức cho dưới đây?

$\frac{1}{{{t^2} - 1}}$ $\frac{1}{{{t^2} - 1}}$
$\frac{{t - 1}}{{t + 1}}$ $\frac{{t - 1}}{{t + 1}}$
$\frac{1}{{{t^2} + t + 1}}$ $\frac{1}{{{t^2} + t + 1}}$
$\frac{t}{{t + 1}}$ $\frac{t}{{t + 1}}$

Câu 8. Hình chóp tứ giác đều có mặt đáy là hình gì?

Hình thang vuông
Hình thang
Tứ giác
Hình vuông

Câu 9. Chọn phát biểu đúng?

Hình chóp tam giác đều có:

Các mặt bên là tam giác đều.
Tất cả các cạnh bằng nhau.
Các cạnh bên bằng nhau và đáy là hình tam giác đều.
Các mặt bên là tam giác vuông.

Câu 10. Cho hình chóp tứ giác đều có trung đoạn bằng $4cm$, cạnh đáy bằng $6cm$. Tính diện tích xung quanh hình chóp tứ giác đều đó?

$24cm^2$
$48cm^2$
$144cm^2$
$96cm^2$

Câu 11. Cho hình thang cân $ABCD, (AB // CD)$ có $\widehat A = {120^0}$ $\widehat A = {120^0}$. Hỏi số đo góc $\widehat C$ $\widehat C$ bằng bao nhiêu?

$\widehat C = {60^0}$ $\widehat C = {60^0}$
$\widehat C = {120^0}$ $\widehat C = {120^0}$
$\widehat C = {90^0}$ $\widehat C = {90^0}$
$\widehat C = {100^0}$ $\widehat C = {100^0}$

Câu 12. Chọn phương án phù hợp để thống kê dữ liệu về phương tiện đến trường của học sinh (xe bus, xe máy, xe đạp điện, …)?

Quan sát.
Phỏng vấn, lập phiếu thăm dò.
Tìm kiếm trên mạng xã hội.
Làm thực nghiệm tại trường.

II. Tự luận (7 điểm)

Câu 1. Thực hiện các phép tính sau:

a) $- xy\left( {7{x^2} - 5xy} \right)$ $- xy\left( {7{x^2} - 5xy} \right)$

b) $\left( {3x + 7y} \right)\left( {3x - 7y} \right)$ $\left( {3x + 7y} \right)\left( {3x - 7y} \right)$

c) $\left( {10{x^2}y + 8x{y^2} - 5xy} \right):\left( { - xy} \right)$ $\left( {10{x^2}y + 8x{y^2} - 5xy} \right):\left( { - xy} \right)$

Câu 2. Phân tích đa thức sau thành nhân tử:

${x^2} - 5xy - 4x + 20y$ ${x^2} - 5xy - 4x + 20y$

Câu 3. Rút gọn các phép tính:

a) ${\left( {2x - 1} \right)^2} + \left( {4x + 2} \right)\left( {1 - x} \right)$ ${\left( {2x - 1} \right)^2} + \left( {4x + 2} \right)\left( {1 - x} \right)$

b) $\frac{1}{{x + 2}} - \frac{x}{{{x^2} - 4}} + \frac{2}{{x - 2}}$ $\frac{1}{{x + 2}} - \frac{x}{{{x^2} - 4}} + \frac{2}{{x - 2}}$

Câu 4. Cho tam giác $ABC$ cân tại $A$. Gọi $M, N$ lần lượt là trung điểm các cạnh $BC$ và $AB$.

a) Chứng minh rằng tứ giác $ANMC$ là hình thang.

b) Gọi $E$ là điểm đối xứng của $M$ qua $N$. Chứng minh rằng $AMBE$ là hình chữ nhật.

Câu 5. Tính thể tích mẫu vật như hình vẽ:

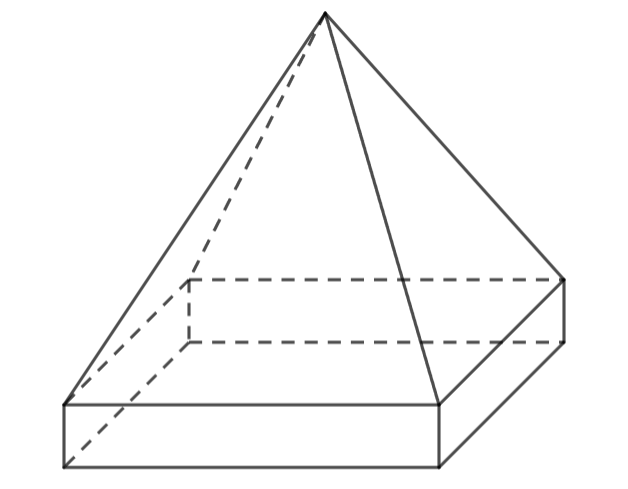
Đề thi học kì 1 Toán 8 Chân trời sáng tạo (Đề 1)

Biết phần trên của mẫu vật là hình chóp tứ giác đều có cạnh đáy và chiều cao lần lượt là $40cm$ và $30cm$, phần dưới của mẫu vật là hình hộp chữ nhật có đáy là hình vuông cạnh $40cm$ và chiều cao $10cm$.

Câu 6. Hai cột điện $A$ và $B$ được đặt cách nhau 24m và cách đều cột đèn $E$. Nhà Hoa cách cột đèn $E$ một khoảng 9m theo hướng vuông góc với đường nối hai cột điện $A$ và $B$ (như hình vẽ).

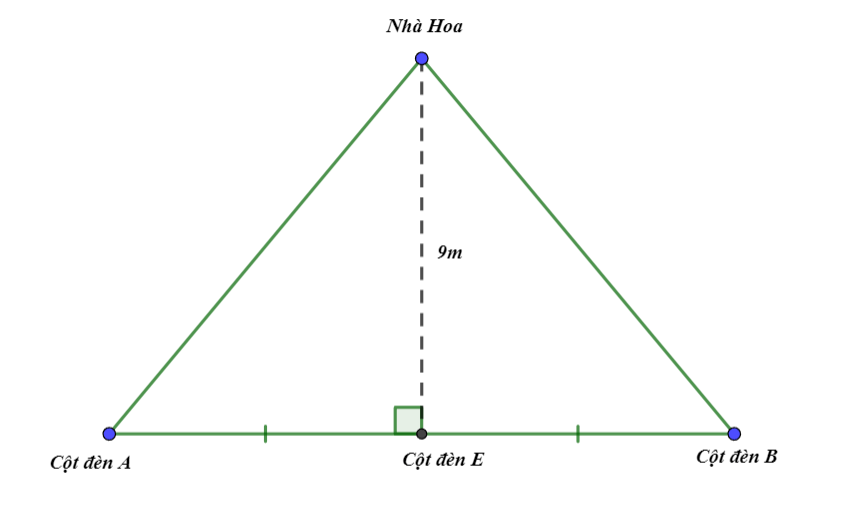
Đề thi học kì 1 Toán 8 Chân trời sáng tạo (Đề 1)

Tính khoảng cách từ nhà Hoa đến mỗi cột đèn.

Câu 7. Cho biểu đồ hình tròn biểu diễn tỉ lệ phân bố chi phí phát sinh trong việc xuất bản một cuốn sách. Nghiên cứu biểu đồ hình tròn và trả lời câu hỏi:

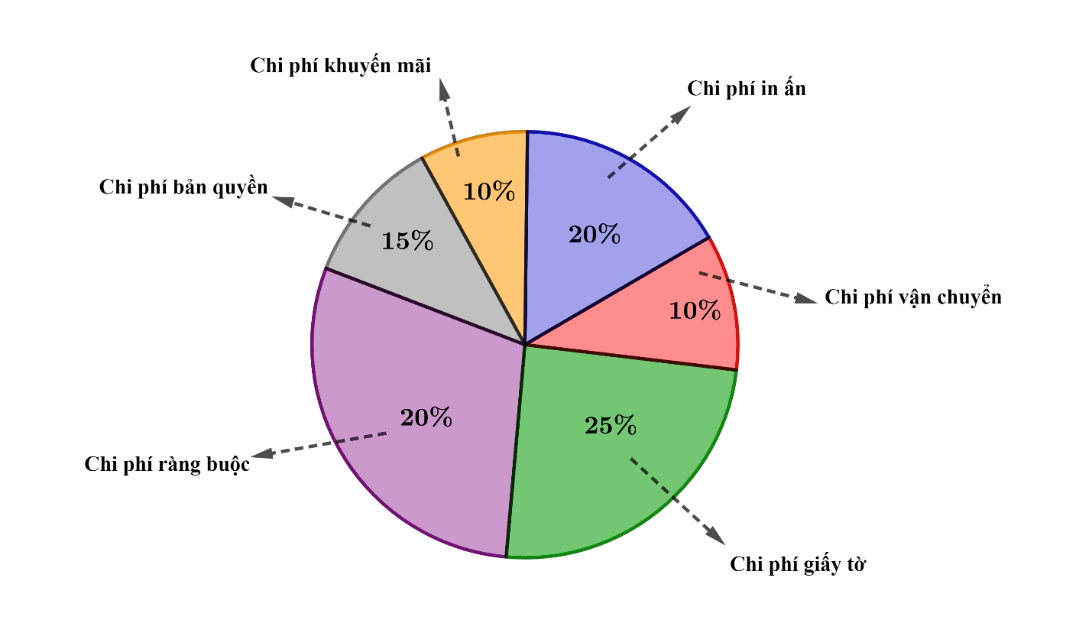
Đề thi học kì 1 Toán 8 Chân trời sáng tạo (Đề 1)

a) Lập bảng thống kê tương ứng với biểu đồ trên.

b) Đối với một ấn bản gồm $12500$ bản, số tiền bản quyền mà nhà xuất bản phải trả là $81.562.500$ đồng. Nếu nhà xuất bản mong muốn lợi nhuận là $5%$ thì giá bán một cuốn sách bằng bao nhiêu?

(Đáp án đề thi có trong file PDF, mời bạn đọc tải đề tham khảo)

Tải về

Chọn file muốn tải về: