VnDoc.com

Bài tập Vật lý 9 Bài 6: Bài tập vận dụng định luật Ôm

Bài tập vận dụng định luật Ôm Vật lý 9 - Có đáp án

Bài trước

Tải về

Bài sau

Bài tập vận dụng định luật Ôm - Có đáp án

I. Nhắc lại kiến thức Định luật Ôm
II. Bài tập vận dụng Định luật Ôm

Mời quý thầy cô cùng các em học sinh tham khảo tài liệu Bài tập Vật lý 9 Bài 6: Bài tập vận dụng định luật Ôm do VnDoc.com biên soạn và đăng tải. Tài liệu Bài tập vận dụng định luật Ôm này với các bài tập vận dụng được xây dựng trên lý thuyết trọng tâm bài học, hỗ trợ quá trình củng cố bài học và ôn luyện nâng cao khả năng làm bài tập môn Vật lý 9. Mời thầy cô cùng các bạn học sinh tham khảo.

Bản quyền thuộc về VnDoc.
Nghiêm cấm mọi hình thức sao chép nhằm mục đích thương mại.

I. Nhắc lại kiến thức Định luật Ôm

- Định luật Ôm: Cường độ dòng điện chạy qua dây dẫn tỉ lệ thuận với hiệu điện thế đặt vào hai đầu dây và tỉ lệ nghịch với điện trở của dây. _{$I = \frac{U}{R}$}

- Đoạn mạch song song gồm n điện trở _{$R_{1}, R_{2}, R_{3}, . . . ., R_{n}$} mắc song song, ta có các tính chất sau:

+ Cường độ dòng điện chạy qua đoạn mạch bằng tổng cường độ dòng điện chạy qua từng điện trở _{$I_{A B} = I_{1} + I_{2} + . . . . + I_{n}$}

+ Hiệu điện thế giữa hai đoạn mạch gồm các điện trở mắc song song bằng hiệu điện thế giữa hai đầu mỗi điện trở thành phần ${{U}_{AB}}={{U}_{1}}={{U}_{2}}=....={{U}_{n}}$ $U_{A B} = U_{1} = U_{2} = . . . . = U_{n}$

- Điện trở tương đương của đoạn mạch song song bằng tổng các điện trở thành phần: $\frac{1}{{{R}_{td}}}=\frac{1}{{{R}_{1}}}+\frac{1}{{{R}_{2}}}+...+\frac{1}{{{R}_{n}}}$ $\frac{1}{R_{t d}} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + . . . + \frac{1}{R_{n}}$

- Đoạn mạch nối tiếp gồm n điện trở _{$R_{1}, R_{2}, R_{3}, . . . ., R_{n}$} mắc nối tiếp, ta có các tính chất sau:

+ Cường độ dòng điện chạy qua đoạn mạch bằng cường độ dòng điện chạy qua từng điện trở ${{I}_{AB}}={{I}_{1}}={{I}_{2}}=....={{I}_{n}}$ $I_{A B} = I_{1} = I_{2} = . . . . = I_{n}$

+ Hiệu điện thế giữa hai đoạn mạch gồm các điện trở mắc nối tiếp bằng tổng hiệu điện thế giữa hai đầu mỗi điện trở thành phần _{$U_{A B} = U_{1} + U_{2} + . . . . + U_{n}$}

+ Trong đoạn mạch gồm hai điện trở mắc nối tiếp, hiệu điện thế giữa hai đầu mỗi điện trở tỉ lệ thuận với điện trở đó: _{$\frac{U_{1}}{U_{2}} = \frac{R_{1}}{R_{2}}$}

+ Điện trở tương đương của đoạn mạch nối tiếp bằng tổng các điện trở thành phần: ${{R}_{td}}={{R}_{1}}+{{R}_{2}}+...+{{R}_{n}}$ $R_{t d} = R_{1} + R_{2} + . . . + R_{n}$

II. Bài tập vận dụng Định luật Ôm

Bài tập 1: Cho đoạn mạch gồm 3 điện trở được mắc như sau: _{$R_{1} n t (R_{2} / / R_{3}); R_{1} = 20 Ω, R_{2} = R_{3} = 30 Ω$} được đặt vào hai đầu hiệu điện thế _{$U = 25 V$}

a. Tính cường độ dòng điện hai đầu đoạn mạch

b. Tính hiệu điện thế hai đầu _{$R_{1}$}

c. Tính cường độ dòng điện chạy qua _{$R_{3}$}

Hướng dẫn giải

Bài toán được mô tả bằng hình vẽ sau:

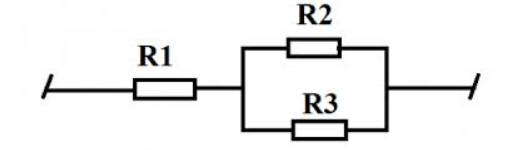
Bài tập Vật lý 9 Bài 6: Bài tập vận dụng định luật Ôm

${{R}_{23}}=\frac{{{R}_{2}}.{{R}_{3}}}{{{R}_{2}}+{{R}_{3}}}=\frac{30.30}{30+30}=15\Omega$ $R_{23} = \frac{R_{2} . R_{3}}{R_{2} + R_{3}} = \frac{30.30}{30 + 30} = 15 Ω$

$\begin{align} & {{R}_{td}}={{R}_{1}}+{{R}_{2,3}}=20+15=35\Omega \\ & \Rightarrow I=\frac{U}{{{R}_{td}}}=\frac{25}{35}=\frac{5}{7}A \\ \end{align}$ $\begin{aligned} (1) & R_{t d} = R_{1} + R_{2, 3} = 20 + 15 = 35 Ω \\ (2) & \Rightarrow I = \frac{U}{R_{t d}} = \frac{25}{35} = \frac{5}{7} A \end{aligned}$

Do _{$R_{1} n t (R_{2} / / R_{3})$} nên _{$I = I_{1} = I_{2, 3} = I_{2} + I_{3} = \frac{5}{7} A$}

$\Rightarrow {{U}_{1}}={{I}_{1}}.{{R}_{1}}=\frac{5}{7}.20=\frac{100}{7}V$ $\Rightarrow U_{1} = I_{1} . R_{1} = \frac{5}{7} .20 = \frac{100}{7} V$

Ta lại có:

$\begin{align} & U={{U}_{1}}+{{U}_{2,3}} \\ & \Rightarrow {{U}_{2,3}}=U-{{U}_{1}}=25-\frac{100}{7}=\frac{75}{7}V \\ & \Rightarrow {{U}_{2}}={{U}_{3}}=\frac{75}{7}V\Rightarrow {{I}_{3}}=\frac{{{U}_{3}}}{{{R}_{3}}}=\frac{75/7}{30}=\frac{5}{14}A \\ \end{align}$ $\begin{aligned} (3) & U = U_{1} + U_{2, 3} \\ (4) & \Rightarrow U_{2, 3} = U - U_{1} = 25 - \frac{100}{7} = \frac{75}{7} V \\ (5) & \Rightarrow U_{2} = U_{3} = \frac{75}{7} V \Rightarrow I_{3} = \frac{U_{3}}{R_{3}} = \frac{75 / 7}{30} = \frac{5}{14} A \end{aligned}$

Bài tập 2: Khi mắc nối tiếp hai điện trở _{$R_{1}, R_{2}$} vào hiệu điện thế 12V thì dòng điện chạy qua chúng có cường độ _{$I = 0, 2 A$}

a. Tính điện trở tương đương của đoạn mạch nối tiếp này

b. Nếu mắc song song hai điện trở nói trên vào một hiệu điện thế thì dòng điện chạy qua điện trở _{$R_{1}$} có cường độ _{$I_{1}$} gấp 1,5 lần cường độ _{$I_{2}$} của dòng điện chạy qua điện trở _{$R_{2}$}. Hãy tính điện trở _{$R_{1}, R_{2}$}

Hướng dẫn giải

a. _{$R_{t d} = \frac{U}{I} = \frac{12}{0, 2} = 60 Ω$}

b. Nếu hai điện trở mắc song song với nhau _{$R_{t d} = \frac{R_{1} . R_{2}}{R_{1} + R_{2}} = \frac{U}{I} = 60 Ω$} (1)

_{$\frac{R_{1}}{R_{2}} = \frac{I_{2}}{I_{1}} = \frac{2}{3} \Rightarrow R_{1} = \frac{2}{3} R_{2}$} (2)

Từ (1) và (2) ta có: _{$R_{2} = 150 Ω, R_{1} = 100 Ω$}

Bài tập 3: Cho mạch điện như hình vẽ

Bài tập Vật lý 9 Bài 6: Bài tập vận dụng định luật Ôm

Trong đó: _{$R_{1} = 12 Ω, R_{2} = 24 Ω, R_{3} = 15 Ω$}, dòng điện đi qua _{$R_{1}$} có cường độ là ${{I}_{1}}=0,5A$ $I_{1} = 0, 5 A$

a. Tính các cường độ dòng điện _{$I_{2}, I_{3}$} tương ứng đi qua các điện trở _{$R_{2}, R_{3}$}

b. Tính các hiệu điện thế _{$U_{1}, U_{2}, U_{23}$}

Hướng dẫn giải

Ta có:

$\begin{align} & {{R}_{23}}=\frac{{{R}_{2}}.{{R}_{3}}}{{{R}_{2}}+{{R}_{3}}}=\frac{24.15}{24+15}=\frac{120}{13}\Omega \\ & \Rightarrow {{R}_{td}}={{R}_{1}}+{{R}_{23}}=12+\frac{120}{13}=\frac{276}{13}\Omega \\ \end{align}$ $\begin{aligned} (6) & R_{23} = \frac{R_{2} . R_{3}}{R_{2} + R_{3}} = \frac{24.15}{24 + 15} = \frac{120}{13} Ω \\ (7) & \Rightarrow R_{t d} = R_{1} + R_{23} = 12 + \frac{120}{13} = \frac{276}{13} Ω \end{aligned}$

$I={{I}_{1}}={{I}_{23}}=0.5A$ $I = I_{1} = I_{23} = 0.5 A$

$\begin{align} & \Rightarrow U=I.{{R}_{td}}=0,5.\frac{276}{13}=\frac{138}{13}V \\ & {{U}_{1}}={{I}_{1}}.{{R}_{1}}=0,5.12=6V\Rightarrow {{U}_{23}}={{U}_{2}}={{U}_{3}}=U-{{U}_{1}}=\frac{138}{13}-6=\frac{60}{13}V \\ & \Rightarrow {{I}_{2}}=\frac{{{U}_{2}}}{{{R}_{2}}}=\frac{60/13}{24}=\frac{5}{26}A \\ & \Rightarrow {{I}_{3}}=\frac{{{U}_{3}}}{{{R}_{3}}}=\frac{60/13}{15}=\frac{4}{13}A \\ \end{align}$ $\begin{aligned} (8) & \Rightarrow U = I . R_{t d} = 0, 5. \frac{276}{13} = \frac{138}{13} V \\ (9) & U_{1} = I_{1} . R_{1} = 0, 5.12 = 6 V \Rightarrow U_{23} = U_{2} = U_{3} = U - U_{1} = \frac{138}{13} - 6 = \frac{60}{13} V \\ (10) & \Rightarrow I_{2} = \frac{U_{2}}{R_{2}} = \frac{60 / 13}{24} = \frac{5}{26} A \\ (11) & \Rightarrow I_{3} = \frac{U_{3}}{R_{3}} = \frac{60 / 13}{15} = \frac{4}{13} A \end{aligned}$

Bài tâp 4: Cho mạch điện có: _{$R_{1} n t [(R_{2} n t R_{3}) / / R_{4}]$} biết _{$R_{1} = 15 Ω, R_{2} = 3 Ω, R_{3} = 7 Ω, R_{4} = 10 Ω$}, hiệu điện thế hau đầu đonạ mạch bằng 35V

a. Tính điện trở tương đương của đoạn mạch

b. Tìm cường độ dòng điện qua các điện trở

Hướng dẫn giải

${{R}_{234}}=\frac{\left( {{R}_{2}}+{{R}_{3}} \right).{{R}_{4}}}{\left( {{R}_{2}}+{{R}_{3}} \right)+{{R}_{4}}}=\frac{10.10}{10+10}=5\Omega$ $R_{234} = \frac{(R_{2} + R_{3}) . R_{4}}{(R_{2} + R_{3}) + R_{4}} = \frac{10.10}{10 + 10} = 5 Ω$

${{R}_{td}}={{R}_{1}}+{{R}_{234}}=15+5=20\Omega$ $R_{t d} = R_{1} + R_{234} = 15 + 5 = 20 Ω$

$\begin{align} & I={{I}_{1}}={{I}_{234}}={{I}_{23}}+{{I}_{4}}={{I}_{2}}+{{I}_{4}}={{I}_{3}}+{{I}_{4}}=\frac{U}{{{R}_{td}}}=\frac{35}{20}=1,75A \\ & \Rightarrow {{U}_{234}}={{U}_{23}}={{U}_{4}}={{I}_{234}}.{{R}_{234}}=1,75.5=8,75V \\ & \Rightarrow {{I}_{23}}=\frac{{{U}_{23}}}{{{R}_{23}}}=\frac{8,75}{{{R}_{2}}+{{R}_{3}}}=0,875A={{I}_{2}}={{I}_{3}} \\ & \Rightarrow {{I}_{4}}=\frac{{{U}_{4}}}{{{R}_{4}}}=\frac{8,75}{10}=0,875A \\ \end{align}$ $\begin{aligned} (12) & I = I_{1} = I_{234} = I_{23} + I_{4} = I_{2} + I_{4} = I_{3} + I_{4} = \frac{U}{R_{t d}} = \frac{35}{20} = 1, 75 A \\ (13) & \Rightarrow U_{234} = U_{23} = U_{4} = I_{234} . R_{234} = 1, 75.5 = 8, 75 V \\ (14) & \Rightarrow I_{23} = \frac{U_{23}}{R_{23}} = \frac{8, 75}{R_{2} + R_{3}} = 0, 875 A = I_{2} = I_{3} \\ (15) & \Rightarrow I_{4} = \frac{U_{4}}{R_{4}} = \frac{8, 75}{10} = 0, 875 A \end{aligned}$

-------------------------------------------------------

Xem thêm các bài Tìm bài trong mục này khác:

Chia sẻ, đánh giá bài viết

1

2.726

Bài trước

Bài sau

Chia sẻ bởi:
Nguyễn Thị Huê

Tải về

Chọn file muốn tải về:

Bài tập Vật lý 9 Bài 6: Bài tập vận dụng định luật Ôm

348,3 KB

Tải xuồng Word
219,5 KB

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

Tải tài liệu Trả phí + Miễn phí

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!