Đề thi học sinh giỏi lớp 9 THCS tỉnh Thanh Hóa năm 2014
Đề thi học sinh giỏi môn Toán lớp 9
Đề thi học sinh giỏi môn Toán lớp 9 năm học 2013 - 2014 tỉnh Thanh Hóa là đề thi học sinh giỏi lớp 9 môn Toán có đáp án được VnDoc sưu tầm và giới thiệu dành cho các em học sinh luyện đề, tự kiểm tra kiến thức cũng như ôn tập chuẩn bị cho kiểm tra cuối học kì 1 sắp tới. Mời các bạn cùng tham khảo.
Đề thi học sinh giỏi lớp 9 THCS tỉnh Quảng Ngãi năm 2014
SỞ GIÁO DỤC & ĐÀO TẠO
|
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH NĂM HỌC 2013-2014
|
Câu I (4,0 điểm): Cho biểu thức 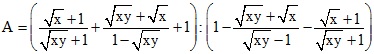
1. Rút gọn biểu thức A.
2. Cho ![]() . Tìm giá trị lớn nhất của A.
. Tìm giá trị lớn nhất của A.
Câu II (5,0 điểm).
1.Cho phương trình x2 + 2(m - 2)x + m2 - 2m + 4 = 0. Tìm m để phương trình có hai nghiệm thực phân biệt x1, x2 thỏa mãn![]()
2. Giải hệ phương trình ![]()
Câu III (4,0 điểm).
1. Tìm tất cả các cặp số nguyên dương (a; b) sao cho (a + b2) chia hết cho (a2b – 1).
2. Tìm x, y, z thuộc N thỏa mãn ![]() .
.
Câu IV (6,0 điểm):
Cho nửa đường tròn tâm O đường kính AB. Một điểm C cố định thuộc đoạn thẳng AO (C khác A và C khác O). Đường thẳng đi qua C và vuông góc với AO cắt nửa đường tròn đã cho tại D. Trên cung BD lấy điểm M (M khác B và M khác D). Tiếp tuyến của nửa đường tròn đã cho tại M cắt đường thẳng CD tại E. Gọi F là giao điểm của AM và CD.
1. Chứng minh tam giác EMF là tam giác cân.
2. Gọi I là tâm đường tròn ngoại tiếp tam giác FDM. Chứng minh ba điểm D, I, B thẳng hàng.
3. Chứng minh góc ABI có số đo không đổi khi M di chuyển trên cung BD.
Câu V (1,0 điểm): Cho x, y là các số thực dương thoả mãn x + y = 1.
Tìm giá trị nhỏ nhất của biểu thức ![]()



