VnDoc.com

Bộ 12 đề thi giữa kì 1 Toán 9 có đáp án

Đề kiểm tra giữa kì 1 Toán 9

Bài trước

Tải về

Bài sau

Lớp: Lớp 9

Dạng tài liệu: Đề thi

Loại: Tài liệu Lẻ

Loại File: ZIP

Phân loại: Tài liệu Tính phí

Đề kiểm tra giữa kì 1 Toán 9 có đáp án

Đề kiểm tra giữa kì 1 Toán 9 – Đề số 1
Đáp án đề thi giữa học kì 1 Toán 9 – Đề số 1
Đề thi giữa học kì 1 Toán 9 – Đề số 2
Đáp án đề kiểm tra giữa kì 1 Toán 9 – Đề số 2
Đề thi giữa học kì 1 Toán 9 – Đề số 3

Trong quá trình ôn tập cho kỳ thi giữa học kì 1, việc luyện đề là cách hiệu quả giúp học sinh lớp 9 rèn luyện kỹ năng giải toán, nắm chắc kiến thức và làm quen với cấu trúc đề thi. Hiểu được điều đó, chúng tôi tổng hợp Bộ 12 đề thi giữa kì 1 Toán 9 có đáp án nhằm hỗ trợ học sinh và giáo viên trong quá trình học tập và giảng dạy.

Các đề kiểm tra giữa kì 1 Toán 9 trong bộ tài liệu đều bám sát chương trình hiện hành, bao gồm các dạng toán trọng tâm như: căn bậc hai, phương trình bậc nhất, hệ thức lượng trong tam giác vuông,... Mỗi đề đều có đáp án chi tiết, giúp học sinh tự đánh giá mức độ hiểu bài và cải thiện kỹ năng giải đề. Tài liệu cũng rất phù hợp để giáo viên tham khảo ra đề kiểm tra giữa học kì cho lớp học của mình.

Đề kiểm tra giữa kì 1 Toán 9 – Đề số 1

Bài 1 (3 điểm): Cho biểu thức:

$P = \frac{{\sqrt x + 2}}{{\sqrt x - 3}} + \frac{{2\sqrt x }}{{\sqrt x + 3}} + \frac{{3x - 8\sqrt x + 27}}{{9 - x}}$ $P = \frac{{\sqrt x + 2}}{{\sqrt x - 3}} + \frac{{2\sqrt x }}{{\sqrt x + 3}} + \frac{{3x - 8\sqrt x + 27}}{{9 - x}}$

a) Tìm điều kiện của x để biểu thức P có nghĩa?

b) Rút gọn biểu thức.

c) Tìm giá trị x nguyên để P nhận giá trị nguyên.

Bài 2 (2 điểm): Tính giá trị của biểu thức:

a) $A = \sqrt {13 - 4\sqrt 3 } + \sqrt {13 + 4\sqrt 3 }$ $A = \sqrt {13 - 4\sqrt 3 } + \sqrt {13 + 4\sqrt 3 }$ b) $B = \frac{{2\sqrt 3 - 3\sqrt 2 }}{{\sqrt 6 }} + \frac{1}{{\sqrt 2 + \sqrt 3 }}$ $B = \frac{{2\sqrt 3 - 3\sqrt 2 }}{{\sqrt 6 }} + \frac{1}{{\sqrt 2 + \sqrt 3 }}$

Bài 3 (2 điểm): Giải phương trình:

a) ${x^2} - 4x - 45 = 0$ ${x^2} - 4x - 45 = 0$ b) $\frac{{3\sqrt x + 1}}{{x - 9}} = \frac{2}{{\sqrt x - 3}} - \frac{{\sqrt x - 3}}{{\sqrt x + 3}}$ $\frac{{3\sqrt x + 1}}{{x - 9}} = \frac{2}{{\sqrt x - 3}} - \frac{{\sqrt x - 3}}{{\sqrt x + 3}}$

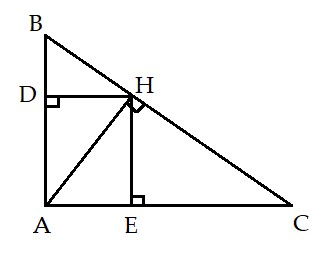
Bài 4 (3 điểm): Cho tam giác ABC (AB < AC) có $\widehat B + \widehat C = {90^0}$ $\widehat B + \widehat C = {90^0}$, AH là đường cao xuất phát từ đỉnh A (H ∈ BC). Gọi D là hình chiếu của H lên AB (D ∈ AB) và E là hình chiếu của H lên AC (E ∈ AC).

a) Chứng minh ADHE là hình chữ nhật.

b) Chứng minh AD.AB = AE.AC.

c) Biết AB = 6cm và AC = 8cm. Tính độ dài BC, AH, AD và AE.

Đáp án đề thi giữa học kì 1 Toán 9 – Đề số 1

Bài 1:

a) Để P có nghĩa _{$\Leftrightarrow \left\{ \begin{array}{l}
x \ge 0\\
x \ne 9
\end{array} \right.$}

b) $P = \frac{{\sqrt x + 2}}{{\sqrt x - 3}} + \frac{{2\sqrt x }}{{\sqrt x + 3}} + \frac{{3x - 8\sqrt x + 27}}{{9 - x}}$ $P = \frac{{\sqrt x + 2}}{{\sqrt x - 3}} + \frac{{2\sqrt x }}{{\sqrt x + 3}} + \frac{{3x - 8\sqrt x + 27}}{{9 - x}}$

$P = \frac{{\left( {\sqrt x + 2} \right)\left( {\sqrt x + 3} \right)}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}} + \frac{{2\sqrt x \left( {\sqrt x - 3} \right)}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}} - \frac{{3x - 8\sqrt x + 27}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}$ $P = \frac{{\left( {\sqrt x + 2} \right)\left( {\sqrt x + 3} \right)}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}} + \frac{{2\sqrt x \left( {\sqrt x - 3} \right)}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}} - \frac{{3x - 8\sqrt x + 27}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}$

$P = \frac{{x + 3\sqrt x + 2\sqrt x + 6 + 2x - 6\sqrt x - \left( {3x - 8\sqrt x + 27} \right)}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}$ $P = \frac{{x + 3\sqrt x + 2\sqrt x + 6 + 2x - 6\sqrt x - \left( {3x - 8\sqrt x + 27} \right)}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}$

$P = \frac{{7\sqrt x - 21}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}} = \frac{{7\left( {\sqrt x - 3} \right)}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}} = \frac{7}{{\sqrt x + 3}}$ $P = \frac{{7\sqrt x - 21}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}} = \frac{{7\left( {\sqrt x - 3} \right)}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}} = \frac{7}{{\sqrt x + 3}}$

Vậy $P = \frac{7}{{\sqrt x + 3}}$ $P = \frac{7}{{\sqrt x + 3}}$

c) Để P nhận giá trị nguyên

Ta có bảng:

$\sqrt x + 3$ $\sqrt x + 3$	- 7	- 1	1	7
$\sqrt x$ $\sqrt x$	- 10 (loại)	- 4 (loại)	- 2 (loại)	4
x				16 (tm)

Vậy để P nhận giá trị nguyên thì x = 16.

Bài 2:

a) $A = \sqrt {13 - 4\sqrt 3 } + \sqrt {13 + 4\sqrt 3 }$ $A = \sqrt {13 - 4\sqrt 3 } + \sqrt {13 + 4\sqrt 3 }$

$A = \sqrt {1 - 2.1.2\sqrt 3 + 12} + \sqrt {1 + 2.1.2\sqrt 3 + 12}$ $A = \sqrt {1 - 2.1.2\sqrt 3 + 12} + \sqrt {1 + 2.1.2\sqrt 3 + 12}$

$A = \sqrt {{{\left( {1 - 2\sqrt 3 } \right)}^2}} + \sqrt {{{\left( {1 + 2\sqrt 3 } \right)}^2}}$ $A = \sqrt {{{\left( {1 - 2\sqrt 3 } \right)}^2}} + \sqrt {{{\left( {1 + 2\sqrt 3 } \right)}^2}}$

$A = 2\sqrt 3 - 1 + 1 + 2\sqrt 3 = 4\sqrt 3$ $A = 2\sqrt 3 - 1 + 1 + 2\sqrt 3 = 4\sqrt 3$

b) $B = \frac{{2\sqrt 3 - 3\sqrt 2 }}{{\sqrt 6 }} + \frac{1}{{\sqrt 2 + \sqrt 3 }}$ $B = \frac{{2\sqrt 3 - 3\sqrt 2 }}{{\sqrt 6 }} + \frac{1}{{\sqrt 2 + \sqrt 3 }}$

$B = \frac{{\sqrt 6 \left( {\sqrt 2 - \sqrt 3 } \right)}}{{\sqrt 6 }} + \frac{1}{{\sqrt 2 + \sqrt 3 }}$ $B = \frac{{\sqrt 6 \left( {\sqrt 2 - \sqrt 3 } \right)}}{{\sqrt 6 }} + \frac{1}{{\sqrt 2 + \sqrt 3 }}$

$B = \sqrt 2 - \sqrt 3 + \frac{1}{{\sqrt 2 + \sqrt 3 }}$ $B = \sqrt 2 - \sqrt 3 + \frac{1}{{\sqrt 2 + \sqrt 3 }}$

$B = \frac{{\left( {\sqrt 2 - \sqrt 3 } \right)\left( {\sqrt 2 + \sqrt 3 } \right) + 1}}{{\sqrt 2 + \sqrt 3 }}$ $B = \frac{{\left( {\sqrt 2 - \sqrt 3 } \right)\left( {\sqrt 2 + \sqrt 3 } \right) + 1}}{{\sqrt 2 + \sqrt 3 }}$

$B = \frac{{\left( {2 - 3} \right) + 1}}{{\sqrt 2 + \sqrt 3 }} = \frac{{ - 1 + 1}}{{\sqrt 2 + \sqrt 3 }} = \frac{0}{{\sqrt 2 + \sqrt 3 }} = 0$ $B = \frac{{\left( {2 - 3} \right) + 1}}{{\sqrt 2 + \sqrt 3 }} = \frac{{ - 1 + 1}}{{\sqrt 2 + \sqrt 3 }} = \frac{0}{{\sqrt 2 + \sqrt 3 }} = 0$

Bài 3:

a) ${x^2} - 4x - 45 = 0$ ${x^2} - 4x - 45 = 0$

$\Leftrightarrow {x^2} - 9x + 5x - 45 = 0$ $\Leftrightarrow {x^2} - 9x + 5x - 45 = 0$

$\Leftrightarrow x\left( {x - 9} \right) + 5\left( {x - 9} \right) = 0$ $\Leftrightarrow x\left( {x - 9} \right) + 5\left( {x - 9} \right) = 0$

$\Leftrightarrow \left( {x + 5} \right)\left( {x - 9} \right) = 0 \Leftrightarrow \left[ \begin{array}{l} x + 5 = 0\\ x - 9 = 0 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = - 5\\ x = 9 \end{array} \right.$ $\Leftrightarrow \left( {x + 5} \right)\left( {x - 9} \right) = 0 \Leftrightarrow \left[ \begin{array}{l} x + 5 = 0\\ x - 9 = 0 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = - 5\\ x = 9 \end{array} \right.$

Vậy S = {-5; 9}

b) $\frac{{3\sqrt x + 1}}{{x - 9}} = \frac{2}{{\sqrt x - 3}} - \frac{{\sqrt x - 3}}{{\sqrt x + 3}}\left( {x \ge 0;x \ne 9} \right)$ $\frac{{3\sqrt x + 1}}{{x - 9}} = \frac{2}{{\sqrt x - 3}} - \frac{{\sqrt x - 3}}{{\sqrt x + 3}}\left( {x \ge 0;x \ne 9} \right)$

$\Leftrightarrow 3\sqrt x + 1 = 2\left( {\sqrt x + 3} \right) - \left( {\sqrt x - 3} \right)\left( {\sqrt x - 3} \right)$ $\Leftrightarrow 3\sqrt x + 1 = 2\left( {\sqrt x + 3} \right) - \left( {\sqrt x - 3} \right)\left( {\sqrt x - 3} \right)$

$\Leftrightarrow 3\sqrt x + 1 = 2\sqrt x + 6 - \left( {x - 6\sqrt x + 9} \right)$ $\Leftrightarrow 3\sqrt x + 1 = 2\sqrt x + 6 - \left( {x - 6\sqrt x + 9} \right)$

$\Leftrightarrow 3\sqrt x + 1 = 2\sqrt x + 6 - x + 6\sqrt x - 9$ $\Leftrightarrow 3\sqrt x + 1 = 2\sqrt x + 6 - x + 6\sqrt x - 9$

$\Leftrightarrow x - 5\sqrt x + 4 = 0$ $\Leftrightarrow x - 5\sqrt x + 4 = 0$

$\Leftrightarrow x - \sqrt x - 4\sqrt x + 4 = 0$ $\Leftrightarrow x - \sqrt x - 4\sqrt x + 4 = 0$

$\Leftrightarrow \sqrt x \left( {\sqrt x - 1} \right) - 4\left( {\sqrt x - 1} \right) = 0$ $\Leftrightarrow \sqrt x \left( {\sqrt x - 1} \right) - 4\left( {\sqrt x - 1} \right) = 0$

$\Leftrightarrow \left( {\sqrt x - 4} \right)\left( {\sqrt x - 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l} \sqrt x = 4\\ \sqrt x = 1 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = 16\\ x = 1 \end{array} \right.\left( {tm} \right)$ $\Leftrightarrow \left( {\sqrt x - 4} \right)\left( {\sqrt x - 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l} \sqrt x = 4\\ \sqrt x = 1 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = 16\\ x = 1 \end{array} \right.\left( {tm} \right)$

Vậy S = {1; 16}

Bài 4:

Đề thi giữa học kì 1 Toán 9 năm học 2020 - 2021 - Đề 1

a) + Xét tam giác ABC có: $\widehat A + \widehat B + \widehat C = {180^0}$ $\widehat A + \widehat B + \widehat C = {180^0}$(tổng ba góc trong tam giác)

mà $\widehat B + \widehat C = {90^0} \Rightarrow \widehat A = {90^0}$ $\widehat B + \widehat C = {90^0} \Rightarrow \widehat A = {90^0}$

+ Xét tứ giác ADHE có:

$\widehat {DAE} = {90^0}$ $\widehat {DAE} = {90^0}$(cmt)

$\widehat {HDA} = {90^0}$ $\widehat {HDA} = {90^0}$( $HD \bot AB$ $HD \bot AB$ - gt)

$\widehat {HEA} = {90^0}$ $\widehat {HEA} = {90^0}$( $HE \bot AC$ $HE \bot AC$ - gt)

$\Rightarrow$ $\Rightarrow$ADHE là hình chữ nhật (dhnb) (đpcm)

b) + Xét tam giác ABH có $\widehat {AHB} = {90^0};HD \bot AB$ $\widehat {AHB} = {90^0};HD \bot AB$:

$A{H^2} = AD.AB$ $A{H^2} = AD.AB$(hệ thức lượng trong tam giác vuông) (1)

+ Xét tam giác AHC có $\widehat {AHC} = {90^0};HE \bot AC$ $\widehat {AHC} = {90^0};HE \bot AC$:

$A{H^2} = AE.AC$ $A{H^2} = AE.AC$(hệ thức lượng trong tam giác vuông) (2)

+ Từ (1) và (2) $\Rightarrow AD.AB = AE.AC\left( { = A{H^2}} \right)$ $\Rightarrow AD.AB = AE.AC\left( { = A{H^2}} \right)$(đpcm)

c) + Xét tam giác ABC có $\widehat {BAC} = {90^0};AH \bot BC$ $\widehat {BAC} = {90^0};AH \bot BC$:

$A{B^2} + A{C^2} = B{C^2}$ $A{B^2} + A{C^2} = B{C^2}$(Pitago)

$\Rightarrow BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {100} = 10$ $\Rightarrow BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {100} = 10$(cm)

$\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}$ $\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}$(hệ thức lượng trong tam giác vuông)

$\Rightarrow AH = \sqrt {\frac{{A{B^2}.A{C^2}}}{{A{B^2} + A{C^2}}}} = \frac{{24}}{5}$ $\Rightarrow AH = \sqrt {\frac{{A{B^2}.A{C^2}}}{{A{B^2} + A{C^2}}}} = \frac{{24}}{5}$(cm)

+ Từ (1) $\Rightarrow AD = \frac{{A{H^2}}}{{AB}} = \frac{{96}}{{25}}$ $\Rightarrow AD = \frac{{A{H^2}}}{{AB}} = \frac{{96}}{{25}}$(cm)

+ Từ (2) $\Rightarrow AE = \frac{{A{H^2}}}{{AC}} = \frac{{72}}{{25}}$ $\Rightarrow AE = \frac{{A{H^2}}}{{AC}} = \frac{{72}}{{25}}$(cm)

Đề thi giữa học kì 1 Toán 9 – Đề số 2

Bài 1 (1 điểm): Tìm điều kiện để các căn thức dưới đây có nghĩa:

a) $\sqrt {16 - 4x}$ $\sqrt {16 - 4x}$

b) $\sqrt {3x + 7}$ $\sqrt {3x + 7}$

Bài 2 (2 điểm): Rút gọn các biểu thức dưới đây:

a) $A = \sqrt {72} - \sqrt 4 .\frac{1}{2} + \sqrt {32} + \sqrt {162}$ $A = \sqrt {72} - \sqrt 4 .\frac{1}{2} + \sqrt {32} + \sqrt {162}$

b) $B = \frac{1}{{\sqrt 7 - 4}} + \frac{1}{{\sqrt 7 + 4}}$ $B = \frac{1}{{\sqrt 7 - 4}} + \frac{1}{{\sqrt 7 + 4}}$

Bài 3 (2 điểm): Cho hai biểu thức $M = \frac{1}{{\sqrt x - \sqrt {x - 1} }} - \frac{1}{{\sqrt x + \sqrt {x - 1} }}$ $M = \frac{1}{{\sqrt x - \sqrt {x - 1} }} - \frac{1}{{\sqrt x + \sqrt {x - 1} }}$và $N = \frac{{\sqrt {x - 1} }}{{\sqrt x - 5}}$ $N = \frac{{\sqrt {x - 1} }}{{\sqrt x - 5}}$

a) Rút gọn biểu thức P = M:N.

b) Tính giá trị của biểu thức P tại $x = 4 - 2\sqrt 3$ $x = 4 - 2\sqrt 3$.

Bài 4 (2 điểm): Giải phương trình:

a) ${x^2} - 8x - 9 = 0$ ${x^2} - 8x - 9 = 0$

b) $\sqrt {5x + 4} = x + 2$ $\sqrt {5x + 4} = x + 2$

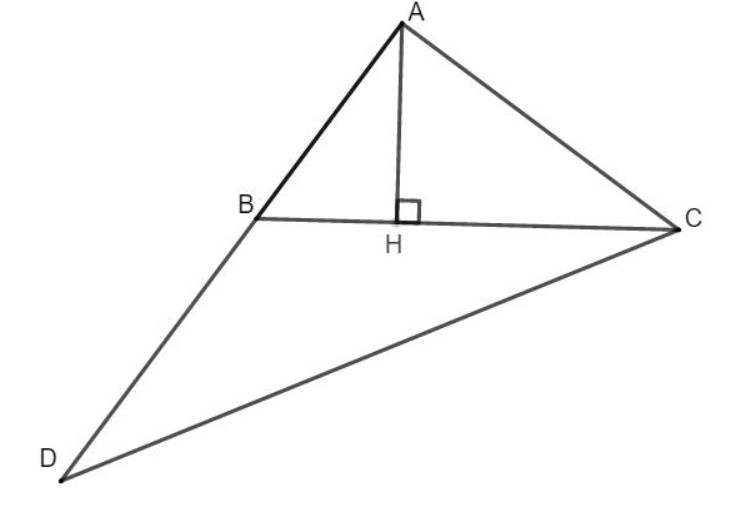
Bài 5 (3 điểm): Cho tam giác ABC có AB = 6cm, AC = 8cm, BC = 10cm.

a) Chứng minh tam giác ABC là tam giác vuông.

b) Vẽ đường cao AH (H ∈ BC). Tính độ dài của BH, HC và AH.

c) Trên tia đối của tia BA, lấy điểm D sao cho BD = BC. Chứng minh: ${\mathop{\rm AD}\nolimits} .BC = \frac{{{{{\mathop{\rm CD}\nolimits} }^2}}}{2}$ ${\mathop{\rm AD}\nolimits} .BC = \frac{{{{{\mathop{\rm CD}\nolimits} }^2}}}{2}$

d) Tính diện tích tam giác BCD

Đáp án đề kiểm tra giữa kì 1 Toán 9 – Đề số 2

Bài 1:

a) Để biểu thức $\sqrt {16 - 4x}$ $\sqrt {16 - 4x}$ có nghĩa thì $16 - 4x \ge 0 \Leftrightarrow x \le 4$ $16 - 4x \ge 0 \Leftrightarrow x \le 4$.

b) Để biểu thức $\sqrt {3x + 7}$ $\sqrt {3x + 7}$ có nghĩa thì $3x + 7 \ge 0 \Leftrightarrow x \ge \frac{{ - 7}}{3}$ $3x + 7 \ge 0 \Leftrightarrow x \ge \frac{{ - 7}}{3}$.

Bài 2:

a) $A = \sqrt {72} - \sqrt 4 .\frac{1}{2} + \sqrt {32} + \sqrt {162}$ $A = \sqrt {72} - \sqrt 4 .\frac{1}{2} + \sqrt {32} + \sqrt {162}$

$A = \sqrt {36.2} - 2.\frac{1}{2} + \sqrt {16.2} + \sqrt {81.2}$ $A = \sqrt {36.2} - 2.\frac{1}{2} + \sqrt {16.2} + \sqrt {81.2}$

$A = 6\sqrt 2 - 1 + 4\sqrt 2 + 9\sqrt 2$ $A = 6\sqrt 2 - 1 + 4\sqrt 2 + 9\sqrt 2$

$A = 19\sqrt 2 - 1$ $A = 19\sqrt 2 - 1$

b) $B = \frac{1}{{\sqrt 7 - 4}} + \frac{1}{{\sqrt 7 + 4}} = \frac{{\sqrt 7 + 4 + \sqrt 7 - 4}}{{\left( {\sqrt 7 - 4} \right)\left( {\sqrt 7 + 4} \right)}} = \frac{{2\sqrt 7 }}{{7 - 16}} = \frac{{2\sqrt 7 }}{{ - 9}} = \frac{{ - 2\sqrt 7 }}{9}$ $B = \frac{1}{{\sqrt 7 - 4}} + \frac{1}{{\sqrt 7 + 4}} = \frac{{\sqrt 7 + 4 + \sqrt 7 - 4}}{{\left( {\sqrt 7 - 4} \right)\left( {\sqrt 7 + 4} \right)}} = \frac{{2\sqrt 7 }}{{7 - 16}} = \frac{{2\sqrt 7 }}{{ - 9}} = \frac{{ - 2\sqrt 7 }}{9}$

Bài 3:

a) $M = \frac{1}{{\sqrt x - \sqrt {x - 1} }} - \frac{1}{{\sqrt x + \sqrt {x - 1} }}$ $M = \frac{1}{{\sqrt x - \sqrt {x - 1} }} - \frac{1}{{\sqrt x + \sqrt {x - 1} }}$; điều kiện $x \ge 1$ $x \ge 1$

$M = \frac{{\sqrt x + \sqrt {x - 1} - \left( {\sqrt x - \sqrt {x - 1} } \right)}}{{\left( {\sqrt x - \sqrt {x - 1} } \right)\left( {\sqrt x + \sqrt {x - 1} } \right)}} = \frac{{2\sqrt {x - 1} }}{{x - \left( {x - 1} \right)}} = 2\sqrt {x - 1}$ $M = \frac{{\sqrt x + \sqrt {x - 1} - \left( {\sqrt x - \sqrt {x - 1} } \right)}}{{\left( {\sqrt x - \sqrt {x - 1} } \right)\left( {\sqrt x + \sqrt {x - 1} } \right)}} = \frac{{2\sqrt {x - 1} }}{{x - \left( {x - 1} \right)}} = 2\sqrt {x - 1}$

$N = \frac{{\sqrt {x - 1} }}{{\sqrt x - 5}}$ $N = \frac{{\sqrt {x - 1} }}{{\sqrt x - 5}}$; điều kiện $x \ge 0;x \ne 25$ $x \ge 0;x \ne 25$

$P = M:N = 2\sqrt {x - 1} .\frac{{\sqrt x - 5}}{{\sqrt {x - 1} }} = 2\left( {\sqrt x - 5} \right)$ $P = M:N = 2\sqrt {x - 1} .\frac{{\sqrt x - 5}}{{\sqrt {x - 1} }} = 2\left( {\sqrt x - 5} \right)$

Vậy $P = 2\left( {\sqrt x - 5} \right)$ $P = 2\left( {\sqrt x - 5} \right)$

b) Tại $x = 4 - 2\sqrt 3$ $x = 4 - 2\sqrt 3$(tm) thì $\sqrt x = \sqrt {4 - 2\sqrt 3 } = \sqrt {{{\left( {\sqrt 3 - 1} \right)}^2}} = \sqrt 3 - 1$ $\sqrt x = \sqrt {4 - 2\sqrt 3 } = \sqrt {{{\left( {\sqrt 3 - 1} \right)}^2}} = \sqrt 3 - 1$

Có $P = 2\left( {\sqrt 3 - 1 - 5} \right) = 2\left( {\sqrt 3 - 6} \right) = 2\sqrt 3 - 12$ $P = 2\left( {\sqrt 3 - 1 - 5} \right) = 2\left( {\sqrt 3 - 6} \right) = 2\sqrt 3 - 12$

Vậy tại $x = 4 - 2\sqrt 3$ $x = 4 - 2\sqrt 3$ thì $P = 2\sqrt 3 - 12$ $P = 2\sqrt 3 - 12$

Bài 4:

a) ${x^2} - 8x - 9 = 0$ ${x^2} - 8x - 9 = 0$

$\Leftrightarrow {x^2} + x - 9x - 9 = 0$ $\Leftrightarrow {x^2} + x - 9x - 9 = 0$

$\Leftrightarrow x\left( {x + 1} \right) - 9\left( {x + 1} \right) = 0$ $\Leftrightarrow x\left( {x + 1} \right) - 9\left( {x + 1} \right) = 0$

$\Leftrightarrow \left( {x - 9} \right)\left( {x + 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l} x = 9\\ x = - 1 \end{array} \right.$ $\Leftrightarrow \left( {x - 9} \right)\left( {x + 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l} x = 9\\ x = - 1 \end{array} \right.$

Vậy S = {-1; 9}

b) $\sqrt {5x + 4} = x + 2$ $\sqrt {5x + 4} = x + 2$(1)

Điều kiện $5x + 4 \ge 0 \Leftrightarrow x \ge \frac{{ - 4}}{5}$ $5x + 4 \ge 0 \Leftrightarrow x \ge \frac{{ - 4}}{5}$

(1) $\Leftrightarrow \left\{ \begin{array}{l} x + 2 \ge 0\\ 5x + 4 = {\left( {x + 2} \right)^2} \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x \ge - 2\\ 5x + 4 = {x^2} + 4x + 4 \end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l} x + 2 \ge 0\\ 5x + 4 = {\left( {x + 2} \right)^2} \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x \ge - 2\\ 5x + 4 = {x^2} + 4x + 4 \end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l} x \ge - 2\\ {x^2} - x = 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x \ge - 2\\ \left[ \begin{array}{l} x = 0\\ x = 1 \end{array} \right.\left( {tm} \right) \end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l} x \ge - 2\\ {x^2} - x = 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x \ge - 2\\ \left[ \begin{array}{l} x = 0\\ x = 1 \end{array} \right.\left( {tm} \right) \end{array} \right.$

Vậy S = {0; 1}

Bài 4:

Đề thi giữa học kì 1 Toán 9 năm học 2020 - 2021 - Đề 2

a) Xét ∆ABC có:

$\left. \begin{array}{l} {{\mathop{\rm AB}\nolimits} ^2} + {{\mathop{\rm AC}\nolimits} ^2} = {6^2} + {8^2} = 100\\ {{\mathop{\rm BC}\nolimits} ^2} = {10^2} = 100 \end{array} \right\} \Rightarrow {{\mathop{\rm AB}\nolimits} ^2} + {{\mathop{\rm AC}\nolimits} ^2} = {{\mathop{\rm BC}\nolimits} ^2}$ $\left. \begin{array}{l} {{\mathop{\rm AB}\nolimits} ^2} + {{\mathop{\rm AC}\nolimits} ^2} = {6^2} + {8^2} = 100\\ {{\mathop{\rm BC}\nolimits} ^2} = {10^2} = 100 \end{array} \right\} \Rightarrow {{\mathop{\rm AB}\nolimits} ^2} + {{\mathop{\rm AC}\nolimits} ^2} = {{\mathop{\rm BC}\nolimits} ^2}$

⇒ABC vuông tại A (Pitago đảo)

b) Xét ∆ABC vuông tại A(cmt), có AH ⊥ BC:

+ ${{\mathop{\rm AB}\nolimits} ^2} = {\mathop{\rm BH}\nolimits} .BC$ ${{\mathop{\rm AB}\nolimits} ^2} = {\mathop{\rm BH}\nolimits} .BC$(hệ thức lượng trong tam giác vuông)

$\Rightarrow {\mathop{\rm BH}\nolimits} = \frac{{{{{\mathop{\rm AB}\nolimits} }^2}}}{{{\mathop{\rm BC}\nolimits} }} = \frac{{36}}{{100}} = \frac{9}{{25}}$ $\Rightarrow {\mathop{\rm BH}\nolimits} = \frac{{{{{\mathop{\rm AB}\nolimits} }^2}}}{{{\mathop{\rm BC}\nolimits} }} = \frac{{36}}{{100}} = \frac{9}{{25}}$(cm)

+ ${{\mathop{\rm AC}\nolimits} ^2} = {\mathop{\rm CH}\nolimits} .CB$ ${{\mathop{\rm AC}\nolimits} ^2} = {\mathop{\rm CH}\nolimits} .CB$(hệ thức lượng trong tam giác vuông)

$\Rightarrow {\mathop{\rm CH}\nolimits} = \frac{{{{{\mathop{\rm AC}\nolimits} }^2}}}{{{\mathop{\rm BC}\nolimits} }} = \frac{{64}}{{100}} = \frac{{16}}{{25}}$ $\Rightarrow {\mathop{\rm CH}\nolimits} = \frac{{{{{\mathop{\rm AC}\nolimits} }^2}}}{{{\mathop{\rm BC}\nolimits} }} = \frac{{64}}{{100}} = \frac{{16}}{{25}}$(cm)

+ ${{\mathop{\rm AH}\nolimits} ^2} = {\mathop{\rm BH}\nolimits} .HC$ ${{\mathop{\rm AH}\nolimits} ^2} = {\mathop{\rm BH}\nolimits} .HC$(hệ thức lượng trong tam giác vuông)

$\Rightarrow {{\mathop{\rm AB}\nolimits} ^2} = \frac{9}{{25}}.\frac{{16}}{{25}} \Rightarrow {\mathop{\rm AB}\nolimits} = \frac{{12}}{{25}}$ $\Rightarrow {{\mathop{\rm AB}\nolimits} ^2} = \frac{9}{{25}}.\frac{{16}}{{25}} \Rightarrow {\mathop{\rm AB}\nolimits} = \frac{{12}}{{25}}$(cm)

c) + Có AD = AB + BD = 6 + 10 = 16 (cm)

+ Xét ∆ADC vuông tại A có:

${{\mathop{\rm AD}\nolimits} ^2} + {{\mathop{\rm AC}\nolimits} ^2} = {{\mathop{\rm CD}\nolimits} ^2}$ ${{\mathop{\rm AD}\nolimits} ^2} + {{\mathop{\rm AC}\nolimits} ^2} = {{\mathop{\rm CD}\nolimits} ^2}$(Pitago)

$\Rightarrow {\mathop{\rm CD}\nolimits} = \sqrt {{{16}^2} + {8^2}} = 8\sqrt 5$ $\Rightarrow {\mathop{\rm CD}\nolimits} = \sqrt {{{16}^2} + {8^2}} = 8\sqrt 5$(cm)

+ Có AD.BC = 16.10 = 160

Và $\frac{{C{D^2}}}{2} = \frac{{320}}{2} = 160$ $\frac{{C{D^2}}}{2} = \frac{{320}}{2} = 160$

Vậy ${\mathop{\rm AD}\nolimits} .BC = \frac{{C{D^2}}}{2}$ ${\mathop{\rm AD}\nolimits} .BC = \frac{{C{D^2}}}{2}$

d) + ${{\mathop{\rm S}\nolimits} _{\Delta ABC}} = \frac{1}{2}{\mathop{\rm AB}\nolimits} .AC = \frac{1}{2}.6.8 = 24$ ${{\mathop{\rm S}\nolimits} _{\Delta ABC}} = \frac{1}{2}{\mathop{\rm AB}\nolimits} .AC = \frac{1}{2}.6.8 = 24$ (cm²)

+ ${{\mathop{\rm S}\nolimits} _{\Delta {\mathop{\rm ACD}\nolimits} }} = \frac{1}{2}{\mathop{\rm A}\nolimits} {\mathop{\rm D}\nolimits} .AC = \frac{1}{2}.16.8 = 64$ ${{\mathop{\rm S}\nolimits} _{\Delta {\mathop{\rm ACD}\nolimits} }} = \frac{1}{2}{\mathop{\rm A}\nolimits} {\mathop{\rm D}\nolimits} .AC = \frac{1}{2}.16.8 = 64$(cm²)

Vậy S_∆BCD = 64 – 24 = 40 (cm²).

Đề thi giữa học kì 1 Toán 9 – Đề số 3

I. TRẮC NGHIỆM. (5 điểm) Học sinh điền các đáp án chọn tương ứng vào bảng kết quả dưới đây:

Câu	1	2	3	4	5	6	7	8	9	10
Trả lời

Câu 1. Căn bậc hai số học của 49 là:

A. -7 B. 7 C. $\pm 7$ $\pm 7$ D. 7²

Câu 2. Khai phương tích 12.30.40 được kết quả là:

A. 1200 B. 120 C. 12 D. 240

Câu 3. Nếu $\sqrt{16x} - \sqrt{9x} = 2$ $\sqrt{16x} - \sqrt{9x} = 2$ thì x bằng:

A. 4 B. 2 C. $\frac{4}{7}$ $\frac{4}{7}$ D. một kết quả khác

Câu 4. Biểu thức $\sqrt{2 - 3x}$ $\sqrt{2 - 3x}$ xác định với các giá trị:

A. $x \geq \frac{2}{3}$ $x \geq \frac{2}{3}$ B. $x \geq - \frac{2}{3}$ $x \geq - \frac{2}{3}$ C. $x \leq \frac{2}{3}$ $x \leq \frac{2}{3}$ D. $x \leq - \frac{2}{3}$ $x \leq - \frac{2}{3}$

Câu 5. Biểu thức $\sqrt{(\sqrt{3} - 2)^{2}}$ $\sqrt{(\sqrt{3} - 2)^{2}}$ có giá trị là:

A. 1 B. -1 C. $\sqrt{3} - 2$ $\sqrt{3} - 2$ D. $2 - \sqrt{3}$ $2 - \sqrt{3}$

Câu 6. Giá trị của biểu thức $\frac{1}{2 + \sqrt{3}} + \frac{1}{2 - \sqrt{3}}$ $\frac{1}{2 + \sqrt{3}} + \frac{1}{2 - \sqrt{3}}$ bằng:

A. $\frac{1}{2}$ $\frac{1}{2}$ B. 1 C. $- 4$ D. 4

Câu 7. Biểu thức $2y^{2}\sqrt{\frac{x^{4}}{4y^{2}}}$ $2y^{2}\sqrt{\frac{x^{4}}{4y^{2}}}$ với y < 0 được rút gọn là:

A. – xy² B. $\frac{y^{2}x^{2}}{|y|}$ $\frac{y^{2}x^{2}}{|y|}$ C. – x²y D. $\sqrt{y^{2}x^{4}}$ $\sqrt{y^{2}x^{4}}$

Câu 8. Cho $\alpha = 35^{0};\ \ \beta = 55^{0}$ $\alpha = 35^{0};\ \ \beta = 55^{0}$. Khẳng định nào sau đây là sai?

A. $\sin\alpha = \sin\beta$ $\sin\alpha = \sin\beta$. B. $\sin\alpha = cos\beta$ $\sin\alpha = cos\beta$.

C. $\tan\alpha = \cot\beta$ $\tan\alpha = \cot\beta$. D. $cos\alpha = sin\beta$ $cos\alpha = sin\beta$.

Câu 9. Cho $cos^{2}\alpha = \frac{4}{9}$ $cos^{2}\alpha = \frac{4}{9}$, khi đó sin $\alpha$ $\alpha$ bằng:

A. $\frac{5}{9}$ $\frac{5}{9}$. B. $\frac{\sqrt{5}}{3}$ $\frac{\sqrt{5}}{3}$. C. $\frac{1}{3}$ $\frac{1}{3}$. D. $\frac{1}{2}$ $\frac{1}{2}$.

Câu 10. Trong $\Delta$ $\Delta$ABC vuông tại A có AC = 3a; AB = $3\sqrt{3}a$ $3\sqrt{3}a$, khi đó góc B bằng:

A. 90⁰. B. 60⁰. C. 45⁰. D. 30⁰.

II. TỰ LUẬN. (5 điểm)

Bài 1. (1,0 điểm)

a) Thực hiện phép tính: $\left( \sqrt{50} - 2\sqrt{18} + \sqrt{98} \right):\ \sqrt{2}$ $\left( \sqrt{50} - 2\sqrt{18} + \sqrt{98} \right):\ \sqrt{2}$.

b) So sánh: $2\sqrt 3 + 1$ $2\sqrt 3 + 1$ và $2\sqrt 2 + 5$ $2\sqrt 2 + 5$.

Bài 2. (2 điểm) Cho biểu thức $A\ = \ \left( \frac{a\ - \ \sqrt{a}}{\sqrt{a\ } - \ 1}\ - \ \frac{\sqrt{a}\ + \ 1}{a\ + \ \sqrt{a}} \right)\ :\ \left( 1\ - \ \frac{1}{a} \right)$ $A\ = \ \left( \frac{a\ - \ \sqrt{a}}{\sqrt{a\ } - \ 1}\ - \ \frac{\sqrt{a}\ + \ 1}{a\ + \ \sqrt{a}} \right)\ :\ \left( 1\ - \ \frac{1}{a} \right)$

a) Tìm điều kiện xác định của A.

b) Rút gọn A.

Bài 3. (2 điểm) Cho tam giác ABC vuông tại A, AB = 3(cm), AC = 4(cm)

a) Giải tam giác vuông ABC (góc làm tròn đến phút).

b) Kẽ đường cao AH, gọi K là hình chiếu của H trên AC, G là hình chiếu của H trên AB. Chứng minh $\frac{AB}{AC}\ = \ \frac{AK}{AG}$ $\frac{AB}{AC}\ = \ \frac{AK}{AG}$.

Bạn muốn xem toàn bộ tài liệu? Hãy nhấn Tải về ngay!

-----------------------------------------------------------------

Bộ 12 đề thi giữa kì 1 Toán 9 có đáp án mà chúng tôi chia sẻ sẽ là tài liệu luyện tập hiệu quả giúp học sinh lớp 9 nâng cao tư duy, rèn luyện kỹ năng giải toán và chuẩn bị vững vàng cho kỳ thi giữa học kì.

Mỗi đề thi không chỉ giúp học sinh kiểm tra kiến thức Toán 9 đã học mà còn làm quen với cách trình bày bài thi đúng chuẩn. Ngoài ra, bộ đề cũng là công cụ hữu ích để giáo viên tham khảo xây dựng đề kiểm tra phù hợp với năng lực học sinh.

Đừng quên lưu lại và chia sẻ tài liệu này để cùng bạn bè ôn tập hiệu quả hơn. Theo dõi website của chúng tôi để cập nhật thêm nhiều bộ đề kiểm tra Toán 9 hay, bám sát chương trình, có đáp án và hướng dẫn giải chi tiết.

Tải về

Chọn file muốn tải về: