Đề thi giữa kì 1 Toán 9 năm 2023 - Đề 1

Đề kiểm tra giữa kì 1 Toán 9 có đáp án

Đề thi giữa học kì 1 Toán 9 năm học 2022 - 2023

Đề kiểm tra giữa kì 1 Toán 9 – Đề số 1
Đáp án đề thi giữa học kì 1 Toán 9 – Đề số 1

Đề thi giữa kì 1 Toán 9 năm 2023 được VnDoc biên soạn có đầy đủ đáp án cho các bạn học sinh tham khảo. Đề kiểm tra giữa kì 1 Toán 9 bao gồm 4 câu hỏi tự luận có đáp án, cho các em luyện tập, so sánh và đối chiếu với bài làm của mình, giúp các em rèn luyện kỹ năng giải Toán, chuẩn bị cho bài thi giữa học kì 1 lớp 9 đạt kết quả cao. Mời các em học sinh tham khảo chi tiết.

Tham khảo thêm: Đề thi giữa học kì 1 lớp 9 môn Toán - Đề số 2

Bản quyền thuộc về VnDoc.
Nghiêm cấm mọi hình thức sao chép nhằm mục đích thương mại.

Đề kiểm tra giữa kì 1 Toán 9 – Đề số 1

Bài 1 (3 điểm): Cho biểu thức:

$P = \frac{{\sqrt x + 2}}{{\sqrt x - 3}} + \frac{{2\sqrt x }}{{\sqrt x + 3}} + \frac{{3x - 8\sqrt x + 27}}{{9 - x}}$ $P = \frac{{\sqrt x + 2}}{{\sqrt x - 3}} + \frac{{2\sqrt x }}{{\sqrt x + 3}} + \frac{{3x - 8\sqrt x + 27}}{{9 - x}}$

a) Tìm điều kiện của x để biểu thức P có nghĩa?

b) Rút gọn biểu thức

c) Tìm giá trị x nguyên để P nhận giá trị nguyên

Bài 2 (2 điểm): Tính giá trị của biểu thức:

a) $A = \sqrt {13 - 4\sqrt 3 } + \sqrt {13 + 4\sqrt 3 }$ $A = \sqrt {13 - 4\sqrt 3 } + \sqrt {13 + 4\sqrt 3 }$

b) $B = \frac{{2\sqrt 3 - 3\sqrt 2 }}{{\sqrt 6 }} + \frac{1}{{\sqrt 2 + \sqrt 3 }}$ $B = \frac{{2\sqrt 3 - 3\sqrt 2 }}{{\sqrt 6 }} + \frac{1}{{\sqrt 2 + \sqrt 3 }}$

Bài 3 (2 điểm): Giải phương trình:

a) ${x^2} - 4x - 45 = 0$ ${x^2} - 4x - 45 = 0$

b) $\frac{{3\sqrt x + 1}}{{x - 9}} = \frac{2}{{\sqrt x - 3}} - \frac{{\sqrt x - 3}}{{\sqrt x + 3}}$ $\frac{{3\sqrt x + 1}}{{x - 9}} = \frac{2}{{\sqrt x - 3}} - \frac{{\sqrt x - 3}}{{\sqrt x + 3}}$

Bài 4 (3 điểm): Cho tam giác ABC (AB < AC) có $\widehat B + \widehat C = {90^0}$ $\widehat B + \widehat C = {90^0}$, AH là đường cao xuất phát từ đỉnh A (H ∈ BC). Gọi D là hình chiếu của H lên AB (D ∈ AB) và E là hình chiếu của H lên AC (E ∈ AC).

a) Chứng minh ADHE là hình chữ nhật

b) Chứng minh AD.AB = AE.AC

c) Biết AB = 6cm và AC = 8cm. Tính độ dài BC, AH, AD và AE

Đáp án đề thi giữa học kì 1 Toán 9 – Đề số 1

Bài 1:

a) Để P có nghĩa _{$\Leftrightarrow \left\{ \begin{array}{l} x \ge 0\\ x \ne 9 \end{array} \right.$}

b) $P = \frac{{\sqrt x + 2}}{{\sqrt x - 3}} + \frac{{2\sqrt x }}{{\sqrt x + 3}} + \frac{{3x - 8\sqrt x + 27}}{{9 - x}}$ $P = \frac{{\sqrt x + 2}}{{\sqrt x - 3}} + \frac{{2\sqrt x }}{{\sqrt x + 3}} + \frac{{3x - 8\sqrt x + 27}}{{9 - x}}$

$P = \frac{{\left( {\sqrt x + 2} \right)\left( {\sqrt x + 3} \right)}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}} + \frac{{2\sqrt x \left( {\sqrt x - 3} \right)}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}} - \frac{{3x - 8\sqrt x + 27}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}$ $P = \frac{{\left( {\sqrt x + 2} \right)\left( {\sqrt x + 3} \right)}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}} + \frac{{2\sqrt x \left( {\sqrt x - 3} \right)}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}} - \frac{{3x - 8\sqrt x + 27}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}$

$P = \frac{{x + 3\sqrt x + 2\sqrt x + 6 + 2x - 6\sqrt x - \left( {3x - 8\sqrt x + 27} \right)}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}$ $P = \frac{{x + 3\sqrt x + 2\sqrt x + 6 + 2x - 6\sqrt x - \left( {3x - 8\sqrt x + 27} \right)}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}$

$P = \frac{{7\sqrt x - 21}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}} = \frac{{7\left( {\sqrt x - 3} \right)}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}} = \frac{7}{{\sqrt x + 3}}$ $P = \frac{{7\sqrt x - 21}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}} = \frac{{7\left( {\sqrt x - 3} \right)}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}} = \frac{7}{{\sqrt x + 3}}$

Vậy $P = \frac{7}{{\sqrt x + 3}}$ $P = \frac{7}{{\sqrt x + 3}}$

c) Để P nhận giá trị nguyên

Ta có bảng:

$\sqrt x + 3$ $\sqrt x + 3$	- 7	- 1	1	7
$\sqrt x$ $\sqrt x$	- 10 (loại)	- 4 (loại)	- 2 (loại)	4
x				16 (tm)

Vậy để P nhận giá trị nguyên thì x = 16.

Bài 2:

a) $A = \sqrt {13 - 4\sqrt 3 } + \sqrt {13 + 4\sqrt 3 }$ $A = \sqrt {13 - 4\sqrt 3 } + \sqrt {13 + 4\sqrt 3 }$

$A = \sqrt {1 - 2.1.2\sqrt 3 + 12} + \sqrt {1 + 2.1.2\sqrt 3 + 12}$ $A = \sqrt {1 - 2.1.2\sqrt 3 + 12} + \sqrt {1 + 2.1.2\sqrt 3 + 12}$

$A = \sqrt {{{\left( {1 - 2\sqrt 3 } \right)}^2}} + \sqrt {{{\left( {1 + 2\sqrt 3 } \right)}^2}}$ $A = \sqrt {{{\left( {1 - 2\sqrt 3 } \right)}^2}} + \sqrt {{{\left( {1 + 2\sqrt 3 } \right)}^2}}$

$A = 2\sqrt 3 - 1 + 1 + 2\sqrt 3 = 4\sqrt 3$ $A = 2\sqrt 3 - 1 + 1 + 2\sqrt 3 = 4\sqrt 3$

b) $B = \frac{{2\sqrt 3 - 3\sqrt 2 }}{{\sqrt 6 }} + \frac{1}{{\sqrt 2 + \sqrt 3 }}$ $B = \frac{{2\sqrt 3 - 3\sqrt 2 }}{{\sqrt 6 }} + \frac{1}{{\sqrt 2 + \sqrt 3 }}$

$B = \frac{{\sqrt 6 \left( {\sqrt 2 - \sqrt 3 } \right)}}{{\sqrt 6 }} + \frac{1}{{\sqrt 2 + \sqrt 3 }}$ $B = \frac{{\sqrt 6 \left( {\sqrt 2 - \sqrt 3 } \right)}}{{\sqrt 6 }} + \frac{1}{{\sqrt 2 + \sqrt 3 }}$

$B = \sqrt 2 - \sqrt 3 + \frac{1}{{\sqrt 2 + \sqrt 3 }}$ $B = \sqrt 2 - \sqrt 3 + \frac{1}{{\sqrt 2 + \sqrt 3 }}$

$B = \frac{{\left( {\sqrt 2 - \sqrt 3 } \right)\left( {\sqrt 2 + \sqrt 3 } \right) + 1}}{{\sqrt 2 + \sqrt 3 }}$ $B = \frac{{\left( {\sqrt 2 - \sqrt 3 } \right)\left( {\sqrt 2 + \sqrt 3 } \right) + 1}}{{\sqrt 2 + \sqrt 3 }}$

$B = \frac{{\left( {2 - 3} \right) + 1}}{{\sqrt 2 + \sqrt 3 }} = \frac{{ - 1 + 1}}{{\sqrt 2 + \sqrt 3 }} = \frac{0}{{\sqrt 2 + \sqrt 3 }} = 0$ $B = \frac{{\left( {2 - 3} \right) + 1}}{{\sqrt 2 + \sqrt 3 }} = \frac{{ - 1 + 1}}{{\sqrt 2 + \sqrt 3 }} = \frac{0}{{\sqrt 2 + \sqrt 3 }} = 0$

Bài 3:

a) ${x^2} - 4x - 45 = 0$ ${x^2} - 4x - 45 = 0$

$\Leftrightarrow {x^2} - 9x + 5x - 45 = 0$ $\Leftrightarrow {x^2} - 9x + 5x - 45 = 0$

$\Leftrightarrow x\left( {x - 9} \right) + 5\left( {x - 9} \right) = 0$ $\Leftrightarrow x\left( {x - 9} \right) + 5\left( {x - 9} \right) = 0$

$\Leftrightarrow \left( {x + 5} \right)\left( {x - 9} \right) = 0 \Leftrightarrow \left[ \begin{array}{l} x + 5 = 0\\ x - 9 = 0 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = - 5\\ x = 9 \end{array} \right.$ $\Leftrightarrow \left( {x + 5} \right)\left( {x - 9} \right) = 0 \Leftrightarrow \left[ \begin{array}{l} x + 5 = 0\\ x - 9 = 0 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = - 5\\ x = 9 \end{array} \right.$

Vậy S = {-5; 9}

b) $\frac{{3\sqrt x + 1}}{{x - 9}} = \frac{2}{{\sqrt x - 3}} - \frac{{\sqrt x - 3}}{{\sqrt x + 3}}\left( {x \ge 0;x \ne 9} \right)$ $\frac{{3\sqrt x + 1}}{{x - 9}} = \frac{2}{{\sqrt x - 3}} - \frac{{\sqrt x - 3}}{{\sqrt x + 3}}\left( {x \ge 0;x \ne 9} \right)$

$\Leftrightarrow 3\sqrt x + 1 = 2\left( {\sqrt x + 3} \right) - \left( {\sqrt x - 3} \right)\left( {\sqrt x - 3} \right)$ $\Leftrightarrow 3\sqrt x + 1 = 2\left( {\sqrt x + 3} \right) - \left( {\sqrt x - 3} \right)\left( {\sqrt x - 3} \right)$

$\Leftrightarrow 3\sqrt x + 1 = 2\sqrt x + 6 - \left( {x - 6\sqrt x + 9} \right)$ $\Leftrightarrow 3\sqrt x + 1 = 2\sqrt x + 6 - \left( {x - 6\sqrt x + 9} \right)$

$\Leftrightarrow 3\sqrt x + 1 = 2\sqrt x + 6 - x + 6\sqrt x - 9$ $\Leftrightarrow 3\sqrt x + 1 = 2\sqrt x + 6 - x + 6\sqrt x - 9$

$\Leftrightarrow x - 5\sqrt x + 4 = 0$ $\Leftrightarrow x - 5\sqrt x + 4 = 0$

$\Leftrightarrow x - \sqrt x - 4\sqrt x + 4 = 0$ $\Leftrightarrow x - \sqrt x - 4\sqrt x + 4 = 0$

$\Leftrightarrow \sqrt x \left( {\sqrt x - 1} \right) - 4\left( {\sqrt x - 1} \right) = 0$ $\Leftrightarrow \sqrt x \left( {\sqrt x - 1} \right) - 4\left( {\sqrt x - 1} \right) = 0$

$\Leftrightarrow \left( {\sqrt x - 4} \right)\left( {\sqrt x - 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l} \sqrt x = 4\\ \sqrt x = 1 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = 16\\ x = 1 \end{array} \right.\left( {tm} \right)$ $\Leftrightarrow \left( {\sqrt x - 4} \right)\left( {\sqrt x - 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l} \sqrt x = 4\\ \sqrt x = 1 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = 16\\ x = 1 \end{array} \right.\left( {tm} \right)$

Vậy S = {1; 16}

Bài 4:

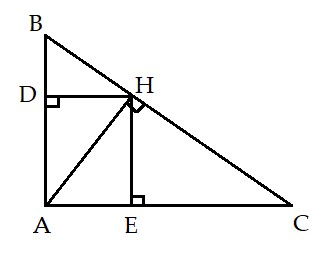
Đề thi giữa học kì 1 Toán 9 năm học 2020 - 2021 - Đề 1

a) + Xét tam giác ABC có: $\widehat A + \widehat B + \widehat C = {180^0}$ $\widehat A + \widehat B + \widehat C = {180^0}$(tổng ba góc trong tam giác)

mà $\widehat B + \widehat C = {90^0} \Rightarrow \widehat A = {90^0}$ $\widehat B + \widehat C = {90^0} \Rightarrow \widehat A = {90^0}$

+ Xét tứ giác ADHE có:

$\widehat {DAE} = {90^0}$ $\widehat {DAE} = {90^0}$(cmt)

$\widehat {HDA} = {90^0}$ $\widehat {HDA} = {90^0}$( $HD \bot AB$ $HD \bot AB$ - gt)

$\widehat {HEA} = {90^0}$ $\widehat {HEA} = {90^0}$( $HE \bot AC$ $HE \bot AC$ - gt)

$\Rightarrow$ $\Rightarrow$ADHE là hình chữ nhật (dhnb) (đpcm)

b) + Xét tam giác ABH có $\widehat {AHB} = {90^0};HD \bot AB$ $\widehat {AHB} = {90^0};HD \bot AB$:

$A{H^2} = AD.AB$ $A{H^2} = AD.AB$(hệ thức lượng trong tam giác vuông) (1)

+ Xét tam giác AHC có $\widehat {AHC} = {90^0};HE \bot AC$ $\widehat {AHC} = {90^0};HE \bot AC$:

$A{H^2} = AE.AC$ $A{H^2} = AE.AC$(hệ thức lượng trong tam giác vuông) (2)

+ Từ (1) và (2) $\Rightarrow AD.AB = AE.AC\left( { = A{H^2}} \right)$ $\Rightarrow AD.AB = AE.AC\left( { = A{H^2}} \right)$(đpcm)

c) + Xét tam giác ABC có $\widehat {BAC} = {90^0};AH \bot BC$ $\widehat {BAC} = {90^0};AH \bot BC$:

$A{B^2} + A{C^2} = B{C^2}$ $A{B^2} + A{C^2} = B{C^2}$(Pitago)

$\Rightarrow BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {100} = 10$ $\Rightarrow BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {100} = 10$(cm)

$\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}$ $\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}$(hệ thức lượng trong tam giác vuông)

$\Rightarrow AH = \sqrt {\frac{{A{B^2}.A{C^2}}}{{A{B^2} + A{C^2}}}} = \frac{{24}}{5}$ $\Rightarrow AH = \sqrt {\frac{{A{B^2}.A{C^2}}}{{A{B^2} + A{C^2}}}} = \frac{{24}}{5}$(cm)

+ Từ (1) $\Rightarrow AD = \frac{{A{H^2}}}{{AB}} = \frac{{96}}{{25}}$ $\Rightarrow AD = \frac{{A{H^2}}}{{AB}} = \frac{{96}}{{25}}$(cm)

+ Từ (2) $\Rightarrow AE = \frac{{A{H^2}}}{{AC}} = \frac{{72}}{{25}}$ $\Rightarrow AE = \frac{{A{H^2}}}{{AC}} = \frac{{72}}{{25}}$(cm)

---------------

Để chuẩn bị cho kì thi giữa kì 1 lớp 9 sắp tới, các em học sinh cần thực hành luyện đề để nắm được cấu trúc để thi cũng như làm quen với nhiều dạng đề khác nhau. VnDoc giới thiệu chuyên mục Đề thi giữa kì 1 lớp 9 với đầy đủ các môn, giúp các em ôn luyện trước kì thi, đồng thời cũng là tài liệu hay cho thầy cô tham khảo ra đề.

Chia sẻ, đánh giá bài viết

13

11.959

Bài trước

Bài sau