Bộ đề kiểm tra giữa học kì 1 môn Toán lớp 9

Mời các bạn tham khảo Bộ đề kiểm tra giữa học kì 1 môn Toán lớp 9 được VnDoc sưu tầm và đăng tải sau đây. Tài liệu bao gồm 10 đề thi Toán giữa kì 1 lớp 9 có đáp án đi kèm, sẽ là tài liệu hữu ích cho các em ôn tập, ôn luyện trước kì thi. Đây cũng là tài liệu hay giúp các em tập phân bổ thời gian làm bài hợp lý để đạt được điểm số cao cho kì thi giữa học kì 1 lớp 9. Dưới đây là nội dung chi tiết các em cùng tham khảo nhé.

Trong năm học 2025, chương trình Toán 9 tiếp tục có sự đổi mới với cấu trúc đề thi bám sát bộ sách giáo khoa mới và định hướng phát triển năng lực. Vì vậy, việc luyện tập với BỘ ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 TOÁN 9 (CẤU TRÚC MỚI) 2025 là cách hiệu quả giúp học sinh làm quen với dạng đề, nắm chắc kiến thức trọng tâm và rèn kỹ năng tư duy logic. Bộ đề được xây dựng khoa học, bám sát chuẩn kiến thức – kỹ năng, kèm đáp án chi tiết, giúp học sinh dễ dàng tự ôn tập, kiểm tra năng lực và chuẩn bị tốt cho kỳ thi giữa học kì.

Bên cạnh cấu trúc mới, nhiều trường vẫn tham khảo và áp dụng bộ đề thi ôn tập giữa học kì 1 dạng cũ có đáp án để học sinh có thêm lựa chọn luyện tập. Sự kết hợp giữa đề thi dạng mới và đề thi dạng cũ sẽ giúp học sinh không chỉ củng cố kiến thức toàn diện mà còn linh hoạt hơn trong việc xử lý nhiều dạng toán, từ cơ bản đến nâng cao. Đây chính là tài liệu hữu ích, phù hợp cho cả học sinh và giáo viên trong quá trình dạy và học.

Đề kiểm tra Toán 9 giữa học kì 1 số 1

Bài 1 (2,5 điểm). Cho biếu thức:
\(A = \left( \frac{1}{\sqrt{x} - 2} - \frac{1}{\sqrt{x} + 2} \right) \cdot \left( \frac{\sqrt{x} + 2}{2} \right)^{2}\)

a) Rút gọn biểu thức.

b) Tìm giá trị của x để \(A = \frac{3}{2}\).

Bài 2 (2 điểm). Thực hiện phép tính;

a) \(\sqrt{(\sqrt{8} - 4)^{2}} + \sqrt{8}\).                            b) \(\sqrt{9a} - \sqrt{144a} + \sqrt{49a}\ (\) với \(a > 0)\).

Bài 3 (2 điểm). Giải phương trình:

a) \(x - 6\sqrt{x} + 9 = 0\)                          b) \(\sqrt{x^{2} - 4} - 3\sqrt{x - 2} = 0\)

Bài 4 (3,5 điểm). Cho tam giác ABC có cạnh \(AB = 12\text{ }cm,AC = 16\text{ }cm,BC = 20\text{ }cm\). Kẻ đường cao AM. Kẻ ME vuông góc với AB.

a) Chứng minh tam giác ABC là tam giác vuông.

b) Tính độ dài \(AM,BM\).

c) Chứng minh \(AE \cdot AB = {AC}^{2} - {MC}^{2}\).

d) Chứng minh \(AE \cdot AB = MB \cdot MC = EM \cdot AC\).

-------------------------------Hết---------------------------------

Đáp án đề kiểm tra giữa học kì 1 môn Toán lớp 9 số 1

Bài	Hướng dẫn chấm	Thang điểm
1	a) \(A = \left( \frac{1}{\sqrt{x} - 2} - \frac{1}{\sqrt{x} + 2} \right)\left( \frac{\sqrt{x} + 2}{2} \right)^{2}\) \(= \frac{\sqrt{x} + 2 - \left( \sqrt{x} - 2 \right)}{\left( \sqrt{x} - 2 \right)\left( \sqrt{x} + 2 \right)}.\left( \frac{\sqrt{x} + 2}{2} \right)^{2}\) \(= \frac{4}{\left( \sqrt{x} - 2 \right)\left( \sqrt{x} + 2 \right)}.\left( \frac{\sqrt{x} + 2}{2} \right)^{2}\) \(= \frac{\sqrt{x} + 2}{\sqrt{x} - 2}\) b) \(\frac{\sqrt{x} + 2}{\sqrt{x} - 2} = \frac{3}{2} \Rightarrow 2(\sqrt{x} + 2) = 3(\sqrt{x} - 2)\)	0,5d
		0,5d
2 (2d)	a) \(\sqrt{(\sqrt{8} - 4)^{2}} + \sqrt{8} = |\sqrt{8} - 4| + \sqrt{8}\) \(= 4 - \sqrt{8} + \sqrt{8} = 4\)	0,5d
	b) \(\sqrt{9a} - \sqrt{144a} + \sqrt{49a} = 3\sqrt{a} - 12\sqrt{a} + 7\sqrt{a}\) \(= - 2\sqrt{a}\ (\ \text{với~}a > 0)\)	0,5d
3 (2d)	a) \(x - 6\sqrt{x} + 9 = 0\) \(\Leftrightarrow (\sqrt{x} - 3)^{2} = 0\) \(\Leftrightarrow \sqrt{x} - 3 = 0\) \(\Leftrightarrow x = 9\) ĐKXĐ: \(x \geq 0;\) Nhận định kết quả và trả lời	0,5d 0,25d 0,25d   0,25d
	b) \(\sqrt{x^{2} - 4} - 3\sqrt{x - 2} = 0\) \(\Leftrightarrow \sqrt{x - 2}\left( \sqrt{x + 2} - 3 \right) = 0\) \(\sqrt{x - 2} = 0\)  hoặc \(\sqrt{x + 2} - 3 = 0\) \(\Leftrightarrow x = 2;x = 7\) Điều kiện xác định\(x \leq - 2;x \geq 2\) . Nhận định kết quả và trả lời.	0,25d 0,25d 0,25d   0,25d
4	Vẽ hình a) Tam giác ABC là tam giác vuông (theo Pitago đảo). b) Ta có \(AM \cdot BC = AB \cdot AC\Rightarrow AM = 9,6(\text{ }cm)\) \({AB}^{2} = BM.BC \Rightarrow BM =7,2(\text{ }cm)\) c) \(AE.AB = {AM}^{2}{AM}^{2} = {AC}^{2} - {MC}^{2}\) . Kết luận ... d) \(AE \cdot AB = MB \cdot MC\left( = {AM}^{2} \right)\) Tam giác AEM đồng dạng với tam giác CMA \(\Rightarrow EM.AC = AM^{2}\) Vậy \(EM.AC = EA.AB = MB.MC\)	0,25d 0,75d 0,5d 0,5d 0,5d

Đề kiểm tra giữa học kì 1 môn Toán lớp 9 số 2

Bài 1 (1 điểm): Tìm điều kiện của x để các căn thức sau có nghĩa:

a, \(\sqrt{x - 2}\)                                     b) \(\sqrt{2 - 3x}\)

Bài 2 (2 điểm) Tính:

a) \(\sqrt{4.36}\)           b) \(\sqrt{\frac{25}{81} \cdot \frac{16}{49}}\)           c) \((\sqrt{8} - 3\sqrt{2}) \cdot \sqrt{2}\)                d) \(\frac{\sqrt{14} - \sqrt{7}}{1 - \sqrt{2}}\)

Bài 3 (1 điểm) Rút gọn biểu thức:

a) \(\sqrt{19 + \sqrt{136}} - \sqrt{19 - \sqrt{136}}\)                     b) \(\sqrt[3]{27} + \sqrt[3]{- 64} + 2 \cdot \sqrt[3]{125}\)

Bài 4 (1 điểm) Tìm x biết: \(\sqrt{4x + 20} - 2\sqrt{x + 5} + \sqrt{9x + 45} = 6\)

Bài 5 (2 điểm): Cho biểu thức:

\(A = \left( \frac{1}{x + 2\sqrt{x}} - \frac{1}{\sqrt{x} + 2} \right):\frac{1 - \sqrt{x}}{x + 4\sqrt{x} + 4}\ (\text{~với~}x > 0;x \neq 1)\)

a) Rút gon \(A\).

b) Tìm \(x\) để \(F = \frac{5}{2}\).

Bài 6 (3 điểm): Cho tam giác ABC vuông tai A có đường cao AH chia cạnh huyền BC thành hai đoạn: \(BH = 4\text{ }cm\) và \(HC = 6\text{ }cm\).

a) Tính dộ dài các doan \(AH,AB,AC\).

b) Gọi M là trung điểm của AC. Tính số đo góc AMB (làm tròn đến độ).

c) Kẻ AK vuông góc với \(BM;(K \in BM)\).Chứng minh: \(\bigtriangleup BKC \sim \bigtriangleup BHM\).

Đáp án đề kiểm tra giữa học kì 1 môn Toán lớp 9 số 2

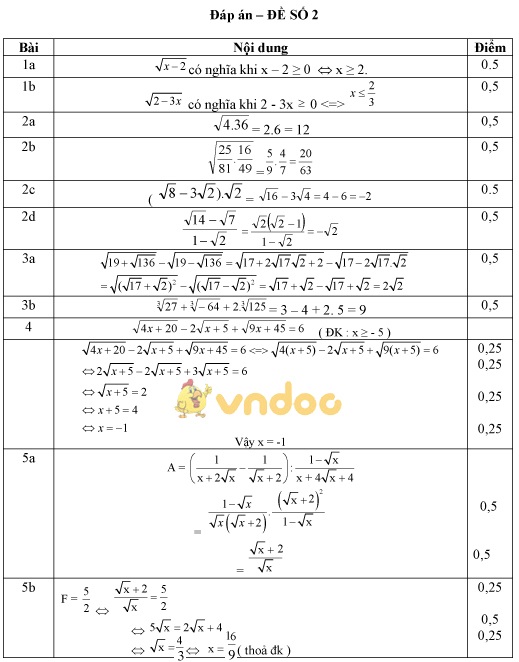
Đề kiểm tra giữa học kì 1 môn Toán lớp 9 số 3

Câu 1: (2,0 điểm).

a. Thực hiện phép tính: \(\sqrt{27}:\sqrt{3} - \sqrt{48} + 2\sqrt{12}\)

b. Với giá trị nào của m thi hàm số \(y = (m - 1)x + 3\) đồng biến.

Câu 2: (2,0 điểm). Cho \(A = \frac{\sqrt{x}}{\sqrt{x} - 5} - \frac{10\sqrt{x}}{x - 25} - \frac{5}{\sqrt{x} + 5}\)

a. Rút gon A.

b. Tìm các giá trị của x để A > 0.

Câu 3: ( \(\mathbf{2,0}\) điểm). Giải các phương trình và hệ phương trình sau:

a. \(\sqrt{(x - 1)^{2}} = 4\)                                        b. \(\left\{ \begin{matrix} 2x - y = 5 \\ x + y = 1 \end{matrix} \right.\)

Câu 4: (3,0 điểm). Cho dường tròn tâm O bán kính R và một diểm M nằm ngoài đường tròn. Qua M kẻ tiếp tuyến MA với đường tròn (A là tiếp điểm). Tia Mx nằm giữa MA và MO cắt đường tròn \((O;R)\) tại hai điểm C và \(D\ (C\) nằm giữa M và D\()\). Gọi I là trung điểm của dây CD, kẻ AH vuông góc với MO tại H.

a. Tinh OH. OM theo R.

b. Chứng minh: Bốn điểm \(M,A,I,O\) cùng thuộc một đường tròn.

c. Gọi K là giao điểm của OI với HA. Chứng minh KC là tiếp tuyến của dường tròn (\(O;R\)).

Câu 5: (1,0 điểm). Cho \(x > 0\). Tìm giá trị nhỏ nhất của biểu thức:

\(A = x^{2} - 3x + \frac{4}{x} + 2016\)

Đáp án đề kiểm tra giữa học kì 1 môn Toán lớp 9 số 3

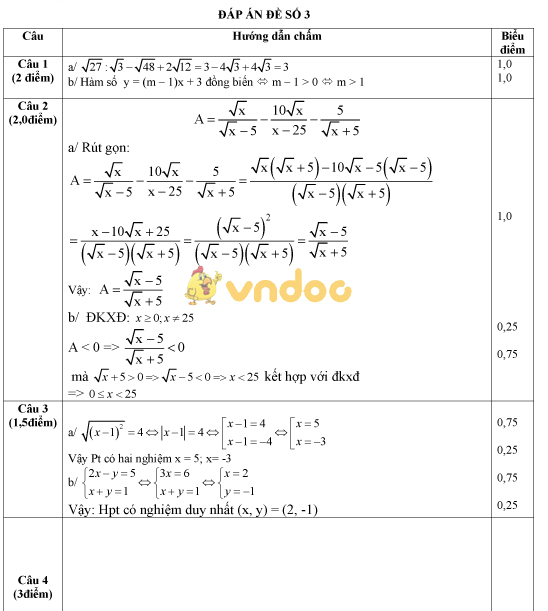
Đề kiểm tra giữa học kì 1 môn Toán lớp 9 số 4

Đáp án đề kiểm tra giữa học kì 1 môn Toán lớp 9 số 4

Tài liệu vẫn còn, mời các bạn tải về để tham khảo trọn bộ

------------------------------------------------------------------

Để chuẩn bị cho kì thi giữa học kì 1 lớp 9 sắp tới, các em học sinh cần ôn tập theo đề cương, bên cạnh đó cần thực hành luyện đề để làm quen với nhiều dạng đề khác nhau cũng như nắm được cấu trúc đề thi. Chuyên mục Đề thi giữa học kì 1 lớp 9 trên VnDoc tổng hợp đề thi của tất cả các môn, là tài liệu phong phú và hữu ích cho các em ôn tập và luyện đề. Đây cũng là tài liệu hay cho thầy cô tham khảo ra đề. Mời thầy cô và các em tham khảo.