Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 8 Khóa học Lớp 8 Toán 8 - Cánh diều
Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ 79.000đ

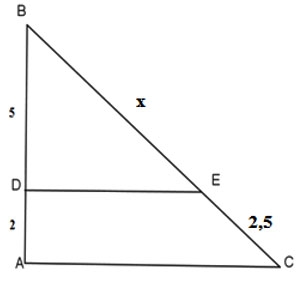
Luyện tập Định lí Thalès trong tam giác Cánh Diều

Bài tập Toán 8 Cánh diều

Vndoc.com xin gửi tới bạn đọc bài Luyện tập về Định lí Thalès trong tam giác lớp 8 sách Kết nối tri thức. Các câu hỏi được biên soạn bám sát chương trình, phù hợp cho ôn tập, kiểm tra và rèn luyện kỹ năng làm bài trắc nghiệm.

👇Mời bạn làm bài tập online dưới đây nhé!

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 20 câu
  • Điểm số bài kiểm tra: 20 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu!!
00:00:00
  • Câu 1: Thông hiểu
    Tính giá trị biểu thức

    Cho hình bên, biết DE // AC

    Định lí Thales

    Tính giá trị của x - 1

    Hướng dẫn:

    Theo bài ra ta có: DE // AC, áp dụng định lí Thales ta có:

    \begin{matrix} \dfrac{{BE}}{{BC}} = \dfrac{{BD}}{{BA}} \Leftrightarrow \dfrac{x}{{x + 2,5}} = \dfrac{5}{{5 + 2}} \hfill \\ \Leftrightarrow \dfrac{x}{{x + 2,5}} = \dfrac{5}{7} \Leftrightarrow 7x = 5x + 12,5 \hfill \\ \Leftrightarrow x = 6,25 \hfill \\ \end{matrix}

    Vậy x - 1 = 5,25

  • Câu 2: Thông hiểu
    Tính độ dài AD

    Trong tam giác ABC kẻ đường thẳng song song với BC cắt các cạnh AB và AC theo thứ tự tại D và E. Qua E kẻ đường thẳng song song với CD, cắt AB ở F. Tính độ dài AD, biết AB = 16, AF = 9.

    Hướng dẫn:

    Hình vẽ minh họa 

    Định lí Thales

    Với EF // CD, áp dụng định lý Thales ta có:

    \frac{{AF}}{{AD}} = \frac{{AE}}{{AC}}

    Với DE // BC, áp dụng định lý Thales ta có:

    \frac{{AE}}{{AC}} = \frac{{AD}}{{AB}}

    \begin{matrix} \Rightarrow \dfrac{{AF}}{{AD}} = \dfrac{{AD}}{{AB}} \Rightarrow A{D^2} = AF.AB \hfill \\ \Rightarrow A{D^2} = 9.16 \Rightarrow A{D^2} = 144 \Rightarrow AD = 12 \hfill \\ \end{matrix}

  • Câu 3: Nhận biết
    Chọn câu trả lời đúng

    Tình giá trị của x trong hình vẽ, biết ED ⊥ AB, AC ⊥ AB

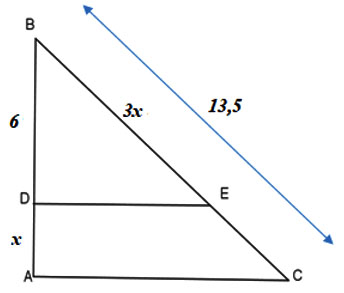
    Định lí Thales

    Hướng dẫn:

    Ta có: ED ⊥ AB, AC ⊥ AB

    ⇒ DE // AC (từ vuông góc đến song song)

    Áp dụng định lý Thales, ta có:

    \begin{matrix} \dfrac{{BD}}{{DA}} = \dfrac{{BE}}{{EC}} \Rightarrow \dfrac{6}{x} = \dfrac{{3x}}{{13,5 - 3x}} \hfill \\ \Rightarrow 6.\left( {13,5 - 3x} ight) = 3{x^2} \hfill \\ \Rightarrow {x^2} + 6x - 27 = 0 \hfill \\ \Rightarrow {x^2} - 3x + 9x - 27 = 0 \hfill \\ \Rightarrow x\left( {x - 3} ight) + 9\left( {x - 3} ight) = 0 \hfill \\ \Rightarrow \left( {x + 9} ight)\left( {x - 3} ight) = 0 \hfill \\ \Rightarrow \left[ {\begin{array}{*{20}{c}} {x + 9 = 0} \\ {x - 3 = 0} \end{array}} ight. \Rightarrow \left[ {\begin{array}{*{20}{c}} {x = - 9} \\ {x = 3} \end{array}} ight. \hfill \\ \end{matrix}

    Vậy x = 3 thỏa mãn.

  • Câu 4: Thông hiểu
    Chọn đáp án đúng

    Quan sát hình vẽ sau:

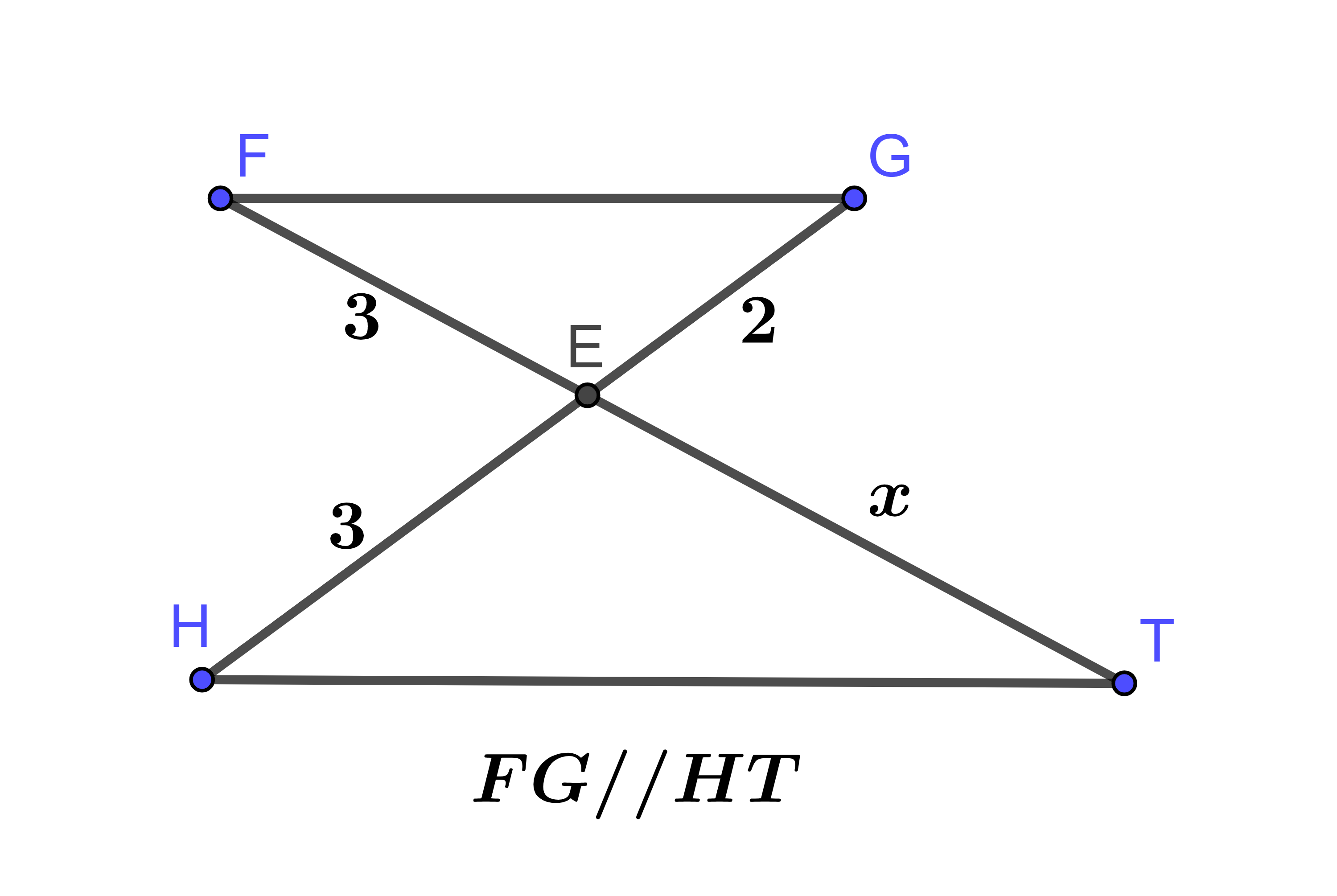
    Định lí Thales

    Giá trị của x là: 

    Hướng dẫn:

    Áp dụng hệ quả của định lí Thales với FG//HT ta có:

    \frac{{EF}}{{ET}} = \frac{{EG}}{{HE}} \Rightarrow ET = \frac{{EF.HE}}{{EG}} = \frac{{3.3}}{2} = 4,5

  • Câu 5: Thông hiểu
    Chọn câu trả lời đúng

    Xác định giá trị của x trong hình vẽ, biết DE // AC

    Định lí Thales

    Hướng dẫn:

    Theo bài ra ta có:  DE // AC, áp dụng định lí Thales ta có:

    \begin{matrix} \dfrac{{BE}}{{BC}} = \dfrac{{BD}}{{BA}} \Leftrightarrow \dfrac{x}{{x + 2,5}} = \dfrac{5}{{5 + 2}} \hfill \\ \Leftrightarrow \dfrac{x}{{x + 2,5}} = \dfrac{5}{7} \Leftrightarrow 7x = 5x + 12,5 \hfill \\ \Leftrightarrow x = 6,25 \hfill \\ \end{matrix}

  • Câu 6: Nhận biết
    Tính độ dài AB

    Cho hình vẽ:

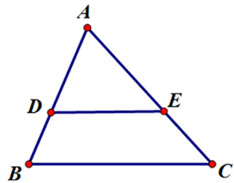
    Định lí Thales

    Trong đó DE // BC, AE = 12, DB = 18, CA = 36. Độ dài AB bằng:

    Hướng dẫn:

    Ta có: DE // BC, theo định lý Thales ta có:

    \begin{matrix} \dfrac{{AE}}{{EC}} = \dfrac{{AD}}{{DB}} \Leftrightarrow \dfrac{{12}}{{36 - 12}} = \dfrac{{AD}}{{18}} \hfill \\ \Leftrightarrow \dfrac{{12}}{{24}} = \dfrac{{AD}}{{18}} \Leftrightarrow AD = \dfrac{{18.12}}{{24}} = 9\left( {cm} ight) \hfill \\ \Rightarrow AB = AD + DB = 9 + 18 = 27\left( {cm} ight) \hfill \\ \end{matrix}

  • Câu 7: Vận dụng
    Tính độ dài cạnh IK

    Cho hình bình hành ABCD. Lấy điểm F là trung điểm của BC, điểm E thuộc cạnh AB sao cho AE = \frac{1}{2}BE. Gọi giao điểm của AC với các đường thẳng DE và DF lần lượt là I, K. Tính độ dài cạnh IK, biết độ dài cạnh AC là 24 cm.

     

    Hướng dẫn:

    Hình vẽ minh họa

    Ta có: AE = \frac{1}{2}BE \Rightarrow \frac{AE}{AB} = \frac{1}{3}

    Ta có: AB // CD

    \Rightarrow \frac{AI}{IC} = \frac{AE}{CD} = \frac{AE}{AB} = \frac{1}{3} (Theo định lí Thales)

    Do đó: AI = \frac{1}{4}AC = \frac{1}{4}.24 = 6(cm)

    Ta lại có: AD // BC

    \Rightarrow \frac{CK}{AK} = \frac{CF}{AD} = \frac{CF}{BC} = \frac{1}{2}

    Do đó: CK = \frac{1}{3}AC = \frac{1}{3}.24 = 8(cm)

    \Rightarrow IK = 24 - 6 - 8 = 10(cm)

  • Câu 8: Thông hiểu
    Tính giá trị của biểu thức

    Cho hình vẽ:

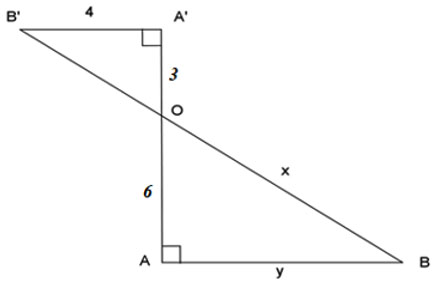
    Định lí Thales

    Giá trị biểu thức x - y là:

    Hướng dẫn:

    Áp dụng định lý Pythagore cho tam giác vuông OA’B’, ta có:

    OA’^2 + A’B’^2 = OB’^2

    ⇔ 3^2 + 4^2 = OB’^2

    ⇔ OB’^2 = 25 ⇒ OB’ = 5

    Lại có:

    A’B’ ⊥ AA’, AB ⊥ AA’ ⇒ A’B’// AB

    (Theo định lý từ vuông góc đến song song)

    Áp dụng định lý Thales, ta có:

    \begin{matrix} \dfrac{{OA'}}{{OA}} = \dfrac{{OB'}}{{OB}} = \dfrac{{A'B'}}{{AB}} \Rightarrow \dfrac{3}{6} = \dfrac{5}{x} = \dfrac{4}{y} \hfill \\ \Rightarrow \left\{ {\begin{array}{*{20}{c}} {x = \dfrac{{5.6}}{3} = 10} \\ {y = \dfrac{{4.6}}{3} = 8} \end{array}} ight. \hfill \\ \end{matrix}

    Vậy x-y=2

  • Câu 9: Thông hiểu
    Tính độ dài BF

    Cho hình thang ABCD; (AB // CD) có BC = 15cm. Điểm E thuộc cạnh AD sao cho \frac{AE}{AD} = \frac{1}{3} Qua E kẻ đường thẳng song song với CD, cắt BC ở F. Tính độ dài BF.

    Hướng dẫn:

    Hình vẽ minh họa

    Định lí Thales

    Gọi I là giao điểm của AC và EF.

    Xét tam giác ACB có IF // AB nên theo định lý Thales ta có:

    \begin{matrix} \dfrac{{BF}}{{BC}} = \dfrac{{AI}}{{AC}} = \dfrac{{AE}}{{AD}} = \dfrac{1}{3} \hfill \\ \Rightarrow BF = \dfrac{1}{3}BC = \dfrac{1}{3}.15 = 5\left( {cm} ight) \hfill \\ \end{matrix}

  • Câu 10: Thông hiểu
    Tìm x

    Tìm giá trị của x trên hình vẽ.

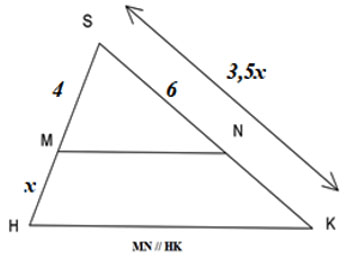
    Định lí Thales

    Hướng dẫn:

    Ta có: MN//HK, áp dụng định lí Thales ta có:

    \begin{matrix} \dfrac{{SM}}{{SH}} = \dfrac{{SN}}{{SK}} \Rightarrow \dfrac{{SM}}{{SM + MH}} = \dfrac{{SN}}{{SK}} \hfill \\ \Rightarrow \dfrac{4}{{x + 4}} = \dfrac{6}{{3,5x}} \hfill \\ \Rightarrow 4.3,5x = 6.\left( {x + 4} ight) \hfill \\ \Rightarrow 14x = 6x + 24 \hfill \\ \Rightarrow 8x = 24 \hfill \\ \Rightarrow x = 3 \hfill \\ \end{matrix}

  • Câu 11: Nhận biết
    Chọn khẳng định đúng

    Cho tam giác ABC, AB < AC như hình vẽ:

    Định lí Thales

    Chọn khẳng định đúng.

     

    Hướng dẫn:

    Theo định lý đảo của định lý Thales:

    Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.

  • Câu 12: Thông hiểu
    Điền đáp án vào chỗ trống

    Cho tam giác ABC có AB = 8cm. Lần lượt lấy trên cạnh AB, AC các điểm B' và C' sao cho B'C' // BC và AB' = 2cm, AC' = 3cm. Khi đó độ dài cạnh AC là: 12cm

    Đáp án là:

    Cho tam giác ABC có AB = 8cm. Lần lượt lấy trên cạnh AB, AC các điểm B' và C' sao cho B'C' // BC và AB' = 2cm, AC' = 3cm. Khi đó độ dài cạnh AC là: 12cm

    Hình vẽ minh họa

    Định lí Thales

    Ta có: B'C'//BC; B' ∈ AB, C' ∈ AC

    Áp dụng hệ quả của định lí Thales  ta có:

    \Rightarrow \frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} = \frac{{B'C'}}{{BC}}

    \Rightarrow \frac{2}{8} = \frac{3}{{AC}} \Rightarrow AC = \frac{{3.8}}{2} = 12(cm)

  • Câu 13: Thông hiểu
    Tính độ dài AF

    Cho tam giác ABC có AB = 9cm, lấy điểm D thuộc cạnh AB sao cho AD = 6cm. Kẻ DE song song với BC (E thuộc AC), kẻ EF song song với CD (F thuộc AB). Tính độ dài AF.

    Hướng dẫn:

    Hình vẽ minh họa

    Định lí Thales

    Với EF // CD, áp dụng định lý Thales ta có:

    \frac{{AF}}{{AD}} = \frac{{AE}}{{AC}}

    Với DE // BC, áp dụng định lý Thales ta có:

    \frac{{AE}}{{AC}} = \frac{{AD}}{{AB}}

    \Rightarrow \frac{{AF}}{{AD}} = \frac{{AD}}{{AB}} \Rightarrow \frac{{AF}}{6} = \frac{6}{9} \Rightarrow AF = \frac{{6.6}}{9} = 4\left( {cm} ight)

  • Câu 14: Thông hiểu
    Tính tỉ số hai cạnh

    Cho hình thang ABCD; ( AB//CD ) có O là giao điểm của hai đường chéo. Đường thẳng qua O song song hai đáy và cắt AD, BC lần lượt tại E và F. Tính tỉ số \frac{{OE}}{{OF}}.

    Hướng dẫn:

    Hình vẽ minh họa

     

    Định lí Thales

    Áp dụng hệ quả của định lí Thales cho OE//DC, OF//DC và AB//DC ta được:

    \left\{ \begin{gathered} \dfrac{{OE}}{{DC}} = \dfrac{{AO}}{{AC}} \hfill \\ \dfrac{{OF}}{{DC}} = \dfrac{{BO}}{{DB}} \hfill \\ \dfrac{{AO}}{{AC}} = \dfrac{{BO}}{{BD}} \hfill \\ \end{gathered} ight. \Rightarrow \dfrac{{EO}}{{DC}} = \dfrac{{OF}}{{DC}} \Rightarrow OE = OF

    Vậy \frac{{OE}}{{OF}} =1

  • Câu 15: Vận dụng
    Cho hình vẽ:

    Khẳng định nào sau đây đúng?

  • Câu 16: Vận dụng
    Cho tam giác ABC có cạnh BC = 12 cm. Trên cạnh AB lấy điểm D và E sao cho AD = DE = EB. Từ D, E kẻ các đường thẳng song song với BC cắt AC theo thứ tự tại M, N. Khi đó, độ dài đoạn thẳng DM và EN là:
  • Câu 17: Thông hiểu
    Tìm y

    Tình giá trị y trong hình vẽ sau:

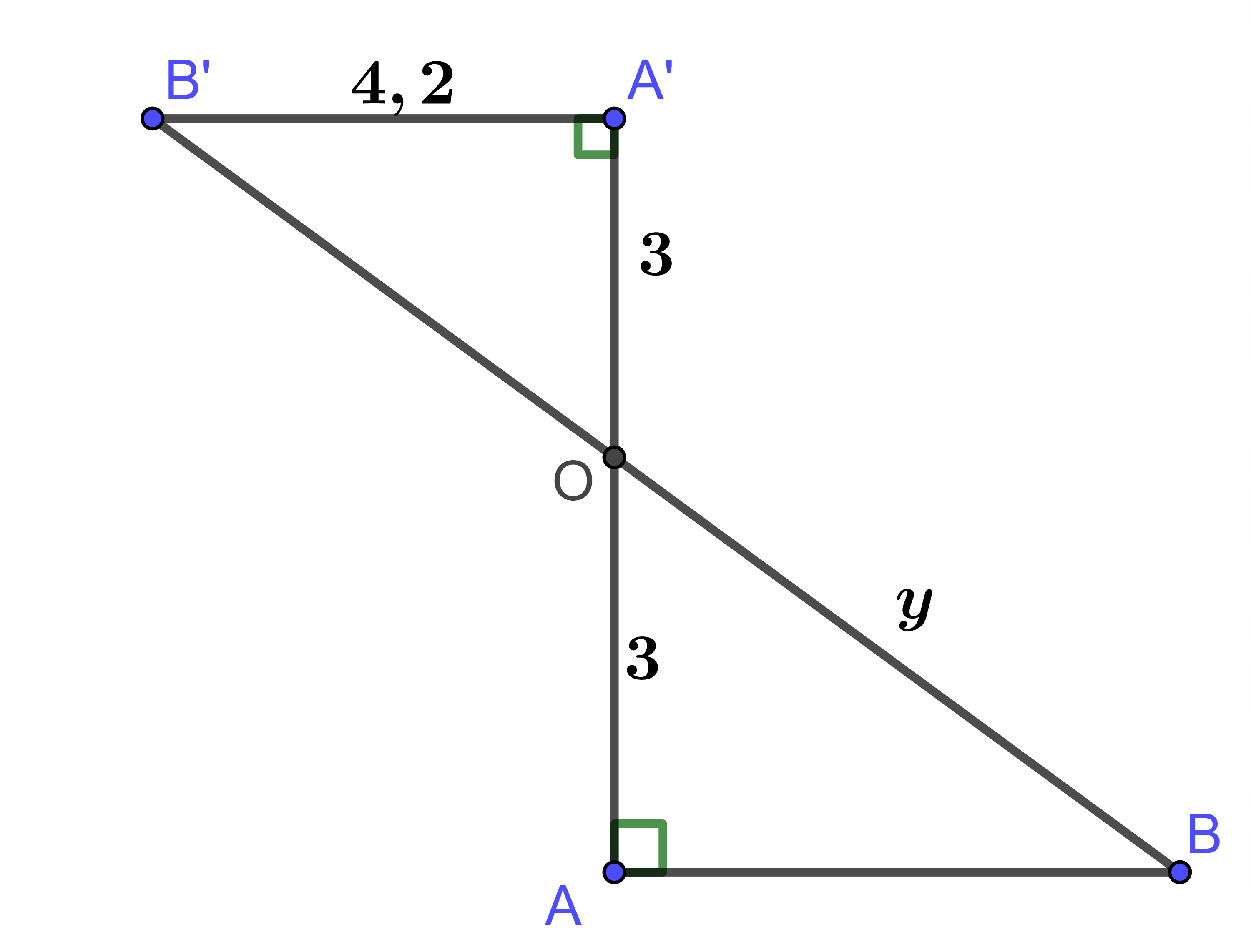
    Định lí Thales

    Hướng dẫn:

    Ta có: A'B'//AB vì cùng vuông góc AA'

    Áp dụng hệ quả của định lí Thales ta có:

    \frac{{AB}}{{A'B'}} = \frac{{AO}}{{A'O}} \Rightarrow \frac{x}{{4,2}} = \frac{6}{3} \Rightarrow x = 8,4

    Áp dụng định lí Pythagore trong tam giác OAB ta có:

    OB^2 = AB^2 + OA^2

    \Rightarrow y = \sqrt {8,{4^2} + {6^2}} \approx 10,32

  • Câu 18: Vận dụng
    Tính diện tích tam giác

    Cho hình thang ABCD; (AB // CD), O là giao điểm của hai đường chéo. Tính diện tích tam giác COD, biết hình thang có diện tích 36cm^2, AB = 4cm, CD = 8cm.

    Hướng dẫn:

    Hình vẽ minh họa

    Định lí Thales

    Kẻ AH ⊥ DC; OK ⊥ DC tại H, K => AH // OK

    Chiều cao của hình thang: AH = \frac{{2S}}{{AB + CD}} = \frac{{2.36}}{{4 + 8}} = 6\left( {cm} ight)

    Vì AB // CD (do ABCD là hình thang) nên theo định lý Thales ta có

    \begin{matrix} \dfrac{{OC}}{{OA}} = \dfrac{{CD}}{{AB}} = \dfrac{8}{4} = 2 \hfill \\ \Rightarrow \dfrac{{OC}}{{OA + OC}} = \dfrac{2}{{2 + 1}} \hfill \\ \Rightarrow \dfrac{{OC}}{{AC}} = \dfrac{2}{3} \hfill \\ \end{matrix}

    Vì AH // OK (chứng minh trên) nên theo định lý Thales cho tam giác AHC ta có:

    \begin{matrix} \dfrac{{OK}}{{AH}} = \dfrac{{OC}}{{AC}} = \dfrac{2}{3} \Rightarrow OK = \dfrac{2}{3}AH \hfill \\ \Rightarrow OK = \dfrac{2}{3}.6 = 4\left( {cm} ight) \hfill \\ \end{matrix}

    Vậy diện tích tam giác OCD là: {S_{COD}} = \frac{1}{2}.OK.DC = \frac{1}{2}.4.8 = 16c{m^2}

  • Câu 19: Thông hiểu
    Tính giá trị x

    Cho hình vẽ và tìm giá trị x

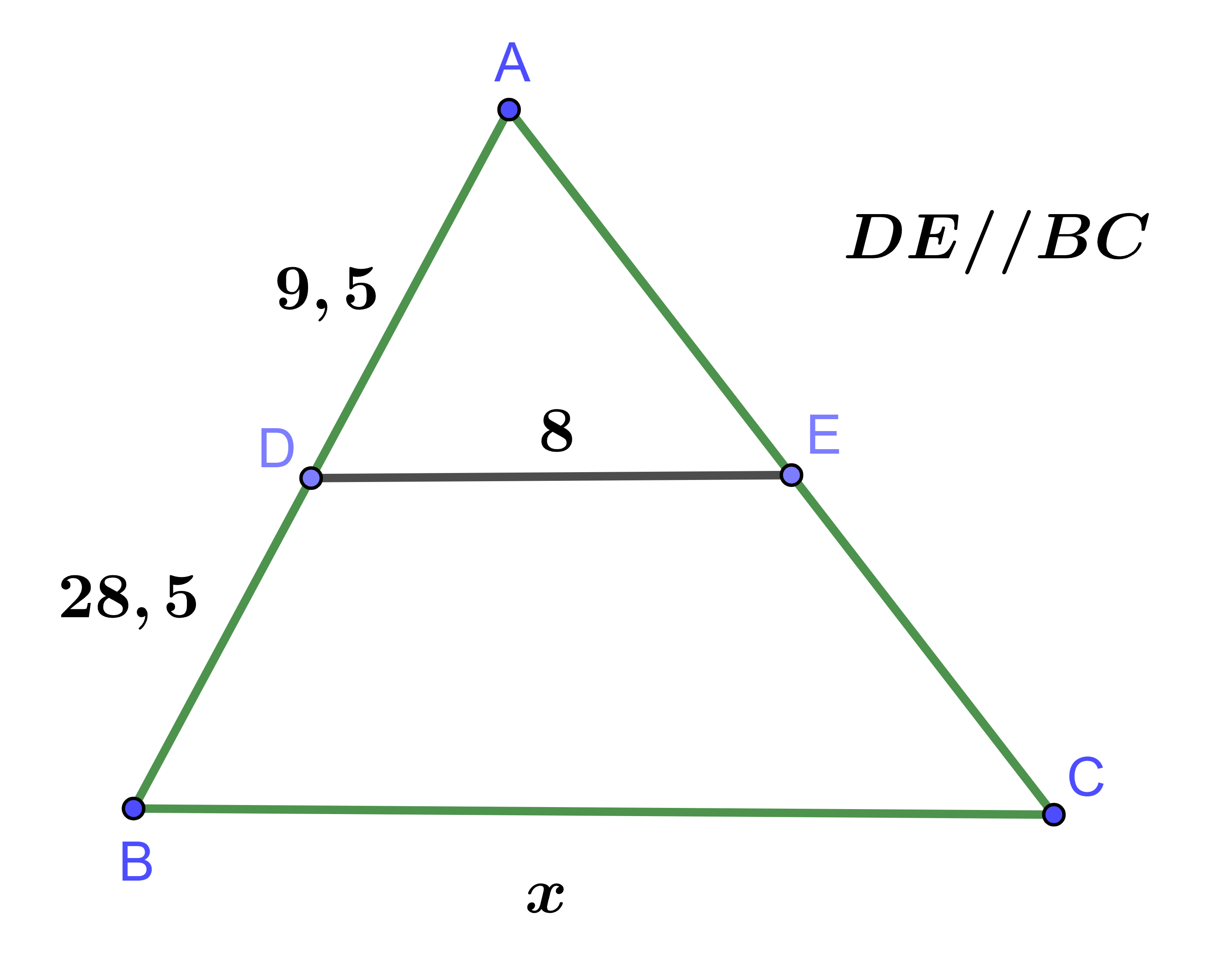
    Định lí Thales

    Hướng dẫn:

    Ta có: DE//BC

    Áp dụng hệ quả của định lí Thales ta có:

    \begin{matrix} \frac{{AD}}{{AB}} = \dfrac{{DE}}{{BC}} \Leftrightarrow \dfrac{{9,5}}{{9,5 + 28,5}} = \dfrac{8}{x} \hfill \\ \Rightarrow x = \dfrac{{\left( {9,5 + 28,5} ight).8}}{{9,5}} = 32 \hfill \\ \end{matrix}

  • Câu 20: Vận dụng
    Điền đáp án đúng vào chỗ trống

    Cho tam giác ABC có diện tích là 90 cm2, kẻ AH vuông góc với BC. Trên cạnh AH lấy các điểm K và I sao cho AK = KI = HI. Từ điểm I, K lần lượt kẻ các đường thẳng EF // BC, MN // BC với E, M ∈ AB, F, N ∈ AC. Khi đó diện tích tứ giác MNEF bằng bao nhiêu?

    Kết quả: 30 cm2.

     

    Đáp án là:

    Cho tam giác ABC có diện tích là 90 cm2, kẻ AH vuông góc với BC. Trên cạnh AH lấy các điểm K và I sao cho AK = KI = HI. Từ điểm I, K lần lượt kẻ các đường thẳng EF // BC, MN // BC với E, M ∈ AB, F, N ∈ AC. Khi đó diện tích tứ giác MNEF bằng bao nhiêu?

    Kết quả: 30 cm2.

     

    Hình vẽ minh họa

    Định lí Thales

    Ta có:

    \begin{matrix} NK//CH \Rightarrow \dfrac{{AK}}{{AH}} = \dfrac{{AN}}{{AC}} \Rightarrow \dfrac{{AN}}{{AC}} = \dfrac{1}{3} \hfill \\ MN//BC \Rightarrow \dfrac{{MN}}{{BC}} = \dfrac{{AN}}{{AC}} \Rightarrow \dfrac{{MN}}{{BC}} = \dfrac{1}{3} \hfill \\ IF//CH \Rightarrow \dfrac{{AI}}{{AH}} = \dfrac{{AF}}{{AC}} \Rightarrow \dfrac{{AF}}{{AC}} = \dfrac{2}{3} \hfill \\ EF//BC \Rightarrow \dfrac{{EF}}{{BC}} = \dfrac{{AF}}{{AC}} \Rightarrow \dfrac{{EF}}{{BC}} = \dfrac{2}{3} \hfill \\ \end{matrix}

    Xét tứ giác MNFE có MN // FE và KI ⊥ MN.

    Do đó MNFE là hình thang có 2 đáy MN, FE, chiều cao KI.

    \Rightarrow {S_{MNEF}} = \frac{1}{2}\left( {MN + EF} ight).KI

    \Rightarrow {S_{MNEF}} = \frac{1}{2}\left( {\frac{1}{3}BC + \frac{2}{3}BC} ight).\frac{1}{3}AH = \frac{1}{3}{S_{ABC}} = 30\left( {c{m^2}} ight)

0/20
20 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (15%):
    2/3
  • Thông hiểu (60%):
    2/3
  • Vận dụng (25%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
  • Điểm thưởng: 0
Làm lại
Bạn còn 1 lượt làm bài tập miễn phí. Hãy mua tài khoản VnDoc PRO để học không giới hạn nhé! Bạn đã HẾT lượt làm bài tập miễn phí! Hãy mua tài khoản VnDoc PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé! Mua ngay
1
106 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Tìm bài trong mục này
🖼️

Toán 8 - Cánh diều
Xem thêm