Phương pháp giải bài Toán với chiếc cân 2 đĩa
Phương pháp giải bài toán với CHIẾC CÂN 2 ĐĨA
Phương pháp giải bài Toán với chiếc cân 2 đĩa bao gồm ví dụ minh họa kèm theo đáp án chi tiết cho từng ví dụ và các dạng bài tập giúp các em học sinh ôn tập, cách giải các dạng Toán này cho các kỳ thi học sinh giỏi tốt nhất. Mời các em cùng tham khảo.
1. Hiểu thế nào về dạng toán cân bi cân vàng ở tiểu học:
Trong một số đề thi học sinh giỏi bậc tiểu học, thi tin học chúng ta thường bắt gặp những bài toán yêu cầu dùng cân phát hiện 1 trong số "viên bi", "bóng", "nhẫn"... không đủ trọng lượng nằm trong tổng thể n "sản phẩm". Đó không phải là toán "mẹo", mà phải dùng thuật toán và suy luận để sao cho chỉ cần tối thiểu m lần cân, đủ để phát hiện. Các đề đó cũng chưa nằm trong kiến thức xác suất, mà chỉ trong các phép cộng trừ nhân chia đơn giản.
2. Một số bài mẫu với chiếc cân 2 đĩa
Bài số 1:
Có 8 quả bóng hoàn toàn giống nhau về hình thể, màu sắc, kích thước; nhưng 1 quả nhẹ cân không đảm bảo cho cuộc thi đấu quan trọng. Làm sao chỉ 2 lần cân đã phát hiện, loại bỏ quả bóng đó?
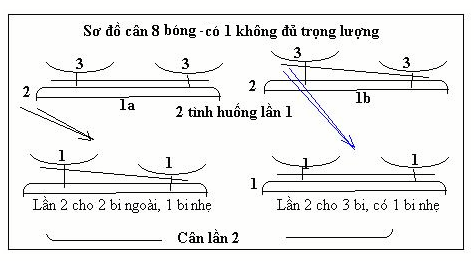
Bài giải:
* Nếu không khống chế số lần cân thì cứ chia đôi 8/2 =4, rồi 4/2 = 2 và 2/2 = 1 lần lượt sẽ ra, nhưng phải 3 lần cân.
* Dùng thuật toán "chia ba" như sau: 8 quả bóng chia làm 3 phần (2 phần đặt lên 2 đĩa cân, mỗi phần 3 quả, phần còn lại 2 quả để ngoài).
- Tình huống 1a: 2 đĩa cân thăng bằng, nghĩa là quả thiếu cân nằm trong 2 quả để ngoài. Vậy chỉ việc cân 2 quả ngoài đã phát hiện quả thiếu cân.
- Tình huống 1b: Một đĩa 3 quả nhẹ cân thì đem 3 quả này chia 3, 1 quả đặt ngoài, 2 quả kia lên đĩa cân. Chắc chắn sẽ phát hiện quả thiếu cân.
Vậy tình huống nào cũng chỉ cần cân 2 lần (Đáp án 2 lần)
Bài số 2:
"Có 80 cái nhẫn trong đó 1 cái nhẹ hơn 79 cái kia. Làm sao chỉ cân 4 lần mà lấy được chiếc nhẫn nhẹ hơn khỏi 79 chiếc kia".
Bài giải:
Cân theo sơ đồ sau:
* Lần I Mỗi đĩa 27 cái (27 x2 = 54; cái còn để ngoài 26 *).
Nếu 2 đĩa thăng bằng thì cân số 26 để ngoài theo sơ đồ *****. Nếu 1 đĩa 27 cái nhẹ hơn thì cân lần II
** Lần II: Mỗi đĩa 9 cái; để ngoài 9 cái.
Nếu phát hiện một trong số lô 9 cái nhẹ thì cân lần III.
*** Lần III: Mỗi đĩa cân đặt 3 cái, để ngoài 3 cái.
Nếu phát hiện một trong số lô 3 cái nhẹ thi cân lần IV.
**** Lần IV: Dễ dàng phát hiên đúng cái nhẹ hơn khi đặt mỗi cái / 1 đĩa.
***** Lần II (cho trường hợp rơi vào 26 cái để ngoài lần I)
Đặt mỗi đĩa 9 cái; 8 để ngoài. Nếu phát hiện lô 9 cái thì cân tiếp theo sơ đồ ***.
Nếu rơi vào lô 8 ngoài thì cân lần III
****** Lần III (cho lô 8 cái): Đặt mỗi đĩa 3 cái, để ngoài 2.
Nếu rơi vào lô 3 cái thì cân tiếp theo sơ đồ ****(lần IV).
Còn nếu phát hiện lô 2 cái thì cân lần IV.
Đến đây thì quá dễ để tìm cái nhẫn thiếu cân. (xem sơ đồ minh họa)
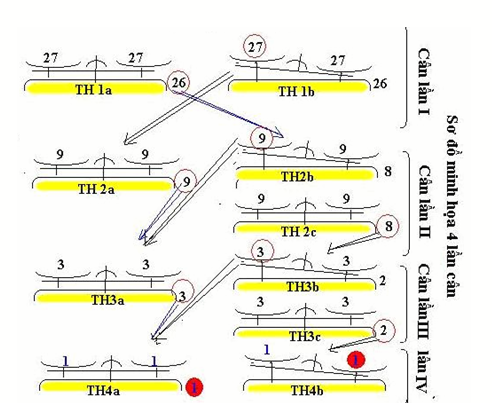
Vậy tình huống nào cũng chỉ cần cân 4 lần (đúng Đáp án)
3. Một vài bàn luận với dạng toán này - Đưa ra phương pháp chung:
* Cả 2 bài mẫu trên các lần cân đều chia ba tổng số "sản phẩm" để cuối cùng chỉ còn 2 mới chia đôi (tất nhiên vì hết cách chia ba). Cũng vì thế gọi thuật toán này là "thuật toán chia ba".
* Dựa theo thuật toán này người ta có thể thay đổi dữ kiện n (số sản phẩm) và m (số lần cân cho phép) để ra đề với n > m, trong đó m phụ thuộc n như sau:

Thường đề ít khi cho n là một số chia hết cho 3 mà hay cho số chẵn, xấp xỉ; thí dụ đáng lẽ cho n = 9, 27, 81... thì lấy n = 8, 24 , 80... Để đánh bẫy người cứ quen chia đôi.
* Sơ đồ trên, số m là số lần cân ít nhất tương ứng với n sản phẩm; Nếu đề cho ít hơn các mốc trên thì bài toán không giải được. Việc chứng minh phức tạp xin miễn trình bày..
* Một tình tiết nữa là thường Đề chỉ ra điều kiện số lần cân, không ra điều kiện dùng cân loại gì. Mặc dù thuật toán này chỉ ứng dụng cho loại cân 2 đĩa (Cân Roberrvan), không cần dùng quả cân, bài toán cổ mà!
4. Bài toán thực hành:
Bài 1: Có 16 viên bi giống nhau về hình thể, màu sắc, kích thước; nhưng 1 viên nhẹ cân. Hãy trình bày cách phát hiện viên bi nhẹ cân với không quá 3 lần cân.
Bài 2: Có một túi đường nặng 17kg. Bằng chiếc cân đĩa và một quả cân nặng 1kg, làm thế nào để lấy được 3,5kg đường từ túi đó?

