Giáo án dạy thêm môn Toán 9 theo công văn 3280
Giáo án điện tử môn Toán 9
Thư viện Đề thi - Trắc nghiệm - Tài liệu học tập miễn phí
Trang chủ: https://vndoc.com/ | Email hỗ trợ: hotro@vndoc.com | Hotline: 024 2242 6188
LUYỆN TẬP
CĂN THỨC BẬC HAI VÀ HẰNG ĐẲNG THỨC
2
A A
A./ KIẾN THỨC CƠ BẢN:
1. Căn bậc hai
- Định nghĩa: Căn bậc hai của số thực a là số x sao cho x
2
= a
- Chú ý:
+ Mỗi số thực a > 0, có 2 căn bậc hai là 2 số đối nhau số dương
a
, số âm
a
+ Số 0 có căn bậc hai là chính nó:
0 0
+ Số thực a < 0 không có căn bậc hai (tức
a
không có nghĩa khi a < 0)
2. Căn bậc hai số học
- Định nghĩa: Với
0a
thì số
x a
được gọi là căn bậc hai số học của a. Số 0 cũng
được gọi là căn bậc hai số học của 0
- Chú ý: Việc tìm căn bậc hai số học của 1 số không âm được gọi là phép khai phương
- Định lý: Với a, b > 0, ta có:
+ Nếu
a < b a b
+ Nếu
a a < bb
3. Căn thức bậc hai
- Cho A là 1 biểu thức thì biểu thức
A
được gọi là căn thức bậc hai của A ; A được gọi
là biểu thức lấy căn hay biểu thức dưới dấu căn
-
A
có nghĩa (hay xác định hay tồn tại)
0A
4. Hằng đẳng thức
2
A A
- Định lý : Với mọi số thực a, ta có :
2
a a
- Tổng quát : Với A là biểu thức, ta có :
2
êu A 0
-Anêu A<0
A n
A A
B./ BÀI TẬP ÁP DỤNG
Dạng 1 : Tìm căn bậc hai, căn bậc hai số học
* Phương pháp :
- Viết số đã cho dưới dạng bình phương của một số
- Tìm căn bậc hai số học của số đã cho
- Xác định căn bậc hai của số đã cho
Bài 1 : Tìm căn bậc hai của các số sau : 121 ; 144 ; 324 ;
1
; 3 2 2
64
G
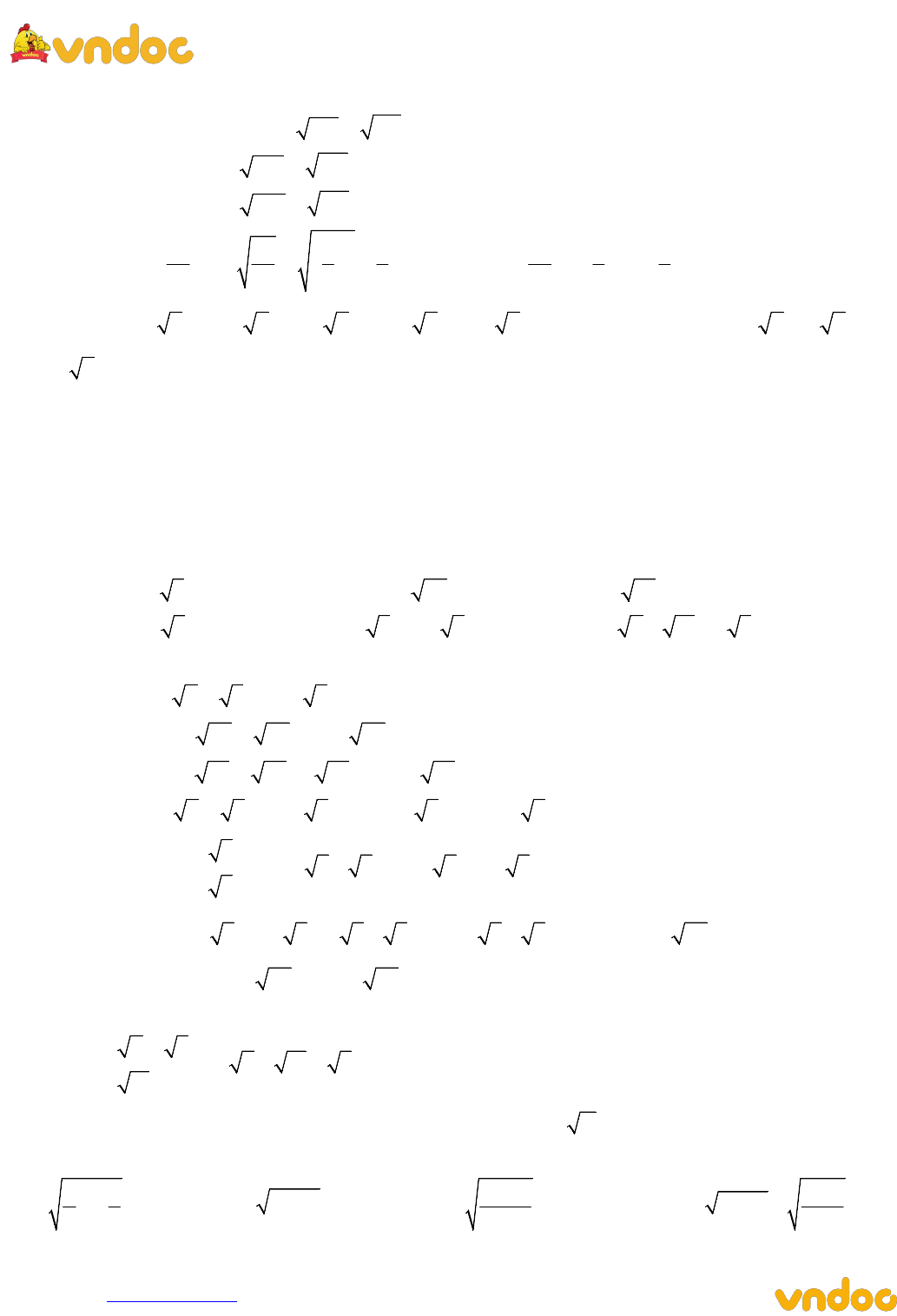
Thư viện Đề thi - Trắc nghiệm - Tài liệu học tập miễn phí
Trang chủ: https://vndoc.com/ | Email hỗ trợ: hotro@vndoc.com | Hotline: 024 2242 6188
+ Ta có CBHSH của 121 là :
2
121 11 11
nên CBH của 121 là 11 và -11
+ CBHSH của 144 là :
2
144 12 12
nên CBH của 121 là 12 và -12
+ CBHSH của 324 là :
2
324 18 18
nên CBH của 324 là 18 và -18
+ CBHSH của
1
64
là :
2
1 1 1
64 8 8
nên CBH của
1
64
là
1
8
và
1
8
+ Ta có :
2
3 2 2 2 2 2 1 2 1 2 1( 2 1 0)vi
nên CBH của
3 2 2
là
2 1
và
2 1
Dạng 2 : So sánh các căn bậc hai số học
* Phương pháp :
- Xác định bình phương của hai số
- So sánh các bình phương của hai số
- So sánh giá trị các CBHSH của các bình phương của hai số
Bài 2 : So sánh
a) 2 và
3
b) 7 và
47
c)
2 33
và 10
d) 1 và
3 1
e)
3 à 5- 8v
g)
2 11 à 3 5v
G
a) Vì 4 > 3 nên
4 3 2 3
b) Vì 49 > 47 nên
49 47 7 47
c) Vì 33 > 25 nên
33 25 33 5 2 33 10
d) Vì 4 > 3 nên
4 3 2 3 2 1 3 1 1 3 1
e) * Cách 1: Ta có:
3 2
3 8 5 3 5 8
8 3
* Cách 2: Giả sử
2
2
3 5 8 3 8 5 3 8 5 3 2 24 8 25
2 24 14 24 7 24 49
Bất đẳng thức cuối cùng đúng do đó bất đẳng thức đầu tiên đúng
g) Ta có:
2 3
2 11 3 5
11 5
Dạng 3: Tìm điều kiện để căn thức xác định:
A
xác định
0A
Bài 3: Tìm điều kiện của x để các biểu thức sau xác định
2
2 1 1 2
) ) 2 ) ) 3 5
3 5 2 3 4
x
a x b x c d x
x x
G
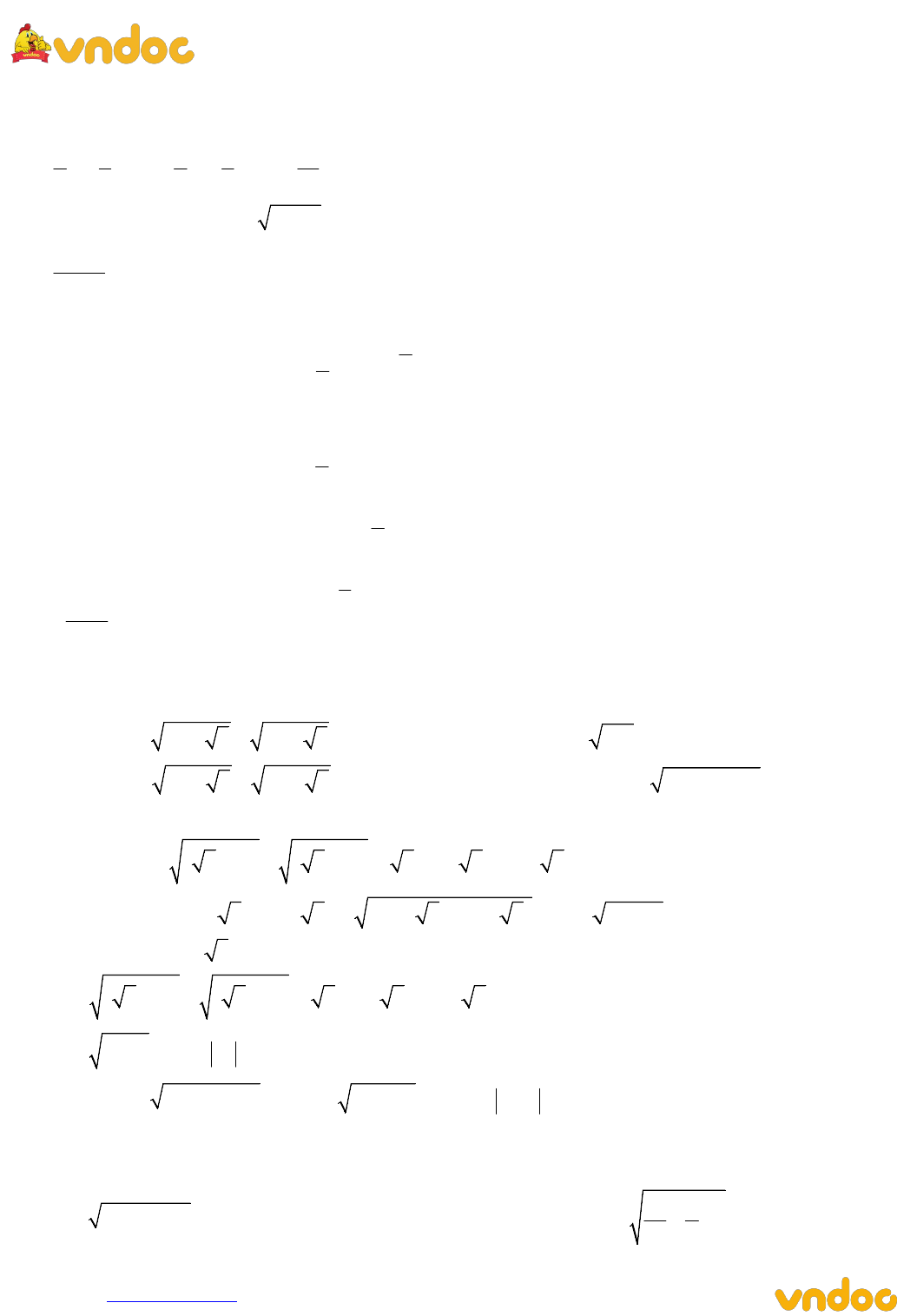
Thư viện Đề thi - Trắc nghiệm - Tài liệu học tập miễn phí
Trang chủ: https://vndoc.com/ | Email hỗ trợ: hotro@vndoc.com | Hotline: 024 2242 6188
Để các căn thức trên có nghĩa thì
a)
2 1 2 1 3
0
3 5 3 5 10
x x x
b) Ta có:
2 2
2 0, 2x x x
xác định với mọi x
c)
1 0
1
0
2 3 0
2 3
x
x
x
x
hoặc
1 0
2 3 0
x
x
+ Với
1
1 0
3
3
2 3 0
2
2
x
x
x
x
x
+ Với
1
1 0
1
3
2 3 0
2
x
x
x
x
x
Vậy căn thức xác định nếu
3
2
x
hoặc
1x
d)
3 5 0 5
3 5 0
4
3
2
4 0
0
4
4
x
x
x
x
x
x
x
Dạng 4 : Rút gọn biểu thức
Bài 4: Rút gọn các biểu thức sau:
a)
4 2 3 4 2 3A
c)
2
9 2 ( 0)C x x x
b)
6 2 5 6 2 5B
d)
2
4 16 8 ( 4)D x x x x
LG
a) Cách 1 :
2 2
3 1 3 1 3 1 3 1 2 3A
Cách 2 :
2
4 2 3 4 2 3 2 (4 2 3).(4 2 3) 8 2 16 12 8 2.2 12
2 3
A
A
b)
2 2
5 1 5 1 5 1 5 1 2 5B
c)
2
3 2 3 2 3 2 5 ( 0)C x x x x x x x vi x
d)
2 2
4 16 8 4 (4 ) 4 4 4 4 2( 4)( i 4)D x x x x x x x x x x v x
Dạng 5 : Tìm Min, Max
Bài 5 : Tìm Min
2
2
) 2 5 ) 1
4 6
x x
a y x x b y
Giáo án môn Toán 9 theo công văn 3280
Giáo án dạy thêm môn Toán 9 theo công văn 3280 được VnDoc sưu tầm và đăng tải với nội dung được biên soạn kỹ lưỡng, trình bày khoa học giúp các em học sinh dễ nắm được bài giảng. Sau đây là tài liệu mời quý thầy cô tham khảo
- Kế hoạch bài dạy theo mẫu công văn 5512
- Kế hoạch giảng dạy môn Ngữ văn 9 theo công văn 5512
- Mẫu giáo án minh họa môn Hóa học mô đun 2 THCS
- Mẫu giáo án minh họa môn Giáo dục thể chất mô đun 2 THCS
- Mẫu giáo án minh họa môn Địa lý mô đun 2 THCS
- Mẫu giáo án minh họa môn Sinh học mô đun 2 THCS
- Mẫu giáo án minh họa môn Công nghệ mô đun 2 THCS
- Mẫu giáo án minh họa môn Lịch sử mô đun 2 THCS
- Tổng hợp Mẫu giáo án minh họa mô đun 2 THCS
- Mẫu giáo án minh họa môn Tin học mô đun 3 THCS
- Kế hoạch giảng dạy môn Ngữ văn 9 theo công văn 5512
- Tổng hợp giáo án Địa 9 theo Công văn 5512
- Trọn bộ Phiếu bài tập theo tuần Toán 9
Mời quý thầy cô tham khảo thêm: Thư viện Giáo Án điện tử VnDoc
