3 bạn An, Mai và Bình viết biểu thức biểu thị tổng diện tích S của các phần tô màu trong Hình 1
Khám phá 1 trang 18 Toán 8 Tập 1 Chân trời sáng tạo
a) Ba bạn An, Mai và Bình viết biểu thức biểu thị tổng diện tích S của các phần tô màu trong Hình 1 như sau:
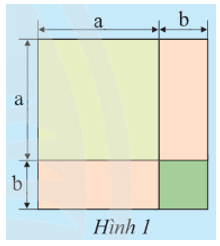
An: S = (a + b)2.
Mai: S = a2 + b2 + ab + ba.
Bình: S = a2 + 2ab + b2.
Kết quả của mỗi bạn có đúng không? Giải thích.
b) Thực hiện phép nhân và rút gọn đa thức của bạn An.
c) Bằng cách làm tương tự ở câu b), có thể biến đổi biểu thức (a − b)2 thành biểu thức nào?
Xác thực tài khoản!
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
Số điện thoại chưa đúng định dạng!
Xóa
Đăng nhập để viết
3 Câu trả lời
-
 Bé Cún0 Trả lời · 06/11/24
Bé Cún0 Trả lời · 06/11/24 -
 Bé Gạo0 Trả lời · 06/11/24
Bé Gạo0 Trả lời · 06/11/24 -
 Bọ Cạp0 Trả lời · 06/11/24
Bọ Cạp0 Trả lời · 06/11/24













