Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

VnDoc.com

Bài tập ôn tập chương 3: Phương trình bậc nhất một ẩn

Đề cương ôn tập chương 3 Đại số lớp 8

Đề cương ôn tập chương 3: Phương trình bậc nhất một ẩn Toán lớp 8

A. Lý thuyết cần nhớ trong chương 3: Phương trình bậc nhất một ẩn
B. Các bài tập về giải bài toán bài tập ôn tập chương 3
C. Hướng dẫn giải bài tập ôn tập chương 3

Đề cương ôn tập chương 3 đại số Toán 8 được VnDoc biên soạn và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán lớp 8 hiệu quả hơn. Mời các bạn tham khảo.

Đây là Đề cương ôn tập chương 3 đại số, được chia làm 2 dạng chính là Giải phương trình và Giải bài toán bằng cách lập phương trình, các phần bài tập được biên soạn theo chuẩn khung chương trình đào tạo của Bộ Giáo Dục ban hành. Qua đó sẽ giúp các bạn học sinh kiểm tra kiến thức cũng như củng cố lại các kiến thức đã được học về chương 3: Phương trình bậc nhất một ẩn. Đồng thời đây cũng là tài liệu để các bạn học sinh có thể tham khảo và ôn luyện chuẩn bị cho kì thi học kỳ 2 sắp tới.

Bài tập chương 3 Toán lớp 8: Phương trình bậc nhất một ẩn

A. Lý thuyết cần nhớ trong chương 3: Phương trình bậc nhất một ẩn

Ôn tập các câu hỏi ôn tập trong SGK trang 33

Câu 1: Thế nào là hai phương trình tương đương?

Câu 2: Nhân hai vế của phương trình cùng một biểu thức chứa ẩn thì có thể không được phương trình tương đương. Em hãy cho một ví dụ.

Câu 3: Với điều kiện nào của a thì phương trình ax + b = 0 là một phương trình bậc nhất? (a và b là hai hằng số)

Câu 4: Một phương trình bậc nhất một ẩn có mấy nghiệm?

Câu 5: Khi giải phương trình chứa ẩn ở mẫu, ta phải chú ý điều gì?

Câu 6: Hãy nêu các bước giải bài toán bằng cách lập phương trình

B. Các bài tập về giải bài toán bài tập ôn tập chương 3

I. Bài tập trắc nghiệm: Khoanh vào chữ cái đặt trước câu trả lời đúng

Câu 1: Nghiệm của phương trình $x\left( {x - 3} \right) - \left( {x + 2} \right)\left( {x - 1} \right) = 3$ $x\left( {x - 3} \right) - \left( {x + 2} \right)\left( {x - 1} \right) = 3$là:

A.$x = 4$ B. $x = - \frac{1}{4}$ $x = - \frac{1}{4}$ C.$x = - 4$ D. $x = \frac{1}{4}$ $x = \frac{1}{4}$

Câu 2: Nghiệm của phương trình $4x\left( {x - 1} \right) - \left( {2x + 2} \right)\left( {x - 1} \right) = 0$ $4x\left( {x - 1} \right) - \left( {2x + 2} \right)\left( {x - 1} \right) = 0$ là

A.$x = 1$ B. Vô nghiệm C. Vô số nghiệm D. $x = 2;\,\,x = 1$ $x = 2;\,\,x = 1$

Câu 3: Phương trình ${x^2} - 1 + \left( {x - 1} \right)\left( {x + 5} \right) = 0$ ${x^2} - 1 + \left( {x - 1} \right)\left( {x + 5} \right) = 0$ có số nghiệm là:

A. 1 nghiệm B. 2 nghiệm C. Vô nghiệm D. Vô số nghiệm

Câu 4: Phương trình $3x - 1 = 2\left( {x - 1} \right)$ $3x - 1 = 2\left( {x - 1} \right)$ tương đương với phương trình nào?

A. ${x^2} - 1 = 0$ ${x^2} - 1 = 0$ B. $x\left( {x - 1} \right) = 0$ $x\left( {x - 1} \right) = 0$

C. $\left| {x + 1} \right| = 0$ $\left| {x + 1} \right| = 0$ D. $\frac{{x + 3}}{{x - 1}} = 2$ $\frac{{x + 3}}{{x - 1}} = 2$

Câu 5: Cho 3 phương trình. Tìm phát biểu đúng trong các phát biểu dưới đây:

(I) $\frac{{x + 3}}{{x - 1}} = 2$ $\frac{{x + 3}}{{x - 1}} = 2$ (II) $\left( {x - 2} \right)\left( {x + 2} \right)\left( {x + 1} \right) = 0$ $\left( {x - 2} \right)\left( {x + 2} \right)\left( {x + 1} \right) = 0$ (III) $\frac{{\left( {{x^2} - 4} \right)\left( {x + 1} \right)}}{{x + 2}} = 0$ $\frac{{\left( {{x^2} - 4} \right)\left( {x + 1} \right)}}{{x + 2}} = 0$

A.(I) và (II) tương đương B. (I) và (III) tương đương

C. (I), (II), (III) tương đương D. (I), (II), (III) không tương đương nhau

Câu 6: Xác định m để phương trình $3x + m = x - 1$ nhận $x = - 3$ làm nghiệm:

A. -3 B. 3 C. -5 D. 5

Câu 7: Điều kiện xác định của phương trình $\frac{{x + 2}}{{x - 2}} - \frac{1}{x} = \frac{2}{{{x^2} - 2x}}$ $\frac{{x + 2}}{{x - 2}} - \frac{1}{x} = \frac{2}{{{x^2} - 2x}}$là:

A. $x \ne 2$ $x \ne 2$ B. $x \ne 0$ $x \ne 0$ C. $\left\{ \begin{array}{l} x \ne 2\\ x \ne 0 \end{array} \right.$ $\left\{ \begin{array}{l} x \ne 2\\ x \ne 0 \end{array} \right.$ D. $\left[ \begin{array}{l} x \ne 2\\ x \ne 0 \end{array} \right.$ $\left[ \begin{array}{l} x \ne 2\\ x \ne 0 \end{array} \right.$

II. Bài tập tự luận

Bài 1: Giải các phương trình:

a, ${\left( {x - 1} \right)^2} - {\left( {x + 1} \right)^2} = 2\left( {x - 3} \right)$ ${\left( {x - 1} \right)^2} - {\left( {x + 1} \right)^2} = 2\left( {x - 3} \right)$

b, ${\left( {2x - 1} \right)^2} - {\left( {2x + 1} \right)^2} = 4\left( {x - 3} \right)$ ${\left( {2x - 1} \right)^2} - {\left( {2x + 1} \right)^2} = 4\left( {x - 3} \right)$

c, ${\left( {2x + 3} \right)^2} - 3\left( {x - 4} \right)\left( {x + 4} \right) = {\left( {x - 2} \right)^2}$ ${\left( {2x + 3} \right)^2} - 3\left( {x - 4} \right)\left( {x + 4} \right) = {\left( {x - 2} \right)^2}$

d, $x\left( {x + 1} \right) - \left( {x - 3} \right)\left( {x - 4} \right) = 5x$ $x\left( {x + 1} \right) - \left( {x - 3} \right)\left( {x - 4} \right) = 5x$

e, $\frac{x}{{10}} - \left( {\frac{x}{{30}} + \frac{{2x}}{{45}}} \right) = \frac{4}{5}$ $\frac{x}{{10}} - \left( {\frac{x}{{30}} + \frac{{2x}}{{45}}} \right) = \frac{4}{5}$

f, $\frac{{5\left( {2x - 1} \right)}}{{18}} + \frac{{x + 3}}{{12}} = \frac{{7x + 3}}{6} - \frac{{2\left( {3 - x} \right)}}{9}$ $\frac{{5\left( {2x - 1} \right)}}{{18}} + \frac{{x + 3}}{{12}} = \frac{{7x + 3}}{6} - \frac{{2\left( {3 - x} \right)}}{9}$

g, $\frac{{x + 4}}{5} - x - 5 = \frac{{x + 3}}{3} - \frac{{x - 2}}{2}$ $\frac{{x + 4}}{5} - x - 5 = \frac{{x + 3}}{3} - \frac{{x - 2}}{2}$

h, $\frac{{3x - 5}}{{10}} - \frac{{2x + 1}}{3} = x + \frac{{x - 9}}{5} - \frac{{5x + 3}}{6}$ $\frac{{3x - 5}}{{10}} - \frac{{2x + 1}}{3} = x + \frac{{x - 9}}{5} - \frac{{5x + 3}}{6}$

Bài 2: Giải các phương trình:

a, ${x^2} - 9 = \left( {x - 3} \right)\left( {5x + 2} \right)$ ${x^2} - 9 = \left( {x - 3} \right)\left( {5x + 2} \right)$

b, ${x^3} - 1 = \left( {x - 1} \right)\left( {{x^2} - 2x + 16} \right)$ ${x^3} - 1 = \left( {x - 1} \right)\left( {{x^2} - 2x + 16} \right)$

c, $4{x^2}\left( {x - 1} \right) - x + 1 = 0$ $4{x^2}\left( {x - 1} \right) - x + 1 = 0$

d, ${x^3} + 4{x^2} - 9x - 36 = 0$ ${x^3} + 4{x^2} - 9x - 36 = 0$

e, ${\left( {3x + 5} \right)^2} = {\left( {x - 1} \right)^2}$ ${\left( {3x + 5} \right)^2} = {\left( {x - 1} \right)^2}$

f, $9{\left( {2x + 1} \right)^2} = 4{\left( {x - 5} \right)^2}$ $9{\left( {2x + 1} \right)^2} = 4{\left( {x - 5} \right)^2}$

g, ${x^2} + 2x = 15$ ${x^2} + 2x = 15$

h, ${x^4} - 5{x^3} + 4{x^2} = 0$ ${x^4} - 5{x^3} + 4{x^2} = 0$

i, $\left( {3x + 2} \right)\left( {{x^2} - 1} \right) = \left( {9{x^2} - 4} \right)\left( {x + 1} \right)$ $\left( {3x + 2} \right)\left( {{x^2} - 1} \right) = \left( {9{x^2} - 4} \right)\left( {x + 1} \right)$

k, $\left( {{x^2} - 4} \right) - \left( {x - 2} \right)\left( {3 - 2x} \right) = 0$ $\left( {{x^2} - 4} \right) - \left( {x - 2} \right)\left( {3 - 2x} \right) = 0$

l, $\left( {3x - 1} \right)\left( {{x^2} + 2} \right) = \left( {3x - 1} \right)\left( {7x - 10} \right)$ $\left( {3x - 1} \right)\left( {{x^2} + 2} \right) = \left( {3x - 1} \right)\left( {7x - 10} \right)$

m, $\left( {2{x^2} + 1} \right)\left( {4x - 3} \right) = \left( {x - 12} \right)\left( {2{x^2} + 1} \right)$ $\left( {2{x^2} + 1} \right)\left( {4x - 3} \right) = \left( {x - 12} \right)\left( {2{x^2} + 1} \right)$

Bài 3: Giải các phương trình:

a, $\frac{{x - 2}}{{x + 3}} - \frac{{x + 2}}{{x - 3}} = \frac{{{x^2} + 1}}{{{x^2} - 9}} - 1$ $\frac{{x - 2}}{{x + 3}} - \frac{{x + 2}}{{x - 3}} = \frac{{{x^2} + 1}}{{{x^2} - 9}} - 1$

b, $\frac{{3x}}{{x - 2}} - \frac{x}{{x - 5}} - \frac{{2{x^2}}}{{{x^2} - 7x + 10}} = 0$ $\frac{{3x}}{{x - 2}} - \frac{x}{{x - 5}} - \frac{{2{x^2}}}{{{x^2} - 7x + 10}} = 0$

c, $\frac{{13}}{{\left( {x - 3} \right)\left( {2x + 7} \right)}} + \frac{1}{{2x + 7}} = \frac{6}{{{x^2} - 9}}$ $\frac{{13}}{{\left( {x - 3} \right)\left( {2x + 7} \right)}} + \frac{1}{{2x + 7}} = \frac{6}{{{x^2} - 9}}$

d, $\frac{2}{{ - {x^2} + 6x - 8}} - \frac{{x - 1}}{{x - 2}} = \frac{{x + 3}}{{x - 4}}$ $\frac{2}{{ - {x^2} + 6x - 8}} - \frac{{x - 1}}{{x - 2}} = \frac{{x + 3}}{{x - 4}}$

Bài 4: Giải các phương trình:

a, ${x^4} - 5{x^2} + 4 = 0$ ${x^4} - 5{x^2} + 4 = 0$

b, ${\left( {{x^2} + 5x} \right)^2} - 2\left( {{x^2} + 5x} \right) = 24$ ${\left( {{x^2} + 5x} \right)^2} - 2\left( {{x^2} + 5x} \right) = 24$

c, $x\left( {x + 1} \right)\left( {x - 1} \right)\left( {x + 2} \right) = 24$ $x\left( {x + 1} \right)\left( {x - 1} \right)\left( {x + 2} \right) = 24$

d, ${x^4} + 2{x^3} + 5{x^2} + 4x - 12 = 0$ ${x^4} + 2{x^3} + 5{x^2} + 4x - 12 = 0$

Bài 5:

1, Giải và biện luận các phương trình sau (với m là tham số)

a, $mx - x - m + 2 = 0$

b, ${m^2}x + 3mx - {m^2} + 9 = 0$ ${m^2}x + 3mx - {m^2} + 9 = 0$

c, ${m^3}x - {m^2} - 4 = 4m\left( {x - 1} \right)$ ${m^3}x - {m^2} - 4 = 4m\left( {x - 1} \right)$

2, Cho phương trình ẩn x: $\left( {5{k^3} - 4{k^2} + 2k} \right)x = 4{k^3} + 3{k^2} + k$ $\left( {5{k^3} - 4{k^2} + 2k} \right)x = 4{k^3} + 3{k^2} + k$. Hãy xác định các giá trị của để phương trình trên có nghiệm .

3, Hãy xác định giá trị của để mỗi phương trình sau vô nghiệm:

a, $mx + x - m - 2 = 0$

b, ${m^2}x - 5mx - {m^2} + 25 = 0$ ${m^2}x - 5mx - {m^2} + 25 = 0$

c, $\frac{{x + m}}{{x + 1}} = \frac{{x + 2}}{x}$ $\frac{{x + m}}{{x + 1}} = \frac{{x + 2}}{x}$

Bài 6: Một người đi xe máy từ A đến B với vận tốc 25 km/h. Lúc từ B trở về A người đó đi với vận tốc 30 km/h nên thời gian về ít hơn thời gian đi là 30 phút. Hãy tính độ dài quãng đường AB và thời gian lúc về.

Bài 7: Lúc 6 giờ, một ô tô xuất phát từ A đến B với vận tốc trung bình 40 km/h. Khi đến B, người lái xe làm nhiệm vụ giao nhận hàng trong 30 phút rồi cho xe quay trở về A với vận tốc trung bình 30 km/h. Tính độ dài quãng đường AB biết rằng ô tô về đến A lúc 10 giờ cùng ngày.

Bài 8: Một xe máy đi từ A đến B với vận tốc 36 km/h. Sau đó 30 phút, một ô tô cũng đi từ A đến B với vận tốc 48 km/h. Tính độ dài quãng đường AB, biết cả hai xe đến B cùng một lúc.

Bài 9: Lúc 7h một người đi xe máy từ A đến B với vận tốc 40 km/h, đến 8h30 cùng ngày một người khác đi xe máy từ B đến A với vận tốc 60 km/h. Hỏi hai người gặp nhau lúc mấy giờ, biết quãng đường AB dài 120 km.

Bài 10: Một ca nô xuôi dòng từ bến A đến bến B với vận tốc 30 km/h, sau đó lại ngược từ B trở về A. Thời gian đi xuôi ít hơn thời gian đi ngược là 40 phút. Hãy tính khoảng cách giữa hai bến A và B, biết rằng vận tốc của dòng nước là 3 km/h và vận tốc thật của ca nô không đổi.

Bài 11: Một ca nô tuần tra đi xuôi dòng từ A đến B hết 1 giờ 20 phút và ngược dòng từ B về A hết 2 giờ. Tính vận tốc riêng của ca nô, biết vận tốc dòng nước là 3 km/h.

Bài 12: Một phân xưởng được giao sản xuất một lô sản phẩm đã lập kế hoạch mỗi ngày phải sản xuất 50 sản phẩm. Nhưng do biết phân công hợp lý nên phân xưởng đã sản xuất được mỗi ngày thêm 15 sản phẩm, nên không những đã hoàn thành kế hoạch trước dự định 3 ngày mà còn vượt mức được 255 sản phẩm. Hỏi theo kế hoạch phân xưởng đã phải sản xuất bao nhiêu sản phẩm?

Bài 13: Một người dự định sản xuất 120 sản phẩm trong một thời gian nhất định. Do tăng năng suất 4 sản phẩm mỗi giờ nên người đó đã hoàn thành sớm hơn dự định 1 giờ. Hãy tính năng suất dự kiến.

Bài 14: Tìm số tự nhiên có hai chữ số, biết chữ số hàng chục kém chữ số hàng đơn vị là 3. Nếu đem chia số đó cho tổng các chữ số của nó thì được thương là 4 và dư 3.

Một khu vườn hình chữ nhật có chiều dài gấp hai lần chiều rộng. Nếu tăng chiều rộng 4m và giảm chiều dài 6m thì diện tích của khu vườn không thay đổi. Tìm chu vi của khu vườn lúc đầu.

C. Hướng dẫn giải bài tập ôn tập chương 3

I. Bài tập trắc nghiệm

Câu 1	Câu 2	Câu 3	Câu 4	Câu 5	Câu 6	Câu 7
B	A	B	C	D	D	C

II. Bài tập tự luận

Bài 1:

a, $S = \left\{ 1 \right\}$ $S = \left\{ 1 \right\}$ b, $S = \left\{ 1 \right\}$ $S = \left\{ 1 \right\}$ c, $S = \left\{ { - \frac{{53}}{{16}}} \right\}$ $S = \left\{ { - \frac{{53}}{{16}}} \right\}$ d, $S = \left\{ 4 \right\}$ $S = \left\{ 4 \right\}$

e, $S = \left\{ {36} \right\}$ $S = \left\{ {36} \right\}$ f, $S = \left\{ {\frac{5}{{27}}} \right\}$ $S = \left\{ {\frac{5}{{27}}} \right\}$ g, $S = \left\{ {\frac{{ - 286}}{{19}}} \right\}$ $S = \left\{ {\frac{{ - 286}}{{19}}} \right\}$ h, $S = \left\{ 2 \right\}$ $S = \left\{ 2 \right\}$

Bài 2:

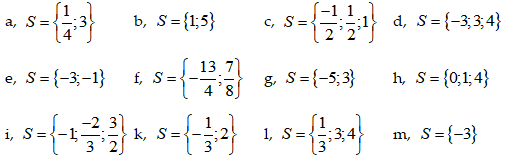
bài tập ôn tập chương 3 đại số 8 ảnh số 1

Bài 3:

a, $S = \left\{ { - 1} \right\}$ $S = \left\{ { - 1} \right\}$ b, $S = \left\{ 0 \right\}$ $S = \left\{ 0 \right\}$ c, $S = \left\{ { - 4} \right\}$ $S = \left\{ { - 4} \right\}$ d, $S = \left\{ {0;2} \right\}$ $S = \left\{ {0;2} \right\}$

Bài 4:

a, $S = \left\{ { - 2; - 1;1;2} \right\}$ $S = \left\{ { - 2; - 1;1;2} \right\}$. HD: đặt $t = {x^2}$ $t = {x^2}$

b, $S = \left\{ { - 6; - 4; - 1;1} \right\}$ $S = \left\{ { - 6; - 4; - 1;1} \right\}$. HD: đặt $t = {x^2} + 5x$ $t = {x^2} + 5x$

c, $S = \left\{ { - 3;2} \right\}$ $S = \left\{ { - 3;2} \right\}$. HD: đặt $t = {x^2} + x$ $t = {x^2} + x$

d, $S = \left\{ { - 2} \right\}$ $S = \left\{ { - 2} \right\}$. HD: phân tích đa thức thành nhân tử

Bài 5:

1, Học sinh tự giải đáp bằng lý thuyết

Phương trình bậc nhất ax + b = 0 có nghiệm khi a khác 0; vô nghiệm khi a = 0 và b khác 0; vô số nghiệm khi a = 0 và b = 0

2, k = 1

3, Học sinh tự giải đáp

------------------------

Ngoài Đề cương ôn tập chương 3 Đại số, mời các bạn học sinh tham khảo thêm các đề thi học kì 2 Toán 8, đề kiểm tra học kì 2 các môn lớp 8 như Anh, Văn, Địa lý,... mà chúng tôi đã sưu tầm và chọn lọc. Với Đề cương ôn tập chương 3 đại số này sẽ giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn học tập tốt!

Chia sẻ, đánh giá bài viết

14.752