Đề ôn thi học kì 1 môn Toán lớp 6 - Đề 1
Đề ôn thi học kì 1 môn Toán lớp 6 - Đề 1 được VnDoc sưu tầm, chọn lọc cho các em học sinh ôn tập, củng cố kiến thức, rèn luyện kỹ năng giải Toán chuẩn bị cho các bài thi kiểm tra học kì 1 lớp 6. Mời các thầy cô cùng các em học sinh tham khảo.
Đề ôn thi học kì 1 môn Toán lớp 6 - Đề 1
Đề bài: Đề ôn tập thi học kì 1 môn Toán lớp 6
Bài 1 (2,5 điểm).
Tính:
a) A = ( - 1436) - ( - 1586 + |- 532|) - (568 + 468) + 1434
b) B = 
\(\dfrac{{{{18}^6}{{.2}^{12}}{{.4}^3}{{.9}^3}}}{{{{16}^3}{{.6}^9}{{.27}^3}}}\)
Bài 2 (2 điểm).
a) Tìm số nguyên x sao cho:\({\left| { - 2} \right|^{10}} - (x + 24) = 80 - \left[ {( - 4){{.5}^2} + {2^4}.5} \right]\)
b) Tìm các cặp số nguyên (x;y) sao cho: | x - 4| + | y + 5| = 1
Bài 3 (2,0 điểm).
Số học sinh khối THCS của trường THPT Chuyên Hà Nội – Amsterdam tham gia thi độ nghi thức trong khoảng từ 800 đến 1000 em, được xếp thành các hàng. Nếu xếp mỗi hàng 20 thì dư 9 em; nếu xếp mỗi hàng 30 thì thiếu 21 em; nếu xếp mỗi hàng 35 thì thiếu 26 em. Hỏi có tất cả bao nhiêu em dự thi nghi thức đội?
Bài 4 (2,5 điểm).
Cho đoạn thẳng AB có độ dài 9cm, điểm C thuộc đoạn thẳng AB sao cho AC = 3cm. Điểm D nằm giữa hai điểm B và C sao cho CD = 1/3 DB.
a) Tính độ dài của các đoạn thẳng CB, CD và AD.
b) Chứng minh điểm D là trung điểm của AB.
Bài 5 (1 điểm).
a) Tìm số tự nhiên a nhỏ nhất sao cho khi a chia cho 5; cho 7; cho 9 có số dư theo thứ tự là 4; 2; 7.
b) (Dành riêng cho lớp 6A) Tính: A =\({1.2^2} + {2.3^2} + {3.4^2} + \cdot \cdot \cdot + {2017.2018^2}\)
Đáp án và Hướng dẫn giải: Đề ôn tập học kì 1 môn Toán lớp 6
Bài 1.
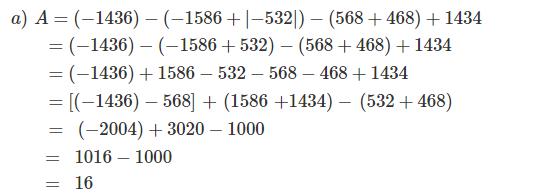
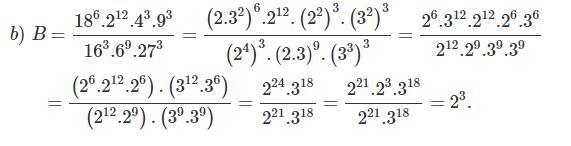
Bài 2:
\(\begin{array}{l}a)\;{\left| { - 2} \right|^{10}} - (x + 24) = 80 - \left[ {( - 4){{.5}^2} + {2^4}.5} \right]\\\;\;\;\;\;{2^{10}} - (x + 24)\;\;\; = 80 - \left[ {( - 4).25 + 16.5} \right]\\\;\;\;\;1024 - (x + 24) = 80 - \left[ { - 100 + 80} \right]\\\;\;\;\;1024 - x - 24 = 80 + 100 - 80\\\;\;\;\;1024 - 24 - x = 80 - 80 + 100\\\;\;\;\;\;1000 - x\;\;\;\;\;\;\; = 100\\\;\;\;\;\;x\;\;\;\;\;\;\; = 1000 - 100\\\;\;\;\;\;x\;\;\;\;\;\;\; = 900.\end{array}\)
b) Ta có: \(\{ \begin{array}{l}\left| {x - 4} \right| \ge 0\\\left| {y + 5} \right| \ge 0\end{array}\). (với mọi \(x \in \mathbb{Z},y \in \mathbb{Z}\))
Vì 1 = 1 + 0 = 0 + 1 nên suy ra\(\left\{ \begin{array}{l}\left| {x - 4} \right| = 0\\\left| {y + 5} \right| = 1\end{array} \right.hoặc \left\{ \begin{array}{l}\left| {x - 4} \right| = 1\\\left| {y + 5} \right| = 0\end{array} \right.\)
+) Trường hợp 1: \(\left\{ \begin{array}{l}\left| {x - 4} \right| = 1\\\left| {y + 5} \right| = 0\end{array} \right.\)
\(\left| {x - 4} \right| = 0 \Rightarrow x - 4 = 0 \Rightarrow x = 4\)
\(\left| {y + 5} \right| = 1 \Rightarrow y + 5 = 1\) hoặc \(y + 5 = 1 \Rightarrow y = - 4\) hoặc y = - 6
Với trường hợp 1 có hai cặp (x; y) thỏa mãn là x = 4;y = - 4 và x = 4;y = - 6.
+) Trường hợp 2:\(\left\{ \begin{array}{l}\left| {x - 4} \right| = 1\\\left| {y + 5} \right| = 0\end{array} \right.\)
\(\left| {x - 4} \right| = 1 \Rightarrow x - 4 = 1\) hoặc \(x - 4 = - 1 \Rightarrow x = 5\) hoặc x = 3
\(\left| {y + 5} \right| = 0 \Rightarrow y + 5 = 0 \Rightarrow y = - 5\)
Với trường hợp 2 có hai cặp (x; y) thỏa mãn là x = 3;y = - 5 và x = 5;y = - 5.
Vậy có 4 cặp số nguyên thỏa mãn yêu cầu đề bài:
\(\left( {x;\;y} \right) = \left\{ {\left( {4; - 4} \right);\;\left( {4; - 6} \right);\;\left( {3; - 5} \right);\;\left( {5; - 5} \right)} \right\}.\)
Bài 3
Gọi x là số học sinh dự thi nghi thức đội (800 < x < 1000).
Nếu xếp mỗi hàng 20 thì dư 9 em nên ta có (x - 9) ⋮ 20.
Nếu xếp mỗi hàng 30 thì thiếu 21 em, tức là nếu xếp mỗi hàng 30 thì sẽ dư 9 em, do đó (x - 9) ⋮ 30.
Nếu xếp mỗi hàng 35 thì thiếu 26 em, tức là nếu xếp mỗi hàng 35 thì sẽ dư 9 em, do đó (x - 9) ⋮ 35.
Vậy (x - 9) ⋮ 20; (x - 9) ⋮ 30; (x - 9) ⋮ 35 suy ra x - 9 ∈ BC (20;30;35)
Ta có: 20 = 22.5; 30 = 2.3.5; 35 = 5.7.
BCNN (20;30;35) = 22.3.5.7 = 420.
\(BC{\rm{ }}(20;{\rm{ 30}};{\rm{ 35}}) = B\left( {420} \right) = \left\{ {0;{\rm{ 420}};{\rm{ 840}};{\rm{ 126}}0;{\rm{ }} \ldots } \right\}\)
Do đó: \(x - 9 \in \left\{ {0;{\rm{ 42}}0;{\rm{ 84}}0;{\rm{ 126}}0;{\rm{ }} \ldots } \right\}\)
Suy ra \(x \in \left\{ {9;{\rm{ 429}};{\rm{ 849}};{\rm{ 1269}};{\rm{ }} \ldots } \right\}\)
Lại có 800 < x < 1000 nên x = 849 .
Vậy có tất cả 849 em dự thi nghi thức đội.
Bài 4:
a) Trên tia AB ta có AC < AD( {do 3cm < 9cm )nên C là điểm nằm giữa hai điểm A và B
AC + CB = AB
CB = AB - AC = 9 - 3 = 6(cm)
+) Vì điểm D nằm giữa hai điểm B và C nên CD + DB = BC (*)
Theo đề bài CD = 1/3 DB , thay vào (*) ta được:
1/3 DB +DB = BC
⇒4/3 DB = BC
⇒DB = 6 : 4/3 = 4,5(cm)
⇒CD = 1/3DB
=4,5 : 3 = 1,5cm
Trên tia BA ta cóBD < BA( {do 4,5cm < 9cm) nên D là điểm nằm giữa hai điểm B và A
BD + DA = BA DA = BA - BD = 9 - 4,5 = 4,5(cm)
AD = 4,5cm
b) Theo chứng minh trên ta có D là điểm nằm giữa hai điểm B và A.
Lại có AD = DB = 4,5cm.
Từ đó suy ra D là trung điểm của đoạn thẳng AB.
Bài 5.
a) Theo đề bài ta có:
a chia cho 5 dư 4 nên\(\left( {a - 4} \right)\; \vdots \;5 \Rightarrow 4\left( {a - 4} \right)\; \vdots \;5 \Leftrightarrow \left( {4a - 16} \right)\; \vdots \;5 \Rightarrow \left( {4a - 1} \right)\; \vdots \;5\)
a chia cho 7 dư 2 nên\(\left( {a - 2} \right)\; \vdots \;7 \Rightarrow 4\left( {a - 2} \right)\; \vdots \;7 \Leftrightarrow \left( {4a - 8} \right)\; \vdots \;7 \Rightarrow \left( {4a - 1} \right)\; \vdots \;7\)
a chia cho 9 dư 7 nên \(\left( {a - 7} \right)\; \vdots \;9 \Rightarrow 4\left( {a - 7} \right)\; \vdots \;9 \Leftrightarrow \left( {4a - 28} \right)\; \vdots \;9 \Rightarrow \left( {4a - 1} \right)\; \vdots \;9\)
(4a - 1) chia hết cho 5, 7, 9.
Hay ( 4a - 1) = BC( 5; 7; 9)
Mà a nhỏ nhất (4a - 1) = BCNN( {5; 7; 9) = 5.7.9 = 315.
4a - 1 = 315
4a = 316
a = 79.
Vậy a = 79 là số cần tìm.
>> Tham khảo đề tiếp theo: Đề ôn thi học kì 1 môn Toán lớp 6 - Đề 2
Đề ôn tập học kì 1 môn Toán lớp 6 - Đề 1 bao gồm 5 câu hỏi có đáp án đầy đủ cho từng câu hỏi cho các em học sinh tham khảo, ôn tập, hệ thống toàn bộ kiến thức đã học môn Toán lớp 6 học kì 1. Ngoài ra, các em học sinh tham khảo các bài giải SGK môn Toán lớp 6, Môn Ngữ văn 6, Môn Vật lý 6, môn Sinh Học 6, Địa lý 6, Lịch sử 6....và các đề thi học kì 1 lớp 6 để chuẩn bị cho các bài thi đề thi học kì 1 đạt kết quả cao.
