Đề thi giáo viên dạy giỏi môn Toán trường THCS Kim Liên năm 2018 - 2019
Đề thi giáo viên giỏi cấp trường bậc THCS môn Toán có đáp án
VnDoc - Tải tài liệu, văn bản pháp luật, biểu mẫu miễn phí
PHÒNG GD&ĐT NAM ĐÀN
TRƯỜNG THCS KIM LIÊN
(Đề thi có 01 trang)
HỘI THI GIÁO VIÊN DẠY GIỎI CẤP TRƯỜNG
NĂM HỌC 2018 – 2019
ĐỀ THI KIỂM TRA NĂNG LỰC
Môn: Toán
Thời gian làm bài 150 phút
Ngày thi: 06/12/2018
Câu 1. (2.5 điểm): Thầy (cô) hãy cho biết: Trong dạy học và kiểm tra đánh giá
theo hướng phát triển năng lực, cần chú trọng hình thành và phát triển cho học sinh
những phẩm chất và năng lực nào? Trình bày các năng lực cụ thể (chuyên biệt)
trong bộ môn thầy (cô) phụ trách? Cho một ví dụ minh họa.
Câu 2. (2.5 điểm): Hãy nêu mục đích, ý nghĩa của sinh hoạt chuyên môn theo
nghiên cứu bài học và các bước tiến hành.
Câu 3: ( 4điểm )
a) So sánh:
2019 2018
2019 2018
A
và
2 2
2 2
2019 2018
2019 2018
B
b) Tìm ba số x, y, z thỏa mãn:
3 4 5
x y z
và
2 2 2
2 8x y z
Câu 4 (4 điểm)
a) Cho A=1.2+2.3+3.4+…+2018.2019
So sánh A với
3
2019
3
b) Tìm số tự nhiên n để (n+3)(n+1) là số nguyên tố.
Câu 5: (3 điểm )
a) Chứng minh rằng với mọi số tự nhiên n thì số
N=
2 2 3
5.7 2
n n
chia hết cho 41.
b) Nếu tham gia bồi dưỡng học sinh giỏi, anh( chị) hãy giải và hướng dẫn
những ý cơ bản để học sinh giải được và hiểu đúng bài toán:
Tìm GTNN của A biết:
A
2 2
6 9 4 4x x x x
Câu6:( 4 điểm)
Cho đường tròn (O) và điểm M nằm bên ngoài đường tròn đó. Qua M kẻ tiếp tuyến
MT và cát tuyến MAB ( A nằm giữa M và B) với đường tròn. Gọi H là hình chiếu
của T trên MO, K là giao điểm của đoạn thẳng MO với đường tròn (O). Chứng
minh:
a)
2
.MT MA MB
b) KM.AH=KH.AM
---------------------------Hết-----------------------------
ĐỀ CHÍNH THỨC
VnDoc - Tải tài liệu, văn bản pháp luật, biểu mẫu miễn phí
ĐÁP ÁN MÔN TOÁN
KỲ THI GV GIỎI TRƯỜNG. NĂM HỌC 2018-2019
Câu
Nội dung đáp án
điểm
Câu 1
4 điểm
a)
2 2
2 2 2
(2019 2018)(2019 2018) 2019 2018
(2019 2018) 2019 2.2019.2018 2018
A
Vì
2 2
2019 2.2019.2018 2018
>
2 2
2019 2018
Nên
2 2
2 2
2019 2018
2019 2.2019.2018 2018
<
2 2
2 2
2019 2018
2019 2018
hay A<B
b)Ta có :
2 2 2
3 4 5 9 16 25
x y z x y z
Áp dụng T/C dãy tỷ số bằng nhau ta có:
2 2 2
9 16 25
x y z
=
2 2 2 2 2 2
2 8
4
9 16 25 9 32 25 2
x y z x y z
Vì x, y, z cùng dấu nên:
x=6, y=8, z=10
Hoặc x=-6, y=-8, z=-10
1 đ
0,5 đ
0,5 đ
0,5 đ
1 đ
0,5 đ
Câu 2
4 điểm
a)
3A=1.2.3+2.3.(4-1)+3.4.(5-2)+...+2018.2019.(2020-2017)
3A= 2018.2019.2020
2018.2019.2020
3
A
Ta có: 2018.2020=2018.( 2019+1)=2018.2019+2018
2019.2019=2019.(2018+1)=2018.2019+2019
Vì 2018.2019+2018<2018.2019+2019
Nên 2018.2020<2019.2019
2018.2019.2020<2019.2019.2019
3
2019
3
A
b)
Để tích (n+3)(n+1) là số nguyên tố thì một trong hai thừa số
phải bằng 1.
Mà n+3>n+1
1
1 1 0n n
Khi đó n+3=3 là số nguyên tố
Vậy n=0
0,5 đ
0,5 đ
0,5đ
0,5đ
0,5đ
0,5đ
Câu 3
3 điểm
a) N=
2 2 3
5.7 2
n n
=
0,5 đ
0,5 đ
VnDoc - Tải tài liệu, văn bản pháp luật, biểu mẫu miễn phí
1
1 1 1
1
5.49 8 5.49 5.8 41.8
5.(49 8 ) 41.8
n
n n n n n
n n
Vì
1 1
(49 8 ) (49 8)
n n
Suy ra 5.
1
1
(49 8 ) 41
n
n
mà
41.8 41
n
Nên N chia hết cho 41
b) GV nêu hệ thống câu hỏi để HD học sinh giải.
A=
2 2
6 9 4 4x x x x
A=
3 2 3 2x x x x
A
3 2 5A x x
Dấu “=” xẩy ra
(3 )( 2) 0 2 3x x x
Vậy GTNN của A là 5
2 3x
0,5 đ
0,5 đ
0,5 đ
Câu 4
4 điểm
a)
2
( )
.
MTA MBT gg
MT MA
MB MT
MT MA MB
(1)
b) Áp dụng hệ thức lượng trong tam giác vuông MTO ta có:
2
.MT MO MH
(2)
Từ (1) và (2) suy ra MA.MB=MO.MH
MB MH
MO MA
ˆ ˆ
( )MBO MHA cgc MHA MBO
Từ đó c/m đc tứ giác OHAB nội tiếp.
Gọi N là giao điểm thứ hai của MO với đường tròn (O).
C/m được:
ˆ
ˆ ˆ
MAK MNB OBN
(3)
1
ˆ ˆ
ˆ ˆ ˆ ˆ
2
2
MOB ONB OBN ONB ONB MOB
(4)
Mặt khác do tứ giác OHAB nội tiếp nên
ˆ ˆ
(5)MAH MOB
Từ (3), (4), (5) suy ra
1
ˆ ˆ
2
MAK MAH
1 đ
0,5đ
0,5 đ
0,25đ
0,25 đ
0,25 đ
0,5đ
0,5d
0,25d
N
K
H
O
B
A
T
M
Đề thi giáo viên dạy giỏi môn Toán cấp THCS
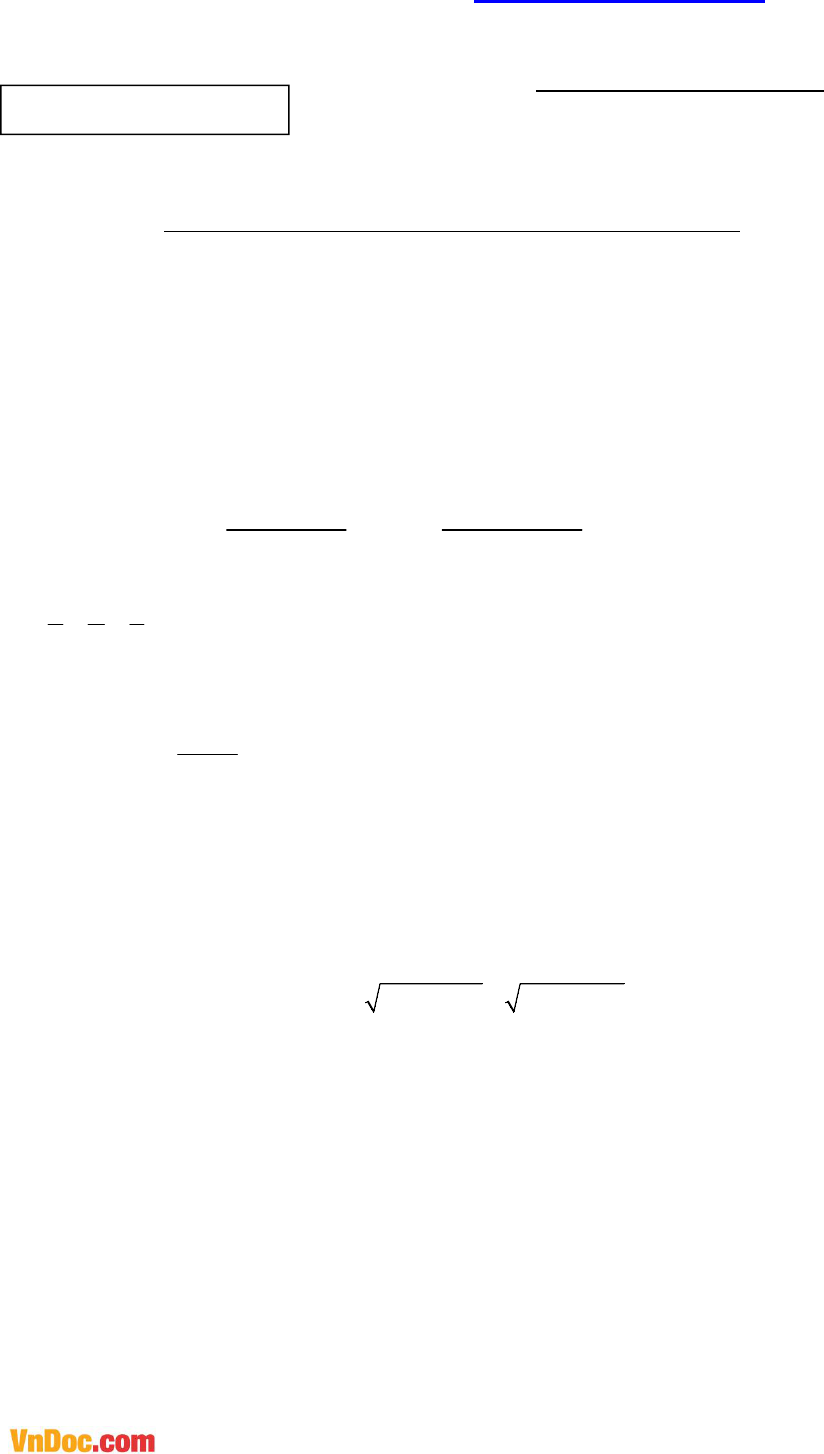
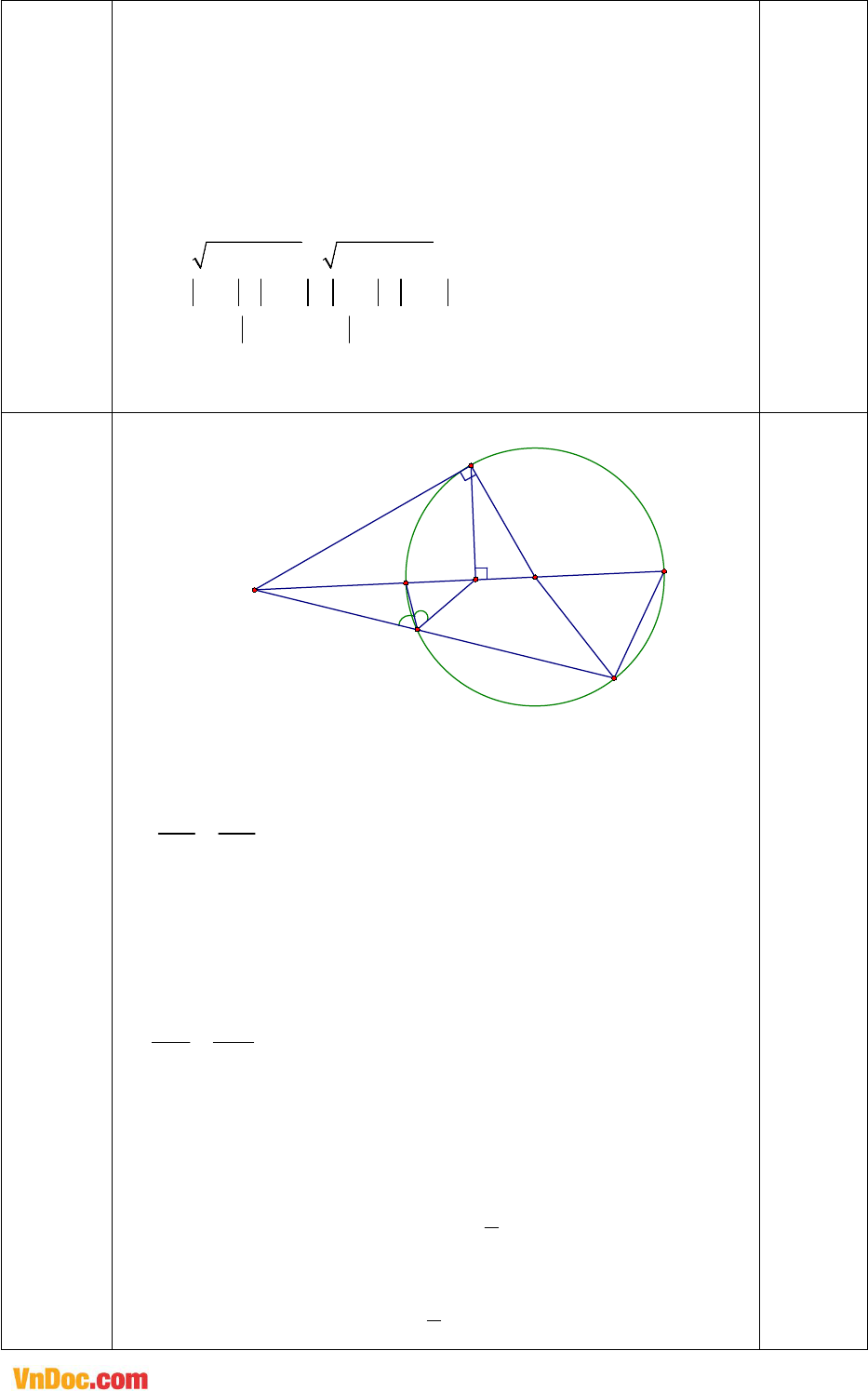
Đề thi giáo viên dạy giỏi môn Toán trường THCS Kim Liên năm 2018 - 2019 là đề thi đánh giá năng lực có đáp án chi tiết kèm theo, gồm 6 câu tự luận với thời gian làm bài 150 phút, đánh giá năng lực giúp quý thầy cô giáo chuẩn bị và ôn tập hiệu quả trước kì thi Giáo viên dạy giỏi THCS cấp trường. Mời các thầy cô tham khảo chi tiết.
Ngoài ra để chuẩn bị cho các kì thi giáo viên giỏi cấp trường, các thầy cô tham khảo chi tiết các tình huống sư phạm thường gặp và các đề thi giáo viên giỏi và các mẹo chuẩn bị cho các bài thi giáo viên dạy giỏi, thi công chức viên chức.
