Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

Đóng

Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm

Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169

VnDoc.com

Phân loại: Tài liệu Tính phí

Kẹo Ngọt Toán học lớp 7

Luyện tập 2 trang 53 Toán 7 tập 1 Kết nối tri thức

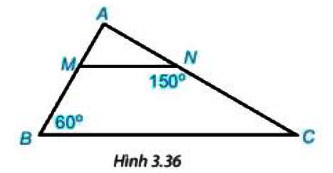
1) Cho hình 3.36. biết MN // BC, $\widehat {ABC} = {60^0};\widehat {MNC} = {150^0}$ . Hãy tính số đo các góc BMN và ACB.

Hình 3.36

2) Cho hình 3.37, biết rằng xx’ // yy’ và zz’ ⊥ xx’. Tính số đo góc ABy và cho biết zz’ có vuông góc với yy’ không.

2 3

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!

Xóa Đăng nhập để viết

3 Câu trả lời

Bé Heo
1) Ta có: MN // BC

=> (Hai góc nằm ở vị trí đồng vị)

Ta lại có: Góc AMN và góc NMB là hai góc kề bù.

=> $\widehat {AMN} + \widehat {NMB} = {180^0}$

=> $\widehat {NMB} = {180^0} - \widehat {AMN} = {180^0} - {60^0} = {120^0}$

Vậy $\widehat {NMB} = {120^0}$

Ta có: Góc ANM và góc MNC là hai góc kề bù.

=> $\widehat {ANM} + \widehat {MNC} = {180^0}$

=> $\widehat {ANM} = {180^0} - \widehat {MNC} = {180^0} - {150^0} = {30^0}$

Mà NM // BC

=> $\widehat {ANM} = \widehat {ACB} = {30^0}$ (Hai góc ở vị trí đồng vị)

Vậy $\widehat {ACB} = {30^0}$

2) Ta có: zz’ ⊥ xx’ => $\widehat {zAx'} = {90^0}$

Mà xx’ // yy’

=> $\widehat {zAx'} = \widehat {ABy'} = {90^0}$ (hai góc ở vị trí đồng vị)

=> zz’ ⊥ yy’

0 Trả lời 24/10/24
Bọ Cạp
Xem đáp án tại đây: Giải Toán 7 bài 10: Tiên đề Euclid. Tính chất của hai đường thẳng song song

0 Trả lời 24/10/24
Anh nhà tui
Thanks

0 Trả lời 24/10/24