Soạn Toán 8 bài 3 Những hằng đẳng thức đáng nhớ VNEN
Soạn Toán 8 VNEN bài 3 Những hằng đẳng thức đáng nhớ được VnDoc sưu tầm và đăng tải, hy vọng với tài liệu này các sẽ giúp ích cho các bạn học tốt môn Toán lớp 8. Mời các bạn tải về tham khảo chuẩn bị tốt cho bài học sắp tới của mình
Bài 3 Những hằng đẳng thức đáng nhớ VNEN
A. B. Hoạt động khởi động và hình thành kiến thức
a) Thực hiện các yêu cầu:
- Với a và b là hai số bất kì, tính (a + b)(a + b).
- Với a > 0; b > 0, hãy tính tích (a + b)(a + b) thông qua việc tính diện tích hình vuông ABCD theo hai cách.
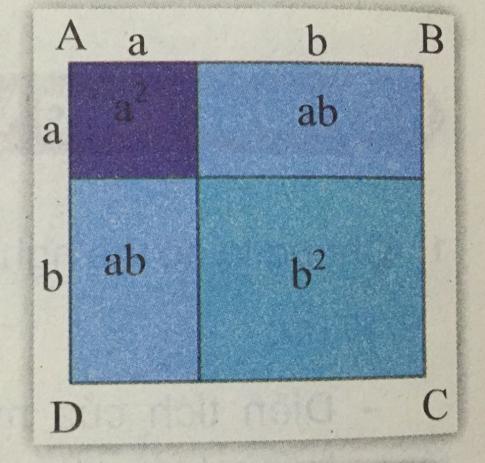
Trả lời:
- Với a, b là hai số bất kì, ta có:
\((a + b)(a + b) = a^{2} + ab + ba + b^{2} = a^{2} + 2ab + b^{2}.\)
- Với a > 0; b > 0, ta có thể tính diện tích ABCD theo hai cách như sau:
Cách 1: \(S_{ABCD} = (a + b)(a + b)\)
Cách 2: \(S_{ABCD} = a^{2} + ab + ba + b^{2} = a^{2} + 2ab + b^{2}\)
Như vậy, qua việc tính diện tích hình vuông ABCD theo hai cách như trên, ta có thể suy ra tích
\((a + b)(a + b) = a^{2} + ab + ba + b^{2} = a^{2} + 2ab + b^{2}.\)
b) Thực hiện các yêu cầu:
- Tính \((2b + 1)^{2}.\)
- Điền chữ, số thích hợp vào chỗ chấm để viết biểu thức \(x^{2} + 4x + 4\) dưới dạng bình phương của một tổng: \(x^{2} + 4x + 4 = x^{2} + 2.x.2 + 2^{2} =\) ……………………………..
- Tính nhanh \(401^{2}\).
Trả lời:
- Có: \((2b + 1)^{2} = (2b)^{2} + 2.2b.1 + 1^{2} = 4b^{2} + 4b + 1.\)
- Có: \(x^{2} + 4x + 4 = x^{2} + 2.x.2 + 2^{2} = …(x + 2)^{2} …\)
\(- 401^{2} = (400 + 1)^{2} = 400^{2} + 2.400.1 + 1^{2} = 160000 + 800 + 1 = 160801.\)
a) Với a, b là hai số bất kì, hãy điền vào chỗ chấm để tính \((a – b)^{2}\) theo hai cách:
Cách 1:\((a – b)^{2} = [a + (-b)]^{2} = a^{2} + 2.a.(-b) + (-b)^{2} =\) \(……………………;\)
Cách 2: \((a – b)(a – b) = ……………… = …………………\)
Trả lời:
Cách 1: \((a – b)^{2} = [a + (-b)]^{2} = a^{2} + 2.a.(-b) + (-b)^{2} = a^{2} - 2ab + b^{2};\)
Cách 2: \((a – b)(a – b) = a^{2} - ab - ba + b^{2} = a^{2} - 2ab + b^{2}.\)
b) Thực hiện các yêu cầu:
- Tính \((2x – y)^{2}\).
- Tính nhanh \(999^{2}\).
Trả lời:
- Có: \((2x – y)^{2} = (2x)^{2} - 2.2x.y + y^{2} = 4x^{2} - 4xy + y^{2}\).
- Có: \(999^{2} = (1000 – 1)^{2} = 1000^{2} - 2.1000.1 + 1^{2} = 1000000 – 2000 + 1 = 998001.\)
a)Với a, b bất kì, tính (a + b)(a – b).
Trả lời:
\((a + b)(a – b) = a^{2} - ab + ba - b^{2} = a^{2} - b^{2}.\)
b) Thực hiện các yêu cầu:
- Tính \((x – 2y)(x + 2y)\).
- Tính nhanh 77.83.
Trả lời:
- Có: \((x – 2y)(x + 2y) = x^{2} - (2y)^{2} = x^{2} - 4y^{2}.\)
- Có: \(77.83 = (80 – 3)(80 + 3) = 80^{2} - 3^{2} = 6400 – 9 = 6391.\)
C. Hoạt động luyện tập
Câu 1: Trang 12 toán VNEN 8 tập 1
Hãy phát biểu bằng lời các hằng đẳng thức: bình phương của một tổng, bình phương của một hiệu, hiệu hai bình phương.
Bài làm:
- Bình phương của một tổng bằng bình phương số thứ nhất cộng với hai lần tích của số thứ nhất với số thứ hai cộng với bình phương số thứ hai.
- Bình phương của một hiệu bằng bình phương số thứ nhất trừ đi hai lần tích của số thứ nhất với số thứ hai cộng với bình phương số thứ hai.
- Hiệu hai bình phương bằng tích của tổng hai số đó với hiệu của hai số đó.
Câu 2: Trang 12 toán VNEN 8 tập 1
Tính:
\(a) (3 + xy^{2})^{2};\)
\(b) (10 – 2m^{2}n)^{2};\)
\(c) (a - b^{2})(a + b^{2}).\)
Bài làm:
\(a) (3 + xy^{2})^{2}= 3^{2}+ 2.3.xy^{2}+ (xy^{2})^{2}= 9 + 6xy^{2}+ x^{2}y^{4};\)
\(b) (10 – 2m^{2}n)^{2}= 10^{2}- 2.10.2m^{2}n + (2m^{2}n)^{2} = 100 – 40m^{2}n + 4m^{4}n^{2};\)
\(c) (a - b^{2})(a + b^{2}) = a^{2}- (b^{2})^{2}= a^{2} - b^{4}.\)
Câu 3: Trang 12 toán VNEN 8 tập 1
Viết các biểu thức sau dưới dạng bình phương của một tổng hoặc một hiệu:
\(a) 4x^{2}+ 4xy + y^{2};\)
\(b) 9m^{2}+ n^{2} - 6mn;\)
\(c) 16a^{2}+ 25b^{2}+ 40ab;\)
\(d) x^{2} - x + \frac{1}{4}.\)
Bài làm:
\(a) 4x^{2}+ 4xy + y^{2}= (2x)^{2} + 2.2x.y + y^{2} = (2x + y)^{2};\)
\(b) 9m^{2}+ n^{2}- 6mn = (3m)^{2} + n^{2} - 2.3m.n = (3m – n)^{2};\)
\(c) 16a^{2}+ 25b^{2}+ 40ab = (4a)^{2} + (5b)^{2} + 2.4a.5b = (4a + 5b)^{2};\)
\(d) x^{2}- x +\frac{1}{4} = x^{2} - 2.x.\frac{1}{2} +(\frac{1}{2})^{2} = (x - \frac{1}{2})^{2}.\)
Câu 4: Trang 12 toán VNEN 8 tập 1
Hãy tìm cách giúp bạn Huy khôi phục lại những hằng đẳng thức bị mực làm nhòe đi một số chỗ:
\(a) x^{2}+ 6xy + …… = (…… + 3y)^{2};\)
\(b) (…… - ……)^{2}= a^{2} - …… + 4b^{4};\)
\(c) (…… + ……)^{2}= …… + m +\frac{1}{4}; d) …… - 4n^{4} = (m + ……)(m - ……).\)
Bài làm:
\(a) x^{2}+ 6xy + …9y^{2}… = (…x… + 3y)^{2};\)
\(b) (…a… - …2b…)^{2}= a^{2} - …4ab… + 4b^{4};\)
\(c) (…m… + …\frac{1}{2}m…)^{2}= …m^{2}… + m +\frac{1}{4};\)
\(d) …m^{2}… - 4n^{4} = (m + …2n^{2}…)(m - …2n^{2}…).\)
Câu 5: Trang 12 toán VNEN 8 tập 1
Tính nhanh:
\(a) 301^{2};\) \(b) 499^{2};\) \(c) 68.72.\)
Bài làm:
\(a) 301^{2}= (300 + 1)^{2}= 300^{2} + 2.300.1 + 1^{2} = 90000 + 600 + 1 = 90601;\)
\(b) 499^{2}= (500 – 1)^{2}= 500^{2} - 2.500.1 + 1^{2} = 250000 - 1000 + 1 = 249001;\)
\(c) 68.72 = (70 – 2)(70 + 2) = 70^{2}- 2^{2}= 4900 – 4 = 4896.\)
Câu 6: Trang 12 toán VNEN 8 tập 1
Bình viết: \(x^{2} - 12x + 36 = (x – 6)^{2}.\)
Minh viết: \(x^{2} - 12x + 36 = (6 – x)^{2}.\)
Hương nêu nhận xét: Minh viết sai, Bình viết đúng.
Sơn nói: Qua ví dụ trên, mình rút ra một hằng đẳng thức rất đẹp!
Hãy nêu ý kiến của em. Sơn rút ra được hằng đẳng thức nào?
Bài làm:
Trong trường hợp trên, nhận xét của hai bạn Hương và Sơn đều đúng.
Hằng đẳng thức ta rút ra được từ ví dụ trên là: \((A – B)^{2} = (B – A)^{2}.\)
Soạn Toán 8 bài 3 Những hằng đẳng thức đáng nhớ VNEN. Trên đây VnDoc đã hướng dẫn các bạn soạn Toán 8, lời giải chi tiết dễ hiểu hy vọng sẽ giúp các bạn củng cố thêm kiến thức từ đó vận dụng vào giải các các bài tập Toán lớp 8. Mời các bạn cùng tham khảo
.............................................
Ngoài Soạn Toán 8 bài 3 Những hằng đẳng thức đáng nhớ VNEN. Mời các bạn học sinh còn có thể tham khảo các Giải bài tập Toán lớp 8, Giải Vở BT Toán 8 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với tài liệu lớp 8 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn học tốt
