Công thức Toán cơ bản và nâng cao lớp 5
Công thức Toán cơ bản và nâng cao lớp 5
Công thức Toán cơ bản và nâng cao lớp 5 được VnDoc sưu tầm, tổng hợp trọn bộ công thức Toán tiểu học lớp 5 giúp các em học sinh hệ thống lại các công thức đã học vận dụng cho từng dạng bài tập. Đồng thời đây cũng là tài liệu hữu ích cho các thầy cô tổng hợp các kiến thức cần giảng dạy trong chương trình giảng dạy môn Toán tiểu học.
I/ Đại lượng tỉ lệ thuận và đại lượng tỉ lệ nghịch
Trong bài toán về đại lượng tỉ lệ thuận (hoặc tỉ lệ nghịch) thương xuất hiện hai đại lượng biến thiên theo tương quan tỉ lệ thuận (hoặc tỉ lệ nghịch). Trong hai đại lượng biến thiên này, người ta thường cho biết hai giá trị của đại lượng này và một giá trị của đại lượng kia rồi yêu cầu tìm giá trị còn lại của đại lượng thứ hai.
Để tìm giá trị này ta có thể dùng phương pháp rút về đơn vị hoặc phương pháp tỉ số.
+ Phương pháp rút về đơn vị:
Khi giải toán bằng phương pháp rút về đơn vị ta tiến hành theo các bước sau:
Bước 1: Rút về đơn vị: Trong bước này ta tính một đơn vị của đại lượng thứ nhất ứng với bao nhiêu đơn vị của đại lượng thứ hai hoặc ngược lại.
Bước 2: Tìm giá trị chưa biết của đại lượng thứ hai: Trong bước này lấy giá trị còn lại của đại lượng thứ nhất nhân với (hoặc chia cho) giá trị của đại lượng thứ hai tương ứng với một đơn vị của đại lượng thứ nhất (vừa tìm được ở bước 1)
+ Phương pháp tỉ số:
Khi giải toán bằng phương pháp tỉ số ta tiến hành theo các bước sau:
Bước 1: Tìm tỉ số: Ta xác định trong hai giá trị đã biết của đại lượng thứ nhất thì giá trị này gấp (hoặc kém) giá trị kia mấy lần.
Bước 2: Tìm giá trị chưa biết của đại lượng thứ hai.
a/ Đại lượng tỉ lệ thuận: Hai đại lượng gọi là tỉ lệ thuận với nhau khi đại lượng này tăng (hay giảm) bao nhiêu lần thì đại lượng kia cũng tăng (hay giảm) bấy nhiêu lần.
Muốn giải loại toán này ta cần phải thực hiện qua hai bước:
Bước 1: Xác định hai đại lượng tỉ lệ thuận với nhau.
Bước 2: Dùng phương pháp rút về đơn vị hoặc phương pháp dùng tỉ số để giải bài toán.
Ví dụ 1: May 5 bộ quần áo như nhau hết 20m vải. Hỏi may 23 bộ quần áo như thế thì hết bao nhiêu mét vải cùng loại ?
Phân tích:
Trong bài toán này xuất hiện ba đại lượng:
- Số mét vải để may 1 bộ quần áo là đại lượng không đổi.
- Số bộ quần áo và số mét vải là hai đại lượng biến thiên theo tương quan tỉ lệ thuận.
Ta thấy:
May 5 bộ quần áo hết 20m vải.
May một bộ quần áo hết ?m vải.
May 23 bộ quần áo hết ?m vải.
Lời giải
Số mét vải may 1 bộ quần áo là:
20: 5 = 4 (m)
Số mét vải để may 23 bộ quần áo là:
4 x 23 = 92 (m)
Đáp số: 92m vải
Ví dụ 1: chỉ giải được bằng phương pháp rút về đơn vị (vì tỉ số 23: 5 không phải là số tự nhiên).
Ví dụ 2: Lát 9m2 nền nhà hết 100 viên gạch. Hỏi lát 36m2 nền nhà cùng loại gạch đó thì hết bao nhiêu viên ?
Phân tích:
Trong bài toán này xuất hiện ba đại lượng:
- Một đại lượng không đổi là số viên gạch để lát 1m2 nền nhà.
Ta thấy diện tích 36m2 gấp 4 lần diện tích 9m2, vì vậy số gạch cần để lát 36m2 gấp 4 lần số gạch để lát 9m2.
- Hai đại lượng biến thiên theo tương quan tỉ lệ thuận là số viên gạch và diện tích nền nhà.
Lời giải
Diện tích 36m2 gấp diện tích 9m2 số lần là:
36: 9 = 4 (lần)
Số gạch để cần lát 36m2 nên nhà là:
100 x 4 = 400 (viên)
II/ Tỉ số phần trăm
1/ Tìm tỉ số phần trăm của hai số:
Muốn tìm tỉ số phần trăm của hai số ta làm như sau:
- Tìm thương của hai số đó.
- Nhân thương đó với 100 và viết thêm kí hiệu % vào bên phải tích tìm được.
Ví dụ: Trong 80kg nước biển có 2,8kg muối. Tìm tỉ số phần trăm của lượng muối trong nước biến.
Giải: Tỉ số phần trăm của lượng muối trong nước biến là:
2,8 : 80 = 0,035 = 3,5%
Đáp số: 3,5%
2/ Tìm giá trị tỉ số phần trăm của một số:
Muốn tìm giá trị tỉ số phần trăm của một số ta đem số đó nhân với số phần trăm.
Ví dụ: Một trường tiểu học có 800 học sinh, trong đó số học sinh nữ chiếm 52%. Tính số học sinh nữ của trường đó.
Phân tích: Tìm số học sinh nữ có nghĩa là tìm giá trị 52% của 800.
Giải: Số học sinh nữ của trường đó là:
![]() \(\frac{800\times52}{100}\)= 416 (học sinh)
\(\frac{800\times52}{100}\)= 416 (học sinh)
Đáp số: 16 học sinh.
3/ Tìm một số khi biết giá trị một số phần trăm của nó
Muốn tìm một số khi biết giá trị một số phần trăm của nó, ta đem giá trị ấy chia cho số phần trăm.
Ví dụ: Số học sinh nữ của trường là 416 em và chiếm 52% số học sinh toàn trường. Hỏi trường đó có bao nhiêu học sinh ?
Phân tích: Tìm số học sinh toàn trường có nghĩa là tìm một số khi biết số học sinh nữ là 52%.
Giải: Số học sinh của trường đó là:
![]() \(416:\frac{52}{100}=800\) (học sinh)
\(416:\frac{52}{100}=800\) (học sinh)
III/ Công thức hình học
1. Hình tam giác
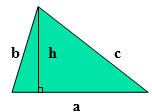
1 Kiến thức cần nhớ.
Công thức tính :
a/ Chu vi hình tam giác:
Muốn tìm chu vi hình tam giác ta lấy ba cạnh cộng lại.
P = a + b + c
b/ Diện tích hình tam giác :
Muốn tìm diện tích hình tam giác ta lấy đáy nhân với chiều cao rồi chia cho 2.
![]() \(S=\frac{a\times h}{2}\)
\(S=\frac{a\times h}{2}\)
c/ Đáy hình tam giác :
Muốn tìm đáy hình tam giác ta lấy hai lần diện tích chia cho chiều cao.
![]() \(a=\frac{S\times2}{h}\)
\(a=\frac{S\times2}{h}\)
c/ Chiều cao hình tam giác :
Muốn tìm chiều cao hình tam giác ta lấy hai lần diện tích chia cho đáy.
![]() \(h=\frac{S\times2}{a}\)
\(h=\frac{S\times2}{a}\)
Các em học sinh tham khảo chi tiết tại file tải về.
Công thức Toán cơ bản và nâng cao lớp 5 bao gồm các công thức Số học và Hình học cho các em học sinh tham khảo tổng hợp lại các dạng kiến thức môn Toán lớp 5 chuẩn bị cho các kì thi học kì, thi học sinh giỏi, thi lên lớp 6 chi tiết.











