Đề thi Olympic môn Toán lớp 11 trường THPT Đa Phúc, Hà Nội năm học 2016 - 2017
Đề thi Olympic môn Toán lớp 11
Đề thi Olympic môn Toán lớp 11 trường THPT Đa Phúc, Hà Nội năm học 2016 - 2017 được VnDoc.com sưu tầm và đăng tải, giúp các em làm quen với cấu trúc đề, biết các nội dung, kiến thức chủ yếu mà đề thi học sinh giỏi hay ra. Từ đó biết cách ôn tập và làm đề thi để đạt kết quả tốt nhất. Chúc các em thành công.
Đề thi học sinh giỏi môn Toán lớp 11 trường THPT Tam Quan năm 2015 - 2016
Đề thi học sinh giỏi môn Toán lớp 11 trường THPT Gia Viễn B, Ninh Bình năm học 2015 - 2016
|
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI |
ĐỀ THI OLYMPIC NĂM HỌC 2016 - 2017 |
|
TRƯỜNG THPT ĐA PHÚC |
MÔN: TOÁN – LỚP: 11 Thời gian làm bài: 120 phút |
Câu 1. (4,0 điểm)
1. Tìm m để phương trình sau có đúng 2 nghiệm thuộc [0; π]
(2sinx - 1)(2cos2x + 2sinx + m) = 1 - 2cos2x (Với m là tham số)
2. Chứng minh tam giác ABC thỏa mãn: sinA + sinB + sinC = 1 + cosA + cosB + cosC thì tam giác ABC vuông.
Câu 2. (2,0 điểm) Tính giá trị biểu thức:
![]()
Câu 3. (4,0 điểm) Chứng minh rằng dãy số sau tăng và bị chặn trên
![]() (n dấu căn)
(n dấu căn)
Câu 4. (4,0 điểm)
Tìm giới hạn dãy số (nn) xác định như sau: 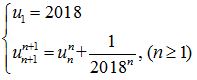
Câu 5. (6,0 điểm)
Cho tứ diện ABCD. Một mặt phẳng (α) song song với AC và BD cắt tứ diện theo thiết diện là tứ giác PQRS.
- Chứng minh rằng PQRS là hình bình hành.
- Xác định mặt phẳng (α) để PQRS là hình thoi.
- Xác định mặt phẳng (α) để PQRS có diện tích lớn nhất.
- - - - - - - - - - - -- Hết - - - - - - - - - - -- - - -
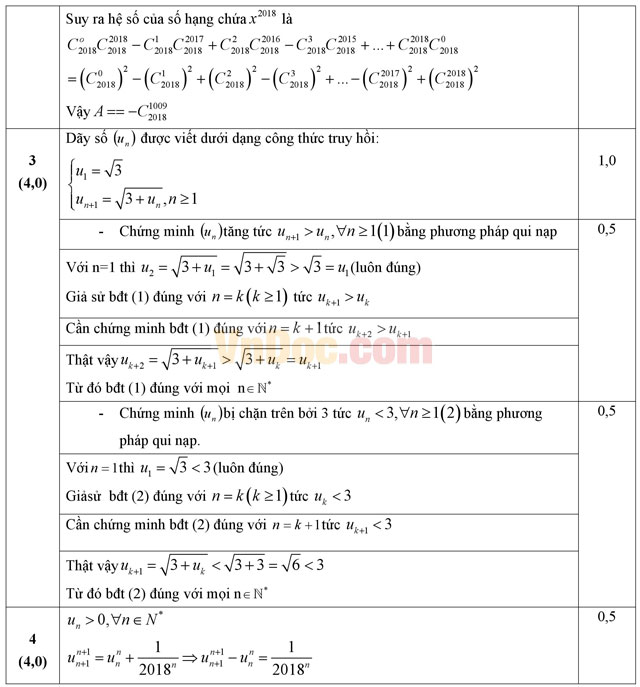
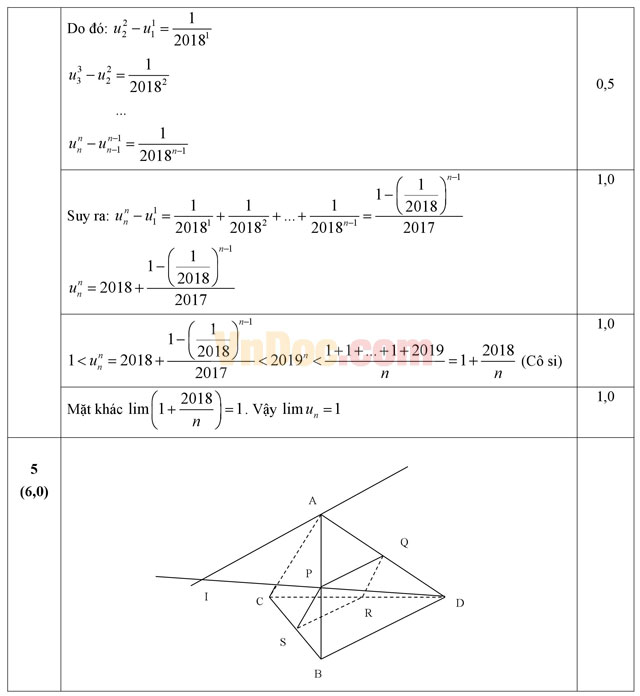
Đáp án đề thi Olympic môn Toán lớp 11