Đề thi tuyển sinh lớp 10 tỉnh Long An năm học 2011 - 2012 môn Toán tin (Hệ chuyên)

Vndoc.com xin giới thiệu đến các bạn lớp 9, chuẩn bị thi lên lớp 10: Đề thi tuyển sinh lớp 10 tỉnh Long An năm học 2011 - 2012 môn Toán tin (Hệ chuyên).

Đề thi tuyển sinh lớp 10 môn Toán tin:

SỞ GIÁO DỤC VÀ ĐÀO TẠO LONG AN (Đề thi chính thức)

KỲ THI TUYỂN SINH VÀO LỚP 10 HỆ CHUYÊN NĂM HỌC 2O11 – 2012 Môn thi: TOÁN TIN (Chuyên) (Thời gian làm bài 150 phút không kể thời gian giao đề) Ngày thi: 30/06/2011

Câu I: (1.5 điểm)

Rút gọn biểu thức:

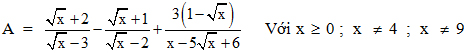
Câu II: (2 điểm)

Cho parabol (P): y = x² và đường thẳng (d): y = 2mx - m + 1

a. Chứng minh rằng: Đường thẳng (d) luôn cắt parabol (P) tại hai điểm phân biệt với mọi giá trị của m

b. Gọi A (xA ; yA) và B (xB ; yB ) là hai giao điểm phân biệt của (d) và (P)

Tìm giá trị lớn nhất của biểu thức:

Câu III: (1 điểm)

Giải hệ phương trình: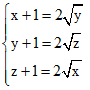


Câu IV: (2,5 điểm)

Từ một điểm M nằm bên ngoài đường tròn (O), vẽ hai tiếp tuyến MA, MB với đường tròn (O). (A và B là hai tiếp điểm). Cát tuyến qua M cắt (O) tại C và D (C nằm giữa M và D). Gọi H là giao điểm của OM và AB

a) Chứng minh: MC.MD = MA²

b) Chứng minh: Tứ giác HCDO nội tiếp.

c) Chứng minh: HA là tia phân giác của góc CHD

Câu V: (1 điểm)

Giải phương trình nghiệm nguyên: x² + xy – y = 0

Câu VI: (1 điểm)

Người ta đặt tùy ý 10 điểm vào trong một tam giác đều có cạnh bằng 3 (Kể cả trên các cạnh của tam giác). Chứng minh rằng: Ta luôn tìm được hai điểm mà khoảng cách giữa chúng không vượt quá 1

Câu VII: ( 1 điểm)

Cho hai số nguyên x , y thỏa mãn: x² + y² chia hết cho 3

Chứng minh rằng: xy chia hết cho 9