Giải SBT Toán 6 Bài 5: Phép tính lũy thừa với số mũ tự nhiên

Giải SBT Toán 6 Bài 5: Phép tính lũy thừa với số mũ tự nhiên có đáp án chi tiết. Các em học sinh có thể tham khảo đối chiếu với bài của mình đã làm. Các lời giải dưới đây các em luyện giải bài tập tại nhà mà không cần sách giải.

>> Bài trước: Giải SBT Toán 6 Bài 4: Phép nhân, phép chia số tự nhiên

Bài 37 trang 17 SBT Toán 6 tập 1

a) Viết mỗi số sau thành bình phương của một số tự nhiên:

36; 64; 169; 225; 361; 10 000.

b) Viết mỗi số sau thành lập phương của một số tự nhiên:

8; 27; 125; 216; 343; 8 000.

Đáp án

a) Ta có:

36 = 6.6 = 6²;

64 = 8.8 = 8²;

169 = 13.13 = 13²;

225 = 15.15 = 15²;

361 = 19.19 = 19²;

10 000 = 100.100 = 100².

b) Ta có:

8 = 2.2.2 = 2³;

27 = 3.3.3 = 3³;

125 = 5.5.5 = 5³;

216 = 6.6.6 = 6³;

343 = 7.7.7 = 7³;

8 000 = 20.20.20 = 20³.

Bài 38 trang 17 SBT Toán 6 tập 1

Cho các số 16; 20; 25; 60; 81; 90; 1 000; 1 331. Trong các số đó, số nào viết được dưới dạng lũy thừa của một số tự nhiên với số mũ lớn hơn 1? (Chú ý rằng có những số có nhiều cách viết dưới dạng lũy thừa)

Đáp án

Các số viết được dưới dạng lũy thừa của một số tự nhiên với số mũ lớn hơn 1 là: 16; 25; 81; 1 000; 1 331. Trong đó:

+) 16 = 4.4 = 4² hoặc 16 = 2.2.2.2 = 2⁴;

+) 25 = 5.5 = 5²;

+) 81 = 9.9 = 9² hoặc 81 = 3.3.3.3 = 3⁴;

+) 1 000 = 10.10.10 = 10³;

+) 1 331 = 11.11.11 = 11³.

Bài 39 trang 17 SBT Toán 6 tập 1

Viết kết quả của mỗi phép tính sau dưới dạng một lũy thừa, một tích các lũy thừa hoặc một tổng các lũy thừa:

a) 3.3.3.3.3;

b) y.y.y.y;

c) 5.p.5.p.2.q.4.q;

d) a.a + b.b + c.c.c + d.d.d.d.

Đáp án

a) 3.3.3.3.3 = 3⁵;

b) y.y.y.y = y⁴;

c) 5.p.5.p.2.q.4.q = (5.5)(2.4).(p.p).(q.q) = 5².(2.2.2).p².q² = 5².2³.p².q².

d) a.a + b.b + c.c.c + d.d.d.d = a² + b² + c³ + d⁴.

Bài 40 trang 17 SBT Toán 6 tập 1

Tế bào lớn lên đến một kích thước nhất định thì phân chia. Quá trình đó diễn ra như sau: Đầu tiên từ 1 nhân thành 2 nhân tách xa nhau. Sau đó chất tế bào được phân chia, xuất hiện một vách ngăn, ngăn đôi tế bào cũ thành 2 tế bào con. Các tế bào con tiếp tục lớn lên cho đến khi bằng tế bào mẹ. Các tế bào này tiếp tục phân chia thành 4, rồi thành 8, … tế bào.

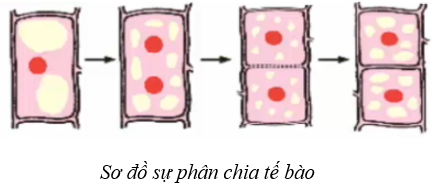
Như vậy từ một tế bào mẹ: sau khi phân chia lần 1 được hai tế bào con; lần hai được 2² = 4 (tế bào con); lần ba được 2³ = 8 (tế bào con). Hãy tính số tế bào con có được ở lần phân chia thứ 5, thứ 8 và thứ 11.

Đáp án

Theo quy luật phân chia tế bào, ta có:

Lần 1: 2¹ = 2 (tế bào con);

Lần 2: 2² = 4 (tế bào con);

Lần 3: 2³ = 4 (tế nào con);

…

Vậy lần thứ n được: 2ⁿ (tế bào con).

Số tế bào con có được ở lần phân chia thứ 5 là: 2⁵ = 32 (tế bào con).

Số tế bào con có được ở lần phân chia thứ 8 là: 2⁸ = 256 (tế bào con).

Số tế bào con có được ở lần phân chia thứ 11 là: 2¹¹ = 2 048 (tế bào con).

Bài 41 trang 17 SBT Toán 6 tập 1

Một nền nhà có dạng hình vuông gồm a hàng, mỗi hàng lát a viên gạch. Ban An đếm được 113 viên gạch được lát trên nền nhà đó. Theo em bạn An đếm đúng hay sai? Vì sao?

Đáp án

Số viên gạch lát nền nhà đó là: a.a = a² (viên).

Do đó số viên gạch phải là bình phương của một số tự nhiên hay a là số chính phương. Số chính phương là các số có chữ số tận cùng là 0; 1; 4; 5; 6; 9.

Bạn An đếm được 113 viên gạch được lát nền nhà. Mà 113 không phải là số chính phương nên bạn An đã đếm sai.

Bài 42 trang 17 SBT Toán 6 tập 1

So sánh:

a) 2⁶ và 6²;

b) 7³⁺¹ và 7³ + 1;

c) 13¹⁴ – 13¹³ và 13¹⁵ – 13¹⁴;

d) 3²⁺ⁿ và 2³⁺ⁿ.

Đáp án

a) Ta có: 2⁶ = 2.2.2.2.2.2 = 8.8 = 8²;

Vì 8 > 6 nên 8² > 6² hay 2⁶ > 6².

Vậy 2⁶ > 6².

b) Ta có: 7³⁺¹ = 7³.7 = 7³ + 7³ + 7³ + 7³ + 7³ + 7³ + 7³ > 7³ + 1.

Vậy 7³⁺¹ > 7³ + 1.

c) Ta có: 13¹⁴ – 13¹³ = 13¹³.(13 – 1) = 13¹³.12.

13¹⁵ – 13¹⁴ = 13¹⁴.(13 – 1) = 13¹⁴.12.

Vì 14 > 13 nên 13¹⁴ > 13¹³. Do đó 13¹⁴.12 > 13¹³.12 hay 13¹⁵ – 13¹⁴ > 13¹⁴ – 13¹³.

Vậy 13¹⁵ – 13¹⁴ > 13¹⁴ – 13¹³.

d) 3²⁺ⁿ và 2³⁺ⁿ.

Ta có: 3²⁺ⁿ = 3².3ⁿ = 9.3ⁿ;

2^{3 + n} = 2³.2ⁿ = 8.2ⁿ.

Vì 3 > 2 nên 3ⁿ > 2ⁿ và 9 > 3 do đó 9.3ⁿ > 8.2ⁿ hay 3²⁺ⁿ > 2³⁺ⁿ.

Vậy 3²⁺ⁿ > 2³⁺ⁿ.

Bài 43 trang 18 SBT Toán 6 tập 1

Rút gọn biểu thức sau:

a) A = 1 + 3 + 32 + 33 + … + 399 + 3100;

b) B = 2100 – 299 + 298 – 297 + … - 23 + 22 – 2 + 1.

Đáp án

a) A = 1 + 3 + 32 + 33 + … + 399 + 3100;

Ta có 3A = 3 + 32 + 33 + … + 399 + 3100 + 3101

Khi đó: 3A – A = 3 + 32 + 33 + … + 399 + 3100 + 3101 – (1 + 3 + 32 + 33 + … + 399 + 3100)

= 3101 – 1.

Suy ra: 2A = 3101 – 1

A = (3101 – 1):2.

Vậy A = (3101 – 1):2.

b) B = 2100 – 299 + 298 – 297 + … - 23 + 22 – 2 + 1

Ta có: 2B = 2101 – 2100 + 299 – 298 + … 23 – 22 + 2.

Khi đó 2B + B = (2101 – 2100 + 299 – 298 + … 23 – 22 + 2) + (2100 – 299 + 298 – 297 + … - 23 + 22 – 2 + 1) = 2101 + 1

3B = 2101 + 1

Suy ra: B = (2101 + 1):3.

Vậy B = (2101 + 1):3.

Bài 44 trang 18 SBT Toán 6 tập 1

Viết kết quả của mỗi phép tính sau dưới dạng một lũy thừa:

a) 7⁴.7⁵.7⁶;

b) (54 : 3)⁷.324;

c) [(8 + 2)².10¹⁰⁰] : (10⁰.10⁹⁴);

d) a⁹:a⁹ (a 0).

Đáp án

a) 7⁴.7⁵.7⁶ = 7^{4 + 5 + 6} = 7¹⁵;

b) (54:3)⁷:324 = 18⁷.324 = 18⁷.18.18 = 18^{7 + 1 + 1} = 18⁹;

c) [(8 + 2)².10¹⁰⁰] : (10⁰.10⁹⁴)

= [10².10¹⁰⁰]:(10⁹⁴)

= 10^{2 + 100}:10⁹⁴

= 10¹⁰²:10⁹⁴

= 10^{102 – 94}

= 10⁸.

d) a⁹:a⁹ (a 0)

= a^{9 – 9}

= a⁰.

Bài 45 trang 18 SBT Toán 6 tập 1

a) Viết các số: 123 ; 2 355 ; \(\overline {abcde}\) dưới dạng tổng các lũy thừa của 10.

b) Tìm số \(\overline {abcdef}\) (d \(\ne\) 0) sao cho \(\overline {abcdef} =999. \overline {abc} + 200\).

Đáp án

a) Ta có:

+ 123 = 1.100 + 2.10+3.1 = 1.102 +2. 101 +3.100

+ 2 355 = 2.1 000+ 3. 100 +5.10 +5.1 = 2. 103 + 3. 102 +5. 101 + 5. 100

+\(\overline {abcde}\) = a. 10 000 + b. 1 000+ c. 100+ d. 10+ e. 1 = a. 104 + b. 103 +c. 102+ d. 101 + e. 1

b) Ta có: \(\overline {abcdef} = 1 000. \overline {abc} +\overline {def}\)

Vì\(\overline {abcdef} =999. \overline {abc} + 200\) nên \(1 000. \overline {abc} +\overline {def} = 999. \overline {abc} + 200\)

Nên \(\overline {abc} + \overline {def} = 200\)(1)

Vì \(\overline {abc} , \overline {def}\) đều phải lớn hơn hoặc bằng 100 nên\(\overline {abc} + \overline {def}\) phải lớn hơn hoặc bằng 200(2)

Từ (1) và (2) suy ra\(\overline {abc} = \overline {def} = 100\)

Vậy số \(\overline {abcdef}\) là 100100.

Bài 46 trang 18 SBT Toán 6 tập 1

Tìm số tự nhiên x, biết:

a) 2^x + 12 = 44;

b) 2.5^x+1 – 1.100 = 6.5²;

c) 2.3^x+1 = 10.3¹² + 8.3¹²;

d) 2^x + 2^x+3 = 144.

Đáp án

a) 2^x + 12 = 44;

2^x = 44 – 12

2^x = 32

2^x = 2⁵

x = 5.

Vậy x = 5.

b) 2.5^x+1 – 1 100 = 6.5²

2.5^x+1 = 6.5² + 1 100

2.5^x+1 = 6.25 + 1 100

2.5^x+1 = 150 + 1 100

2.5^x+1 = 1 150

5^x+1 = 1 150:2

5^x+1 = 625

5^x+1 = 5⁴

x + 1 = 4

x = 4 – 1

x = 3.

Vậy x = 3.

c) 2.3^x+1 = 10.3¹² + 8.3¹²

2.3^x+1 = 3¹².(10 + 8)

2.3^x+1 = 3¹².18

3^x+1 = 3¹².18:2

3^x+1 = 3¹².9

3^x+1 = 3¹².3²

3^x+1 = 3¹⁴

x + 1 = 14

x = 13.

Vậy x = 13.

d) 2^x + 2^x+3 = 144.

2^x + 2^x.2³ = 144

2^x(1 + 2³) = 144

2^x.(1 + 8) = 144

2^x.9 = 144

2^x = 144:9

2^x = 16

2^x = 2⁴

x = 4.

Vậy x = 4.

Bài 47 trang 18 SBT Toán 6 tập 1

So sánh:

a) 2²⁰⁰ .2¹⁰⁰ và 3¹⁰⁰.3¹⁰⁰;

b) 21¹⁵ và 27⁵.49⁸;

c) 3³⁹ và 11².

Đáp án

a) Ta có nhận xét sau: (a^m)ⁿ = a^m.a^m…a^m (n thừa số a^m) = a^{m + m + …+m} = a^m.n.

Ta có:

2²⁰⁰ .2¹⁰⁰ = 2^{200 + 100} = 2³⁰⁰ = 2^3.100 = (2³)¹⁰⁰ = 8¹⁰⁰

3¹⁰⁰.3¹⁰⁰ = 3^{100 + 100} = 3²⁰⁰ = (3²)¹⁰⁰ = 9¹⁰⁰.

Vì 8 < 9 nên 8¹⁰⁰ < 9¹⁰⁰ hay 2²⁰⁰.2¹⁰⁰ < 3¹⁰⁰.3¹⁰⁰.

Vậy 2²⁰⁰.2¹⁰⁰ < 3¹⁰⁰.3¹⁰⁰.

b) Ta có nhận xét sau: (ab)^m = (ab).(ab).(ab)…(ab) = (a.a…a).(b.b…b) = a^m.b^m.

Khi đó:

21¹⁵ = (7.3)¹⁵ = 7¹⁵.3¹⁵

27⁵.49⁸ = (3³)⁵.(7²)⁸ = 3¹⁵.7¹⁶ = 3¹⁵.7¹⁵.7.

Vì 7¹⁵.3¹⁵ < 3¹⁵.7¹⁵.7 nên 21¹⁵ < 27⁵.49⁸.

Vậy 21¹⁵ < 27⁵.49⁸.

Bài 48 trang 18 SBT Toán 6 tập 1

Tìm chữ số tận cùng của kết quả mỗi phép tính sau:

a) 54¹⁰;

b) 49¹⁵;

c) 11²⁰ + 119²¹ + 2 000²²;

d) 138³³ – 2 020¹⁴.

Đáp án

a) Ta có: 54¹⁰ = (54²)⁵ = (2 916)⁵.

Tích của 5 chữ số 6 có chữ số tận cùng là 6 nên (2 916)⁵ có chữ số tận cùng là 6.

Vậy 54¹⁰ có chữ số tận cùng là 6.

b) 49¹⁵ = 49¹⁴.49 = (49²)⁷.49 = (2 401)⁷.49

Vì (2 401)⁷ có chữ số tận cùng là 1 nên (2 401)⁷.49 có chữ số tận cùng là 9.

Vậy chữ số tận cùng của số 49¹⁵ là 9.

c) Ta có 11²⁰ có chữ số tận cùng là 1;

119²¹ có chữ số tận cùng là 9;

2 000²² có chữ số tận cùng là 0.

Khi đó 11²⁰ + 119²¹ + 2 000²² có chữ số tận cùng là chữ số tận cùng của tổng 1 + 9 + 0 =10.

Vậy 11²⁰ + 119²¹ + 2 000²² có chữ số tận cùng là 0.

d) 138³³ = 138³².138 = (138⁴)⁸.138.

Vì (138⁴)⁸ có chữ số tận cùng là 6 nên (138⁴)⁸.138 có tận cùng là 8.

Mà 2 020¹⁴ có chữ số tận cùng là 0.

Do đó 138³³ – 2 020¹⁴ có chữ số tận cùng là 8.

Vậy chữ số tận cùng của 138³³ – 2 020¹⁴ là 8.

Bài 49 trang 18 SBT Toán 6 tập 1

a) Cho A = 4 + 2² + 2³ + … +2²⁰⁰⁵. Chứng tỏ rằng A là một lũy thừa cơ số 2.

b) Cho B = 5 + 5² + 5³ + … + 5²⁰²¹.

Đáp án

a) Ta có:

A = 2² + 2³ + … +2²⁰⁰⁵

A – 4 = 2² + 2³ + … +2²⁰⁰⁵

2(A – 4) = 2³ + 2⁴ + … + 2²⁰⁰⁶

2(A – 4) – (A – 4) = (2³ + 2⁴ + … + 2²⁰⁰⁶) – (2² + 2³ + … +2²⁰⁰⁵) = 2²⁰⁰⁶ – 2²

A – 4 = 2²⁰⁰⁶ – 4

A = 2²⁰⁰⁶.

Vậy A là một lũy thừa bậc 2006 cơ số 2.

b) B = 5 + 5² + 5³ + … + 5²⁰²¹

Ta thấy các lũy thừa cơ số 5 là một số có chữ số tận cùng là 5 mà B có 2021 số hang là lũy thừa của cơ số 5 nên chữ số tận cùng của B là 5. Suy ra B + 8 có kết quả là một số có chữ số tận cùng là 3 nên B + 8 không thể là bình phương của một số tự nhiên (vì không có bình phương số tự nhiên nào có chữ số tận cùng là 3).

>> Bài tiếp theo: Giải SBT Toán 6 Bài 6: Thứ tự thực hiện các phép tính

Thông qua lời giải Toán trên các em học sinh có thể luyện tập các dạng Toán trong chuyên mục Toán lớp 6 Cánh Diều phù hợp với nội dung chương trình mình đang học.

Các em học sinh tham khảo thêm Toán lớp 6 Kết nối tri thức và Toán lớp 6 Chân Trời Sáng Tạo. VnDoc liên tục cập nhật lời giải cũng như đáp án sách mới của SGK cũng như SBT các môn cho các bạn cùng tham khảo.