Bài toán giải bằng phân tích cấu tạo số
Bài toán giải bằng phân tích cấu tạo số
Các bài toán vận dụng kiến thức về cấu tạo số là các bài toán yêu cầu học sinh phải biết suy luận logic và phải có kiến thức tổng hợp cao. Và quan trọng học sinh phải nắm vững kiến thức và qui luật về cấu tạo số. Mời quý thầy cô và các em học sinh cùng tham khảo các bài toán giải bằng phân tích câu tạo số sau đây, nhằm có phương pháp thích hợp khi giải các bài toán dạng này.
Lưu ý: Để tham khảo toàn bộ bài viết, các bạn tải về chi tiết link tải bên dưới.
Loại 1: Viết thêm một số chữ số vào bên trái, bên phải hoặc xen giữa các chữ số của một số tự nhiên
Ví dụ 1: Tìm một số tự nhiên có hai chữ số biết rằng khi viết thêm số 12 vào bên trái số đó ta được số mới lớn gấp 26 lần số phải tìm.
Bài giải
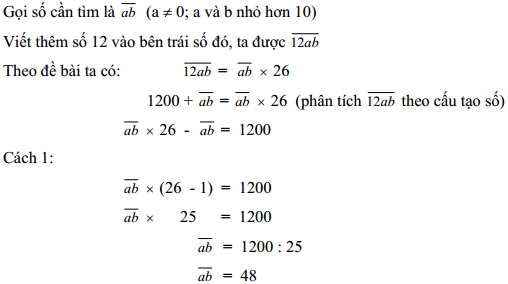
Thử lại: 1248 : 48 = 26
Cách 2: Ta có sơ đồ sau:
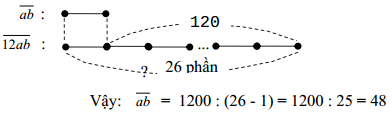
Thử lại: 1248 : 26 = 48
Ví dụ 2: Tìm một số tự nhiên có ba chữ số biết rằng khi viết thêm chữ số 2 vào bên phải số đó thì nó tăng thêm 4106 đơn vị.
Bài giải
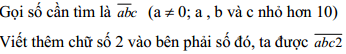
Thử lại: 4562 - 456 = 4106
Cách 2: Khi viết thêm chữ số 2 vào bên phải một số tự nhiên thì số đó gấp lên 10 lần và 2 đơn vị.
Ta có sơ đồ sau:
Vậy số cần tìm là: (4106 - 2) : (10 - 1) = 456
Thử lại: 4562 - 456 = 4106
Ví dụ 3: Tìm một số tự nhiên có hai chữ số biết rằng khi viết thêm chữ số 0 xen giữa chữ số hàng chục và hàng đơn vị của số đó, ta được số lớn gấp 10 lần số cần tìm, nếu viết thêm chữ số 1 vào bên trái số vừa nhận được thì số đó lại tăng thêm 3 lần.
Bài giải
Gọi số cần tìm là 
\(\overline{\mathrm{ab}}\) (a ≠ 0; a và b nhỏ hơn 10)
Viết thêm chữ số 0 vào giữa chữ số hàng chục và hàng đơn vị của số đó, ta được \(\overline{\mathrm{a0b}}\)
Theo đề bài ta có: \(\overline{\mathrm{ab}}\) × 10 = \(\overline{\mathrm{a0b}}\) .
Vì \(\overline{\mathrm{ab}}\) × 10 có tận cùng bằng 0 nên b = 0.
Vậy số cần tìm có dạng\(\overline{\mathrm{a00}}\) .
Viết thêm chữ số 1 vào bên trái \(\overline{\mathrm{a00}}\) ta được \(\overline{\mathrm{1a00}}\).
Theo đề bài ta lại có:
\(\overline{\mathrm{1a00}}\) = 3 × \(\overline{\mathrm{a00}}\)
1000 + a 100 = 3 × a × 100
1000 + a × 100 = a × 300
a × 300 - a × 100 = 1000
a × (300 - 100) = 1000
a × 200 = 1000
a = 1000 : 200
a = 5
Vậy số cần tìm là 50.
Thử lại: 500 : 10 = 50
Loại 2: Xóa đi một số chữ số của một số tự nhiên
Ví dụ 4: Tìm số tự nhiên có 4 chữ số. Biết rằng nếu ta xóa đi chữ số hàng chục và hàng đơn vị thì số đó giảm đi 4455 đơn vị.
Bài giải
Gọi số cần tìm là \(\overline{\mathrm{abcd}}\) (a ≠ 0; a , b, c và d nhỏ hơn 10)
Xóa đi chữ số hàng chục và hàng đơn vị của số đó, ta được \(\overline{\mathrm{ab}}\)
Theo đề bài ta có: \(\overline{\mathrm{abcd}}\) - \(\overline{\mathrm{ab}}\) = 4455
\(\overline{\mathrm{ab}}\) × 100 + \(\overline{\mathrm{cd}}\) - \(\overline{\mathrm{ab}}\)= 4455 (phân tích \(\overline{\mathrm{abcd}}\) theo cấu tạo số)
\(\overline{\mathrm{cd}}\)+ \(\overline{\mathrm{ab}}\) × 100 - \(\overline{\mathrm{ab}}\)= 4455
\(\overline{\mathrm{cd}}\)+ \(\overline{\mathrm{ab}}\) × (100 - 1) = 4455
\(\overline{\mathrm{cd}}\)+ \(\overline{\mathrm{ab}}\) × 99 = 45 × 99 (phân tích 4455 = 45 × 99)
\(\overline{\mathrm{cd}}\)= 99 × (45 - \(\overline{\mathrm{ab}}\))
Ta nhận thấy tích của 99 và một số tự nhiên là một số tự nhiên bé hơn 100 nên 45 - \(\overline{\mathrm{ab}}\)phải bằng 0 hoặc 1.
- Nếu 45 - \(\overline{\mathrm{ab}}\)= 0 thì \(\overline{\mathrm{ab}}\)= 45 và \(\overline{\mathrm{cd}}\)= 00
- Nếu 45 - \(\overline{\mathrm{ab}}\) = 1 thì \(\overline{\mathrm{ab}}\) = 44 và \(\overline{\mathrm{cd}}\) = 99
Số cần tìm là 4500 hoặc 4499
Ví dụ 5: Tìm số có 3 chữ số biết rằng nếu ta xóa chữ số hàng trăm thì số đó giảm đi 7 lần.
Các dạng bài tập Toán lớp 4, 5 giúp các em học sinh củng cố kỹ năng giải Toán, các dạng bài tập cơ bản và nâng cao: Toán nâng cao lớp 5.
Tham khảo các tài liệu liệu Toán lớp 4 nâng cao
