Các thước đo sự bất bình đẳng thu nhập
Chúng tôi xin giới thiệu bài Các thước đo sự bất bình đẳng thu nhập được VnDoc sưu tầm và tổng hợp nhằm giúp các bạn nắm bắt kiến thức lý thuyết môn Kinh tế công cộng để hoàn thành học phần của mình một cách hiệu quả.
Lưu ý: Nếu bạn muốn Tải bài viết này về máy tính hoặc điện thoại, vui lòng kéo xuống cuối bài viết.
Bài: Các thước đo sự bất bình đẳng thu nhập
Đường Lorenz
Đường Lorenz, được đặt theo tên nhà kinh tế học người Mỹ M.Lorenz (1876-1959), là công cụ tiêu biểu nhằm thể hiện sự bất bình đẳng trong phân phối thu nhập. Đường Lorenz cho biết tỉ lệ phần trăm cộng dồn của thu nhập do một tỉ lệ phần trăm nhất định của dân số sở hữu và thường được biểu thị trong đồ thị hình vuông với trục tung là tỉ lệ phần trăm thu nhập cộng dồn và trục hoành là tỉ lệ phần trăm dân số cộng dồn của các nhóm dân cư theo mức thu nhập tăng dần.
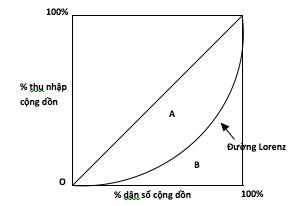
Hình 8.1 Đường Lorenz
Các bước xây dựng đường Lorenz:
- Sắp xếp thu nhập của các cá nhân theo thứ tự tăng dần và chia thành các nhóm có số dân bằng nhau, được gọi là các phân vị. Cách chia thông thường nhất là chia dân số thành 5 nhóm mỗi nhóm 20% và được gọi là ngũ phân vị. Khi đó, tổng cư dân được chia thành ngũ phân vị nghèo nhất, nghèo thứ nhì, trung lưu, giàu thứ nhì và giàu nhất. Việc chia dân số thành càng nhiều phân vị càng đòi hỏi thông tin chi tiết nhưng cũng mang lại sự chính xác hơn trong đo lường bất bình đẳng.
Xác định thu nhập cộng dồn tương ứng với dân số cộng dồn. Ví dụ, đối với ngũ phân vị, các điểm trên đồ thị sẽ thể hiện tỉ lệ phần trăm thu nhập của 20%, 40%, 60%, 80% và 100% dân số theo thu nhập tăng dần. Nối các điểm này lại với nhau ta được đồ thị về đường Lorenz như trong hình 8.1.
Đường Lorenz cho phép hình dung trực quan về mức độ bất bình đẳng trong thu nhập thông qua quan sát hình dạng đường cong. Đường Lorenz càng " võng xuống " - hay nói cách khác càng xa đường chéo của hình vuông - thì mức độ bất bình đẳng càng cao. Tuy nhiên, phương pháp này chỉ dừng lại ở mức định tính. Thêm vào đó, việc kết luận chính xác khi so sánh các đường Lorenz giao nhau là khá khó khăn. Do đó, phương pháp hệ số Gini được đề xuất nhằm khắc phục các điểm yếu này.
Hệ số Gini
Hệ số Gini - đặt tên theo nhà khoa học người Ý C.Gini (1884-1965) - là hình thức lượng hoá đường Lorenz. Hệ số này được tính toàn bằng cách lấy diện tích hình A trong hình 8.1 chia cho diện tích nửa hình vuông bao gồm cả hình A và hình B.
Như vậy, khoảng cách giữa đường Lorenz và đường chéo hình vuông càng lớn thì hệ số Gini (G) càng cao, đồng nghĩa với mức độ bất bình đẳng càng lớn và ngược lại. Hệ số Gini được coi là chỉ số hiệu quả nhất nhằm biểu thị mức độ bất bình đẳng . Tuy nhiên, hạn chế của phương pháp này là trong một số trường hợp hình dạng đường Lorenz là khác nhau (chứng tỏ mức độ bất bình đẳng khác nhau) nhưng cùng diện tích, tuy nhiên hệ số Gini lại giống nhau. Điều này có thể làm sai lệch phép so sánh.
---------------------------------------
Chúng tôi đã giới thiệu nội dung bài Các thước đo sự bất bình đẳng thu nhập về tổng cư dân được chia thành ngũ phân vị nghèo nhất, nghèo thứ nhì, trung lưu, giàu thứ nhì và giàu nhất....
Trên đây, VnDoc đã giới thiệu tới các bạn lý thuyết bài Các thước đo sự bất bình đẳng thu nhập. Các bạn có thể tham khảo thêm một số tài liệu thuộc các chuyên ngành khác trong Cao đẳng - Đại học cũng như Cao học để phục vụ quá trình nghiên cứu hiệu quả hơn.




