Đề thi chọn học sinh giỏi tỉnh môn Toán lớp 10 năm 2017 - 2018 Sở GD&ĐT Hải Dương
VnDoc xin giới thiệu tới thầy cô cùng các bạn học sinh tài liệu Đề thi chọn học sinh giỏi tỉnh môn Toán lớp 10 năm 2017 - 2018 Sở GD&ĐT Hải Dương, tài liệu gồm 5 bài toán tự luận, thời gian làm bài 180 phút, đề thi HSG Toán 10 có lời giải chi tiết.
Đề thi chọn học sinh giỏi tỉnh môn Toán lớp 10
Chi tiết Đề thi chọn học sinh giỏi tỉnh môn Toán lớp 10
Câu I (2,0 điểm)
1) Tìm tất cả các giá trị của tham số m để hàm số y = 6x2 - 4x + 2018/ ![]() \(\sqrt{\left(m-1\right)x^2+2\left(m-1\right)x+4}\) có tập xác định là R.
\(\sqrt{\left(m-1\right)x^2+2\left(m-1\right)x+4}\) có tập xác định là R.
2) Cho hai hàm số y = x2 - 2 (m -1) x - 2m và y = 2x + 3. Tìm m để đồ thị các hàm số đó cắt nhau tại hai điểm A và B phân biệt sao cho OA2 + OB2 nhỏ nhất (trong đó O là gốc tọa độ).
Câu II (3,0 điểm)
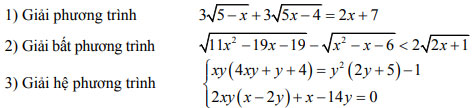
Câu III (3,0 điểm)
1) Cho tam giác ABC có AB = 6; BC = 7; CA = 5. Gọi M là điểm thuộc cạnh AB sao cho AM = 2MB và N là điểm thuộc AC sao cho AN→ = kAC→ (k ∈ R).Tìm k sao cho đường thẳng CM vuông góc với đường thẳng BN.
2) Cho tam giác ABC có BC = a, CA = b, AB = c và p là nửa chu vi của tam giác. Gọi I là tâm đường tròn nội tiếp tam giác. Biết c(p - a)/IA2 + a(p - b)/IB2 + b(p - c)/IC2 = 9/2. Chứng minh rằng tam giác ABC đều.
2) Trong mặt phẳng toạ độ Oxy, cho hình chữ nhật ABCD có phương trình đường thẳng AB là x - 2y +1 = 0. Biết phương trình đường thẳng BD là M (2,1). Biết phương trình đường thẳng BD là x - 7 y +14 = 0 và đường thẳng AC đi qua điểm M(2,1). Tìm toạ độ các đỉnh của hình chữ nhật.
Câu IV (1,0 điểm)
Một xưởng sản xuất có hai máy, sản xuất ra hai loại sản phẩm I và II. Một tấn sản phẩm loại I lãi 2 triệu đồng, một tấn sản phẩm loại II lãi 1,6 triệu đồng. Để sản xuất 1 tấn sản phẩm loại I cần máy thứ nhất làm việc trong 3 giờ và máy thứ hai làm việc trong 1 giờ. Để sản xuất 1 tấn sản phẩm loại II cần máy thứ nhất làm việc trong 1 giờ và máy thứ hai làm việc trong 1 giờ. Mỗi máy không đồng thời làm hai loại sản phẩm cùng lúc. Một ngày máy thứ nhất làm việc không quá 6 giờ, máy thứ hai làm việc không quá 4 giờ. Hỏi một ngày nên sản xuất bao nhiêu tấn mỗi loại sản phẩm để tiền lãi lớn nhất?
Câu V (1,0 điểm)
Chứng minh rằng với mọi số thực a,b, c dương thỏa mãn a2 + b2 + c2 = 27 thì:
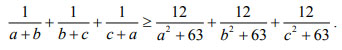
Đề thi học sinh giỏi môn Toán lớp 10 Sở GD&ĐT Hải Dương năm học 2016 - 2017
Đề thi học sinh giỏi môn Toán lớp 10 trường THPT Lý Thái Tổ, Bắc Ninh năm học 2015 - 2016
---------------------------------------------
Trên đây VnDoc.com đã giới thiệu tới bạn đọc tài liệu: Đề thi chọn học sinh giỏi tỉnh môn Toán lớp 10 năm 2017 - 2018 Sở GD&ĐT Hải Dương. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Thi thpt Quốc gia môn Toán, Thi thpt Quốc gia môn Hóa học, Thi thpt Quốc gia môn Vật Lý, Thi thpt Quốc gia môn Sinh học mà VnDoc tổng hợp và đăng tải.




