Đề thi học kì 2 lớp 9 môn Toán Sở GD&ĐT Vĩnh Long năm học 2019 - 2020
Đề thi học kì 2 lớp 9 môn Toán Sở GD&ĐT Vĩnh Long năm 2020
Đề thi học kì 2 lớp 9 môn Toán Sở GD&ĐT Vĩnh Long năm học 2019 - 2020 được VnDoc sưu tầm và đăng tải xin gửi tới bạn đọc cùng tham khảo. Bài viết có kèm lời giải chi tiết cho các bạn đánh giá so sánh, hy vọng tài liệu này sẽ giúp ích cho các bạn học tốt môn Toán lớp 9 này. Mời các bạn cùng tham khảo chi tiết và tải về bài viết dưới đây nhé.
Xem thêm: Đề thi học kì 2 Toán 9 Sở GD&ĐT Vĩnh Long năm 2020 - 2021.
Đề thi Toán học kì 2 lớp 9
I. TỰ LUẬN (8.0 điểm)
Bài 1 (2.0 điểm).
Giải các phương trình và hệ phương trình sau:
\(a)\ x^2 -7x + 12 = 0.\)
\(b)\ x^4-4x^2=0\)
\(c)\ \left\{ \matrix{ 2x+y=5 \hfill \cr 3x-2y = 4 \hfill \cr} \right.\)
\(d)\ x^2-2\sqrt{3}x+2=0\)
Bài 2 (1.0 điểm).
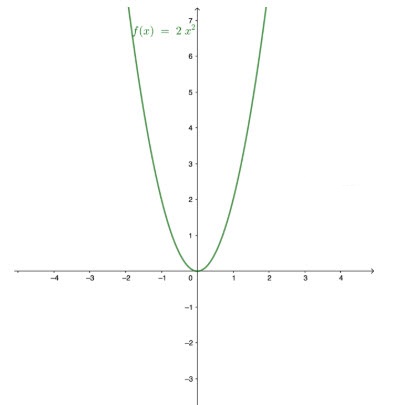
Cho \(Parabol (P): y = 2x^2\) và đường thẳng \((d): y = 2x - m\)
a) Vẽ Parabol (P) trên mặt phẳng tọa độ.
b) Tìm m để Parabol (P) tiếp xúc đường thẳng (d).
Bài 3 (1.0 điểm).
Cho x và y, là hai nghiệm của phương trình \(x^2- 2x-1=0\), không sử dụng máy tính cầm tay, hãy tính giá trị của biểu thức \(P =(x_1)^3 +(x_2)^3.\)
Bài 4 (1.0 điểm).
Một đội xe dự định dùng một số xe cùng loại để chở 120 tấn hàng gửi tặng đồng bào nghèo tỉnh Vĩnh Long. Lúc sắp khởi hành đội được bổ sung thêm 5 xe nữa củng loại. Nhờ vậy, so với ban đầu, mỗi xe chở ít hơn 2 tấn. Hỏi lúc đầu đội có bao nhiêu xe? Biết khối lượng hàng mỗi xe chở như nhau.
Bài 5 (2.5 điểm).
Cho đường tròn (O) và điểm A nằm ngoài đường tròn. Các tiếp tuyến với đường tròn (O) kẻ từ điểm A tiếp xúc với (O) tại B và C. Trên đường tròn (O) lấy điểm M (khác B và C) sao cho M và A nằm về hai phía của đường thẳng BC. Từ M kẻ MH vuông góc với BC, MK vuông góc với AC và MI vuông góc với AB.
a) Chứng minh tứ giác MIBH nội tiếp.
b) Đường thẳng AM cắt đường tròn tại điểm thứ hai N. Chứng minh tam giác ABN đồng dạng với tam giác AMB , từ đó suy ra AB² = AM.AN,
c) Chứng minh MI.MK = MH².
Bài 6 (0.5 điểm). Cho x, y là các số thực dương thỏa mãn x+y=2 Tìm giá trị lớn nhất của \(A = xy(x^3+y^3).\)
II, TRẮC NGHIỆM (2.0 điểm)
Câu 1: Bản kính của hình tròn có chu vi 6π (cm) là
A. 16 cm.
B. 3cm.
C. 9cm
D. 4cm
Câu 2: Phương trình \(x^4 + 3x^2 - 4 = 0\) có bao nhiêu nghiệm?
A. 2.
B. 4.
C. 1
D.3.
Câu 3. Phương trình \(x^2 + 6x-16 = 0\) có tổng các nghiệm bằng
A. 10.
B. -6
C. -3.
D. 3.
Câu 4: Công thức tính diện tích hình tròn tâm 0, bán kính R bằng
A. 2πR
B. 4Rπ
C. Rπ
D. R²π .
Câu 5: Điểm nào sau đây thuộc đồ thị hàm số y = x²?
A. (1;-1).
B. (4;-2).
C. (2;-4).
D. (2;4).
Câu 6: Trong hình vẽ bên dưới, biết góc \(∠ASC = 40°\), SA là tiếp tuyến tại A của đường tròn tâm O. Góc ∠ACS có số đo bằng
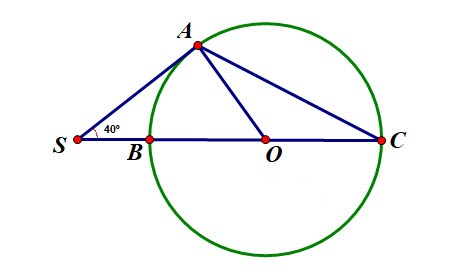
A. 30°
B. 40°
C. 20°
D. 25°
Câu 7: Trên đường tròn tâm O lấy hai điểm A và B sao cho ∠AOB = 60° Số đo cung nhỏ AB bằng
A 25°
B. 310°
C. 60°
D. 100°
Câu 8: Đồ thị hàm số \(y=ax^2\) đi qua điểm M (2;4) thì hệ số a bằng
A. -0,5
B. 2
C. 1
D. 0,5
Hết
Đáp án đề thi học kì 2 lớp 9 môn Toán Sở GD&ĐT Vĩnh Long năm 2020
I. TỰ LUẬN (8.0 điểm)
Bài 1 (2.0 điểm).
\(a)\ x^2 -7x + 12 = 0.\)
\(\Leftrightarrow \left[ \matrix{ x=4 \hfill \cr x=3 \hfill \cr} \right.\)
\(b)\ x^4-4x^2=0\)
\(\Leftrightarrow \left[ \matrix{ x^2=0 \hfill \cr x^2 = 4 \hfill \cr} \right.\)
\(\Leftrightarrow \left[ \matrix{ x=0 \hfill \cr x = 2 \hfill \cr x = -2 \hfill \cr} \right.\)
\(c) \left\{ \matrix{ 2x+y=5 \hfill \cr 3x-2y = 4 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ x=2 \hfill \cr y=1 \hfill \cr} \right.\)
\(d)\ x^2-2\sqrt{3}x+2=0\)
\(\Leftrightarrow \left[ \matrix{ x=1+\sqrt 3 \hfill \cr x=-1+\sqrt 3 \hfill \cr} \right.\)
Bài 2 (1.0 điểm).
a) Vẽ Parabol (P) trên mặt phẳng tọa độ.
b)
Để Parabol (P) tiếp xúc đường thẳng (d) khi và chỉ khi phương trình sau có nghiệm duy nhất:
\(2x^2= 2x - m\)
\(\Leftrightarrow 2x^2- 2x + m =0\)
\(\Leftrightarrow \Delta' = 1^2 -2m =1-2m = 0 \Leftrightarrow m = \dfrac{1}2\)
Bài 3 (1.0 điểm).
Áp dụng hệ thức Vi-ét ta có:
\(\left\{ \matrix{ x_1+x_2 = 2 \hfill \cr x_1x_2 = -1 \hfill \cr} \right.\)
Ta có:
\(P =(x_1)^3 +(x_2)^3 = (x_1+x_2)(x_1^2-x_1x_2 +x_2^2)\)
\(= (x_1+x_2)[(x_1+x_2)^2 - 3x_1x_2] = 2.(2^2+3) = 14\)
Bài 4 (1.0 điểm).
Gọi số xe lúc đầu đội có là A (A ∈ ℕ*)
Theo bài ra ta có:
\(\dfrac{120}{A} - \dfrac{120}{A+5} = 2\)
\(\Leftrightarrow 2A^2 + 10A - 600 = 0\)
\(\Leftrightarrow \left[ \matrix{ A=15 \hfill \cr A=-20 \hfill \cr} \right.\)
vì \(A ∈ ℕ* \Rightarrow A = 15 (xe).\)
Bài 5 (2.5 điểm).
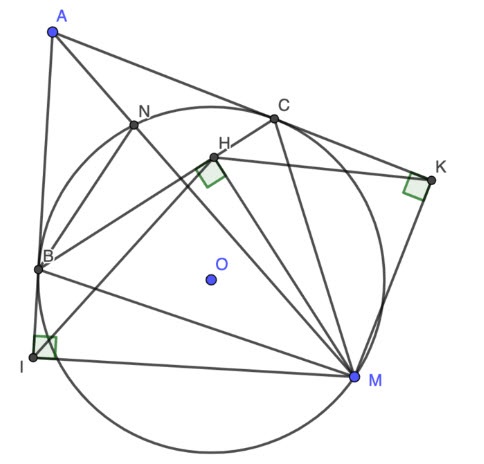
a)
Theo giả thiết có MI ⊥ AB và MH ⊥ BC ⇒ ∠MHB = ∠MIB = 90° ⇒ H I cùng thuộc đường tròn đường kính MB, hay tứ giác MIBH nội tiếp (đpcm).
b)
Theo tính chất góc tạo bởi tia tiếp tuyến và dây cung, ta có: ∠ABN = ∠NMB.
Xét △ABN và △AMB, có:
Góc ∠BAN chung
∠ABN = ∠NMB
Suy ra \(△ABN ∽ △AMB (đpcm1) ⇒ \dfrac{AB}{AN} = \dfrac{AM}{AB} ⇒ AB² = AM.AN (đpcm2).\)
c) Chứng minh MI.MK = MH².
Chứng minh tương tự ý A, ta có tứ giác MIBH, MKCH nội tiếp, đồng thời sử dụng tính chất góc tạo bởi tia tiếp tuyến và dây cung, ta có:
∠MIH = ∠MBH = ∠MCK = ∠MHK.
Tương tự ∠HKM = ∠HCM = ∠MBI = ∠MHI.
Xét △MIH và △MHK, có:
∠MIH = ∠MHK
∠HKM = ∠MHI
Suy ra \(△MIH ∽ △MHK ⇒ \dfrac{MI}{MH} = \dfrac{MH}{MK} ⇒ MI.MK = MH² (đpcm).\)
Bài 6 (0.5 điểm).
Ta có:
\(A = xy(x^3+y^3) = xy(x+y)(x^2-xy+y^2)\)
\(= xy(x+y)[(x+y)^2 - 3xy] = 2xy(4-3xy)\)
\(= -6(xy)^2 + 8xy = -6\left[(xy)^2 - \dfrac{4}3xy + \dfrac{4}9 \right] + \dfrac{8}3\)
\(= -6\left(xy - \dfrac{2}3 \right)^2+ \dfrac{8}3 \leq \dfrac{8}3\) với mọi xy
Hay \({Max}_A = \dfrac{8}3 \Leftrightarrow xy = \dfrac {2}3 \Leftrightarrow (x;y)= \left(\dfrac{3+\sqrt 3}3;\dfrac{3-\sqrt 3}3 \right)\) và hoán vị.
II, TRẮC NGHIỆM (2.0 điểm)
| Câu 1 | B |
| Câu 2 | A |
| Câu 3 | B |
| Câu 4 | D |
| Câu 5 | D |
| Câu 6 | D |
| Câu 7 | C |
| Câu 8 | C |
.......................................................................
Đề thi học kì 2 lớp 9 môn Toán Sở GD&ĐT Vĩnh Long năm học 2019 - 2020 được VnDoc chia sẻ trên đây. Đây là tài liệu hay giúp các bạn học sinh củng cố kiến thức Toán lớp 9, đồng thời là giúp các bạn chuẩn bị tốt kiến thức cho kì thi HK 2 sắp tới. Mời các bạn tham khảo tài liệu trên
Trên đây VnDoc.com vừa gửi tới bạn đọc Đề thi học kì 2 lớp 9 môn Toán Sở GD&ĐT Vĩnh Long năm học 2019 - 2020. Để chuẩn bị cho kì thi học kì 2 lớp 9 sắp tới, các em học sinh cần ôn tập theo đề cương, bên cạnh đó cần thực hành luyện đề để làm quen với nhiều dạng đề khác nhau cũng như nắm được cấu trúc đề thi. Chuyên mục Đề thi học kì 2 lớp 9 và đề thi học kì 2 lớp 9 môn Toán trên VnDoc là tài liệu phong phú và hữu ích cho các em ôn tập và luyện đề. Đây cũng là tài liệu hay cho thầy cô tham khảo ra đề. Mời thầy cô và các em tham khảo.
