Toán 11 Cánh Diều bài 3 trang 104
Từ năm học mới 2023 - 2024, Chương trình Toán lớp 11 sẽ được giảng dạy theo 3 bộ sách: Chân trời sáng tạo; Kết nối tri thức với cuộc sống và Cánh diều. Để giúp các thầy cô và các em học sinh làm quen với từng bộ sách mới, VnDoc xin giới thiệu tài liệu Toán 11 Cánh Diều bài 3 trang 104. Mời quý bạn đọc cùng tham khảo.
Giải Toán 11 Cánh Diều bài 3: Đường thẳng và mặt phẳng song song
- 1. Bài tập 1 trang 104 sgk Toán 11 tập 1 Cánh diều
- 2. Bài tập 2 trang 104 sgk Toán 11 tập 1 Cánh diều
- 3. Bài tập 3 trang 104 sgk Toán 11 tập 1 Cánh diều
- 4. Bài tập 4 trang 104 sgk Toán 11 tập 1 Cánh diều
- 5. Bài tập 5 trang 104 sgk Toán 11 tập 1 Cánh diều
- 6. Bài tập 6 trang 104 sgk Toán 11 tập 1 Cánh diều
1. Bài tập 1 trang 104 sgk Toán 11 tập 1 Cánh diều
Trong phòng học của lớp, hãy nêu những hình ảnh về đường thẳng song song với mặt phẳng.
Bài giải:
Những hình ảnh về đường thẳng song song với mặt phẳng: mép cột dọc với bảng; xà ngang trần nhà với mặt sàn; ...
2. Bài tập 2 trang 104 sgk Toán 11 tập 1 Cánh diều
Trong Hình 57, khi cắt bánh sinh nhật, mặt cắt và mặt khay đựng bánh lần lượt gợi nên hình ảnh mặt phẳng (Q) và mặt phẳng (P); mép trên và mép dưới lát cắt lần lượt gợi nên hình ảnh hai đường thẳng a và b trong đó a song song với mặt phẳng (P). Cho biết hai đường thẳng a, b có song song với nhau hay không.
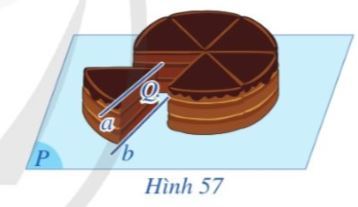
Bài giải:
Hai đường thẳng a, b có song song với nhau vì a song song với (P) mà (Q) cắt (P) tại giao tuyến b.
3. Bài tập 3 trang 104 sgk Toán 11 tập 1 Cánh diều
Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABD, điểm I nằm trên cạnh BC sao cho BI = 2IC. Chứng minh rằng IG song song với mặt phẳng (ACD).
Bài giải:
\(\triangle\)BCE có: E là trung điểm AD
Suy ra: \(\frac{BG}{BE}=\frac{BI}{BC}=\frac{2}{3}\)
Do đó: IG // CE
mà CE thuộc (ACD)
Suy ra: IG // (ACD).
4. Bài tập 4 trang 104 sgk Toán 11 tập 1 Cánh diều
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của AB và CD. Chứng minh rằng đường thẳng MN song song với giao tuyến d của hai mặt phẳng (SBC) và (SAD).
Bài giải:
Ta có: Sx là giao tuyến (SAD) và (SBC) sao cho Sx // AD // BC (1)
Có : M, N là trung điểm của AB, CD
Suy ra: MN // AD // BC (2)
Từ (1)(2) suy ra: MN // Sx.
5. Bài tập 5 trang 104 sgk Toán 11 tập 1 Cánh diều
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Gọi M, N lần lượt là trọng tâm của hai tam giác ABF và ABC. Chứng minh rằng đường thẳng MN song song với mặt phẳng (ACF).
Bài giải:
Gọi I là trung điểm của AB
\(\triangle\)ABF có: M là trọng tâm nên \(\frac{IM}{IF}=\frac{1}{3}\) (1)
\(\triangle\)ABC có: N là trọng tâm nên \(\frac{IN}{IC}=\frac{1}{3}\) (2)
(1)(2) suy ra \(\triangle\)ICF có: \(\frac{IM}{IF}=\frac{IN}{IC}\)
Suy ra: MN // CF mà CF thuộc (ACF) nên MN // (ACF).
6. Bài tập 6 trang 104 sgk Toán 11 tập 1 Cánh diều
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Lấy điểm M trên cạnh AD sao cho AD = 3AM. Gọi G, N lần lượt là trọng tâm của tam giác SAB, ABC.
a) Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD).
b) Chứng minh rằng MN song song với mặt phẳng (SCD) và NG song song với mặt phẳng (SAC).
Bài giải:
a) S là điểm chung của hai mặt phẳng (SAB) và (SCD) mà AB // CD
Từ S kẻ Sx sao cho Sx // AB // CD nên Sx là giao tuyến của hai mặt phẳng (SAB) và (SCD).
b) Gọi I, K là trung điểm của BC, AC
mà hai đường chéo của hình bình hành cắt nhau tại trung điểm mỗi đường
Suy ra K là trung điểm của BD
\(\triangle\)DAB có: \(\frac{DN}{DB}=\frac{DK+KN}{DB}=\frac{\frac{1}{2}DB+\frac{1}{6}DB}{DB}=\frac{2}{3}=\frac{DM}{DA}\)
Suy ra: MN // AB mà AB // CD
Do đó: MN // CD nên MN // (SCD).
Gọi E là trung điểm của AB
G là trọng tâm \(\triangle\)SAB nên \(\frac{EG}{SE}=\frac{1}{3}\)
N là trọng tâm \(\triangle\)ABC nên \(\frac{EN}{EC}=\frac{1}{3}\)
\(\triangle\)ESC có: \(\frac{EG}{SE}=\frac{EN}{EC}\) suy ra GN // SC
mà SC thuộc (SAC). Do đó: GN // (SAC).
-------------------
Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Toán 11 Cánh Diều bài 3 trang 104. Hi vọng qua bài viết này bạn đọc có thêm tài liệu để học tập tốt hơn môn Toán 11 Cánh Diều.
