Toán 11 Cánh Diều bài 3 trang 77

Hàm số liên tục

Từ năm học mới 2023 - 2024, Chương trình Toán lớp 11 sẽ được giảng dạy theo 3 bộ sách: Chân trời sáng tạo; Kết nối tri thức với cuộc sống và Cánh diều. Để giúp các thầy cô và các em học sinh làm quen với từng bộ sách mới, VnDoc xin giới thiệu tài liệu Toán 11 Cánh Diều bài 1 trang 77. Mời quý bạn đọc cùng tham khảo.

Giải Toán 11 Cánh Diều bài 3: Hàm số liên tục

1. Bài tập 1 trang 77 sgk Toán 11 tập 1 Cánh diều
2. Bài tập 2 trang 77 sgk Toán 11 tập 1 Cánh diều
3. Bài tập 3 trang 77 sgk Toán 11 tập 1 Cánh diều
4. Bài tập 4 trang 77 sgk Toán 11 tập 1 Cánh diều
5. Bài tập 5 trang 77 sgk Toán 11 tập 1 Cánh diều
6. Bài tập 6 trang 77 sgk Toán 11 tập 1 Cánh diều

1. Bài tập 1 trang 77 sgk Toán 11 tập 1 Cánh diều

Dùng định nghĩa xét tính liên tục của hàm số $f(x)=2x^{3}+x+1$ $f(x)=2x^{3}+x+1$ tại điểm $x=2$.

Bài giải:

Tập xác định: $\mathbb{R}$ $\mathbb{R}$

Ta có: $f(2)=2.2^{3}+2+1=19$ $f(2)=2.2^{3}+2+1=19$

$\lim_{x\rightarrow 2} f(x)=19$ $\lim_{x\rightarrow 2} f(x)=19$

Do đó: $\lim_{x\rightarrow 2} f(x)=f(2)$ $\lim_{x\rightarrow 2} f(x)=f(2)$

Vậy hàm số đã cho liên tục tại $x=2$.

2. Bài tập 2 trang 77 sgk Toán 11 tập 1 Cánh diều

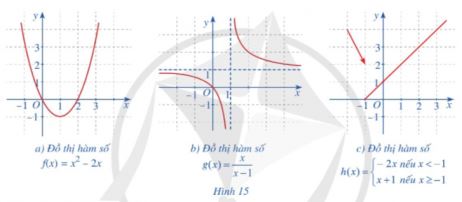
Trong các hàm số có đồ thị ở Hình 15a, 15b, 15c, hàm số nào liên tục trên tập xác định của hàm số đó? Giải thích.

Bài tập 2 trang 77 sgk Toán 11 tập 1 Cánh diều

Bài giải:

a) $f(x)$ là hàm đa thức nên liên tục trên $\mathbb{R}$ $\mathbb{R}$.

b) TXĐ: $\mathbb{R}\setminus \left \{ 1 \right \}$ $\mathbb{R}\setminus \left \{ 1 \right \}$

Do hàm số $g(x)$ là hàm phân thức hữu tỉ nên hàm số liên tục trên mỗi khoảng $(-\infty,1)$ $(-\infty,1)$ và $(1,+\infty)$ $(1,+\infty)$.

c) Ta có: $\lim_{x\rightarrow -1^{-}} h(x)=\lim_{x\rightarrow -1^{-}}(-2x)=2$ $\lim_{x\rightarrow -1^{-}} h(x)=\lim_{x\rightarrow -1^{-}}(-2x)=2$

$\lim_{x\rightarrow -1^{+}} h(x)=\lim_{x\rightarrow -1^{+}}(x+1)=0$ $\lim_{x\rightarrow -1^{+}} h(x)=\lim_{x\rightarrow -1^{+}}(x+1)=0$

$h(-1)=-1+1=0$

Do đó: $\lim_{x\rightarrow -1^{-}} h(x)\neq \lim_{x\rightarrow -1^{+}} h(x)=h(-1)$ $\lim_{x\rightarrow -1^{-}} h(x)\neq \lim_{x\rightarrow -1^{+}} h(x)=h(-1)$

Vậy hàm số $h(x)$ không liên tục tại $x=-1$.

3. Bài tập 3 trang 77 sgk Toán 11 tập 1 Cánh diều

Bạn Nam cho rằng: "Nếu hàm số $y=f(x)$ liên tục tại điểm $x_{0}$ $x_{0}$, còn hàm số $y=g(x)$ không liên tục tại $x_{0}$ $x_{0}$, thì hàm số $y=f(x)+g(x)$ không liên tục tại $x_{0}$ $x_{0}$". Theo em, ý kiến của bạn Nam đúng hay sai? Giải thích.

Bài giải:

Ý kiến đúng.

Giả sử $y=f(x)+g(x)$ liên tục tại $x_{0}$ $x_{0}$.

Đặt $h(x)=f(x)+g(x)$. Ta có: $g(x)=h(x)-f(x)$

Vì $y=h(x), y=f(x)$ liên tục tại $x_{0}$ $x_{0}$ nên hiệu của chúng là hàm số $y=g(x)$ phải liên tục tại $x_{0}$ $x_{0}$.

Điều này trái với đề bài nên do đó ý kiến của Nam là đúng.

4. Bài tập 4 trang 77 sgk Toán 11 tập 1 Cánh diều

Xét tính liên tục của mỗi hàm số sau trên tập xác định của hàm số đó:

a) $f(x)=x^{2}+\sin x$ $f(x)=x^{2}+\sin x$;

b) $g(x)=x^{4}-x^{2}+\frac{6}{x-1}$ $g(x)=x^{4}-x^{2}+\frac{6}{x-1}$;

c) $h(x)=\frac{2x}{x-3}+\frac{x-1}{x+4}$ $h(x)=\frac{2x}{x-3}+\frac{x-1}{x+4}$.

Bài giải:

a) Ta có: $y=x^{2}$ $y=x^{2}$ là hàm đa thức nên liên tục trên $\mathbb{R}$ $\mathbb{R}$.

$y=\sin x$ $y=\sin x$ là hàm lượng giác nên liên tục trên $\mathbb{R}$ $\mathbb{R}$.

Do đó: Hàm số $f(x)=x^{2}+\sin x$ $f(x)=x^{2}+\sin x$ liên tục trên $\mathbb{R}$ $\mathbb{R}$.

b) TXĐ: $\mathbb{R}\setminus \left \{ 1 \right \}$ $\mathbb{R}\setminus \left \{ 1 \right \}$

Ta có: $y=x^{4}-x^{2}$ $y=x^{4}-x^{2}$ là hàm đa thức nên liên tục trên $\mathbb{R}$ $\mathbb{R}$.

Do đó: Hàm số $g(x)=x^{4}-x^{2}+\frac{6}{x-1}$ $g(x)=x^{4}-x^{2}+\frac{6}{x-1}$ liên tục trên mỗi khoảng $(-\infty,1)$ $(-\infty,1)$ và $(1,+\infty)$ $(1,+\infty)$.

c) TXĐ: $\mathbb{R}\setminus \left \{ 3;-4 \right \}$ $\mathbb{R}\setminus \left \{ 3;-4 \right \}$

Hàm số $h(x)=\frac{2x}{x-3}+\frac{x-1}{x+4}$ $h(x)=\frac{2x}{x-3}+\frac{x-1}{x+4}$ liên tục trên mỗi khoảng $(-\infty,-4)$ $(-\infty,-4)$, $(-4,3)$ và $(3,+\infty)$ $(3,+\infty)$.

5. Bài tập 5 trang 77 sgk Toán 11 tập 1 Cánh diều

Cho hàm số

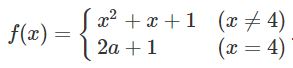Bài tập 5 trang 77 sgk Toán 11 tập 1 Cánh diều .

a) Với $a=0$, xét tính liên tục của hàm số tại $x=4$.

b) Với giá trị nào của $a$ thì hàm số liên tục tại $x=4$?

c) Với giá trị nào của $a$ thì hàm số liên tục trên tập xác định của nó?

Bài giải:

a) Ta có: a=0 thì Bài tập 5 trang 77 sgk Toán 11 tập 1 Cánh diều

Có: $f(4)=1$

$\lim_{x\rightarrow 4} f(x)=4^{2}+4+1=21$ $\lim_{x\rightarrow 4} f(x)=4^{2}+4+1=21$

Do đó: $\lim_{x\rightarrow 4} f(x)\neq f(4)$ $\lim_{x\rightarrow 4} f(x)\neq f(4)$

Vậy hàm số không liên tục tại $x=4$.

b) Ta có: $f(4)=2a+1$

$\lim_{x\rightarrow 4} f(x)=4^{2}+4+1=21$ $\lim_{x\rightarrow 4} f(x)=4^{2}+4+1=21$

Để hàm số liên tục tại $x=4$ thì: $2a+1=21\Leftrightarrow a=10$ $2a+1=21\Leftrightarrow a=10$.

Vậy $a=10$ thì hàm số liên tục tại $x=4$.

c) TXĐ: $\mathbb{R}$ $\mathbb{R}$

Do $f(x)=x^{2}+x+1$ $f(x)=x^{2}+x+1$ nếu $x\neq 4$ $x\neq 4$ nên hàm số liên tục trên mỗi khoảng $(-\infty,4)$ $(-\infty,4)$ và $(4,+\infty)$ $(4,+\infty)$.

Nếu $a=10$ thì hàm số liên tại điểm $x=4$.

Do đó khi $a=10$ thì hàm số liên tục trên $\mathbb{R}$ $\mathbb{R}$.

6. Bài tập 6 trang 77 sgk Toán 11 tập 1 Cánh diều

Hình 16 biểu thị độ cao $h$ (m) của một quả bóng được đá lên theo thời gian $t$ (s), trong đó $h(t)=-2t^{2}+8t$ $h(t)=-2t^{2}+8t$.

a) Chứng tỏ hàm số $h(t)$ liên tục trên tập xác định.

b) Dựa vào đồ thị hãy xác định $\lim_{t\rightarrow 2}(-2t^{2}+8t)$ $\lim_{t\rightarrow 2}(-2t^{2}+8t)$.

Bài tập 6 trang 77 sgk Toán 11 tập 1 Cánh diều

Bài giải:

a) Ta có: $h\geq 0,t\geq 0\Rightarrow -2t^{2}+8t\geq 0\Leftrightarrow 0\leq t\leq 4$ $h\geq 0,t\geq 0\Rightarrow -2t^{2}+8t\geq 0\Leftrightarrow 0\leq t\leq 4$

Suy ra tập xác định hàm số là: $\left [ 0,4 \right ]$ $\left [ 0,4 \right ]$.

Vì hàm số là hàm đa thức nên hàm số liên tục trên đoạn $\left [ 0,4 \right ]$ $\left [ 0,4 \right ]$.

b) $\lim_{t\rightarrow 2} (-2t^{2}+8t)=8$ $\lim_{t\rightarrow 2} (-2t^{2}+8t)=8$

-------------------

Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Toán 11 Cánh Diều bài 3 trang 77. Hi vọng qua bài viết này bạn đọc có thêm tài liệu để học tập tốt hơn môn Toán 11 Cánh Diều.

Chia sẻ, đánh giá bài viết

1

112

Bài trước

Bài sau