Toán 11 Cánh Diều bài 3 trang 56

Cấp số nhân

1 105

Từ năm học mới 2023 - 2024, Chương trình Toán lớp 11 sẽ được giảng dạy theo 3 bộ sách: Chân trời sáng tạo; Kết nối tri thức với cuộc sống và Cánh diều. Để giúp các thầy cô và các em học sinh làm quen với từng bộ sách mới, VnDoc xin giới thiệu tài liệu Toán 11 Cánh Diều trang 56. Mời quý bạn đọc cùng tham khảo.

Giải Toán 11 Cánh Diều bài 3: Cấp số nhân

1. Bài tập 1 trang 56 sgk Toán 11 tập 1 Cánh diều
2. Bài tập 2 trang 56 sgk Toán 11 tập 1 Cánh diều
3. Bài tập 3 trang 56 sgk Toán 11 tập 1 Cánh diều
4. Bài tập 4 trang 56 sgk Toán 11 tập 1 Cánh diều
5. Bài tập 5 trang 56 sgk Toán 11 tập 1 Cánh diều
6. Bài tập 6 trang 56 sgk Toán 11 tập 1 Cánh diều
7. Bài tập 7 trang 56 sgk Toán 11 tập 1 Cánh diều

1. Bài tập 1 trang 56 sgk Toán 11 tập 1 Cánh diều

Trong các dãy số sau, dãy số nào là cấp số nhân? Vì sao?

a) $5; -0,5; 0,05; -0,005; 0,0005$ ;

b) $-9, 3, -1, \frac{1}{3}, -\frac{1}{9}$ ;

c) $2, 8, 32, 64, 256$ .

Bài giải:

a) Vì $\frac{-0,5}{5}=\frac{0,05}{-0,5}=\frac{-0,005}{0,05}=\frac{0,0005}{-0,005}=-\frac{1}{10}$ nên dãy số đã cho là cấp số nhân với $q=-\frac{1}{10}$ .

b) Vì $\frac{3}{-9}=\frac{-1}{3}=\frac{\frac{1}{3}}{-1}=\frac{\frac{-1}{9}}{\frac{1}{3}}=-\frac{1}{3}$ nên dãy số đã cho là cấp số nhân với $q=-\frac{1}{3}$ .

c) Vì $\frac{8}{2}=\frac{32}{8}=\frac{256}{64}\neq \frac{64}{32}$ nên dãy số đã cho không phải là cấp số nhân.

2. Bài tập 2 trang 56 sgk Toán 11 tập 1 Cánh diều

Chứng minh mỗi dãy số ( $u_{n}$ ) với số hạng tổng quát như sau là cấp số nhân:

a) $u_{n}=\frac{-3}{4}.2^{n}$ ;

b) $u_{n}=\frac{5}{3^{n}}$ ;

c) $u_{n}=(-0.75)^{n}$ .

Bài giải:

a) Với $n=1; 2; 3; 4$ ;... ta được dãy số $-\frac{3}{2}; -3;-6;-12$ ;...

Do đó, $u_{n}=\frac{-3}{4}.2^{n}$ là cấp số nhân với $q=2$ .

b) Với $n=1; 2; 3; 4$ ;... ta được dãy số $\frac{5}{3};\frac{5}{9};\frac{5}{27};\frac{5}{81}$ ;...

Do đó, $u_{n}=\frac{5}{3^{n}}$ là cấp số nhân với $q=\frac{1}{3}$ .

c) Với $n=1; 2; 3; 4$ ;... ta được dãy số $-\frac{3}{4};\frac{9}{16};-\frac{27}{64};\frac{81}{256}$ ;...

Do đó, $u_{n}=(-0.75)^{n}$ là cấp số nhân với $q=-\frac{3}{4}$

3. Bài tập 3 trang 56 sgk Toán 11 tập 1 Cánh diều

Cho cấp số nhân ( $u_{n}$ ) với số hạng đầu $u_{n}=-5$ , công bội $q=2$ .

a) Tìm $u_{9}$ .

b) Số $-320$ là số hạng thứ bao nhiêu của cấp số nhân trên?

c) Số $160$ có phải là một số hạng của cấp số nhân trên không?

Bài giải:

a) Ta có số hạng tổng quát: $u_{n}=u_{1}.q^{n-1}=-5.2^{n-1}$ .

Do đó: $u_{9}=(-5).2^{9-1}=-1280$ .

b) Ta có: $-5.2^{n-1}=-320 \Leftrightarrow n=7$ . Vậy -320 là số hạng thứ 7 của cấp số nhân trên.

c) Số 160 không phải là số hạng của cấp số nhân trên.

4. Bài tập 4 trang 56 sgk Toán 11 tập 1 Cánh diều

Cho cấp số nhân ( $u_{n}$ ) với $u_{1}=3, u_{3}=\frac{27}{4}$ .

a) Tìm công bội $q$ và viết năm số hạng đầu của cấp số nhân trên.

b) Tính tổng 10 số hạng đầu của cấp số nhân trên.

Bài giải:

a) $u_{3}= 3.q^{2}=\frac{27}{4}\Leftrightarrow q^{2}=\frac{9}{4}\Leftrightarrow q=\pm \frac{3}{2}$

$q=\frac{3}{2}\Rightarrow$ Năm số hạng đầu: $3;\frac{9}{2};\frac{27}{4};\frac{81}{8};\frac{243}{16}$

$q=-\frac{3}{2}\Rightarrow$ Năm số hạng đầu: $3;-\frac{9}{2};\frac{27}{4};-\frac{81}{8};\frac{243}{16}$

b) $q=\frac{3}{2}\Rightarrow S_{10}=\frac{3.\left [ 1-(\frac{3}{2})^{10} \right ]}{1-\frac{3}{2}}=339,99$

$q=-\frac{3}{2}\Rightarrow S_{10}=\frac{3.\left [ 1-(-\frac{3}{2})^{10} \right ]}{1+\frac{3}{2}}=-67,998$

5. Bài tập 5 trang 56 sgk Toán 11 tập 1 Cánh diều

Một tỉnh có 2 triệu dân vào năm 2020 với tỉ lệ tăng dân số là 1%/năm. Gọi $u_{n}$ là dân số của tỉnh đó sau $n$ năm. Giả sử tỉ lệ tăng dân số là không đổi.

a) Viết công thức tính số dân của tỉnh đó sau $n$ năm kể từ năm 2020.

b) Tính số dân của tỉnh đó sau 10 năm kể từ năm 2020.

Bài giải:

a) $u_{n}=2.0,01^{n-1}$ (triệu dân)

b) $u_{10}=2.0,01^{9}=\frac{2}{100^{9}}$ (triệu dân)

6. Bài tập 6 trang 56 sgk Toán 11 tập 1 Cánh diều

Một gia đình mua một chiếc ô tô giá 800 triệu đồng. Trung bình sau mỗi năm sử dụng, giá trị còn lại của ô tô giảm đi 4% (so với năm trước đó).

a) Viết công thức tính giá trị của ô tô sau 1 năm, 2 năm sử dụng.

b) Viết công thức tính giá trị của ô tô sau $n$ năm sử dụng.

c) Sau 10 năm, giá trị của ô tô ước tính còn bao nhiêu triệu đồng?

Bài giải:

a) Sau 1 năm sử dụng, giá trị ô tô là: $u_{1}=800(1-0,04)$

Sau 2 năm sử dụng, giá trị ô tô là: $u_{2}=800(1-0,04)^{2}$

b) Giá trị ô tô sau n năm sử dụng là: $u_{n}=800(1-0,04)^{n}$

c) Sau 10 năm, giá trị của ô tô ước tính là: $u_{10}=800(1-0,04)^{10}$

7. Bài tập 7 trang 56 sgk Toán 11 tập 1 Cánh diều

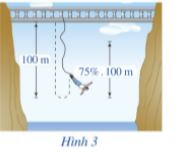
Một người nhảy bungee (một trò chơi mạo hiểm mà người chơi nhảy từ một nơi có địa thế cao xuống với dây đai an toàn buộc xung quanh người) từ một cây cầu và căng một sợi dây dài 100 m. Sau mỗi lần rơi xuống, nhờ sự đàn hồi của dây, người nhảy được kéo lên một quãng đường có độ dài bằng 75% so với lần rơi trước đó và lại bị rơi xuống đúng bằng quãng đường vừa được kéo lên (Hình 3). Tính tổng quãng đường người đó đi được sau 10 lần kéo lên và lại rơi xuống.

Bài tập 7 trang 56 sgk Toán 11 tập 1 Cánh diều

Bài giải:

Tổng quãng đường người đó đi được sau 10 lần kéo lên lại rơi xuống là: $S_{10}=\frac{100(1-0,75^{10})}{1-0,75}$

--------------------

Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Toán 11 Cánh Diều trang 56 bài Cấp số nhân. Hi vọng qua bài viết này bạn đọc có thêm tài liệu để học tập tốt hơn môn Toán 11 Cánh Diều.

Đánh giá bài viết

1 105

Bài trước

Bài sau