Toán 11 Cánh diều bài tập cuối chương 6

Giải Toán 11 Cánh diều

1 169

Giải Toán 11 Cánh diều bài tập cuối chương 6: Hàm số mũ và hàm số logarit

Bài 1 trang 56 SGK Toán 11 Cánh diều
Bài 2 trang 56 SGK Toán 11 Cánh diều
Bài 3 trang 56 SGK Toán 11 Cánh diều
Bài 4 trang 56 SGK Toán 11 Cánh diều
Bài 5 trang 56 SGK Toán 11 Cánh diều
Bài 6 trang 56 SGK Toán 11 Cánh diều
Bài 7 trang 56 SGK Toán 11 Cánh diều
Bài 8 trang 56 SGK Toán 11 Cánh diều
Bài 9 trang 56 SGK Toán 11 Cánh diều
Bài 10 trang 56 SGK Toán 11 Cánh diều
Bài 11 trang 56 SGK Toán 11 Cánh diều
Bài 12 trang 56 SGK Toán 11 Cánh diều
Bài 13 trang 57 SGK Toán 11 Cánh diều
Bài 14 trang 57 SGK Toán 11 Cánh diều
Bài 15 trang 57 SGK Toán 11 Cánh diều
Bài 16 trang 57 SGK Toán 11 Cánh diều
Bài 17 trang 57 SGK Toán 11 Cánh diều
Bài 18 trang 58 SGK Toán 11 Cánh diều
Bài 19 trang 58 SGK Toán 11 Cánh diều
Bài 20 trang 58 SGK Toán 11 Cánh diều
Bài 21 trang 58 SGK Toán 11 Cánh diều
Bài 22 trang 58 SGK Toán 11 Cánh diều
Trắc nghiệm Toán 11 Cánh diều bài tập cuối chương 6

VnDoc.com xin gửi tới bạn đọc bài viết Toán 11 Cánh diều bài tập cuối chương 6 để bạn đọc cùng tham khảo và có thêm tài liệu giải bài tập Toán 11 Cánh diều. Mời các bạn cùng theo dõi bài viết dưới đây nhé.

Bài 1 trang 56 SGK Toán 11 Cánh diều

Điều kiện xác định của x⁻³

A. x ∈ $\mathbb{R}$

B. x ≥ 0

C. x ≠ 0

D. x > 0

Bài làm

Đáp án C là đáp án đúng

Bài 2 trang 56 SGK Toán 11 Cánh diều

Điều kiện xác định của $x^{\frac{3}{5} }$ là:

A. x ∈ $\mathbb{R}$

B. x ≥ 0

C. x ≠ 0

D. x > 0

Bài làm

Đáp án A là đáp án đúng

Bài 3 trang 56 SGK Toán 11 Cánh diều

Tập xác định cảu hàm số y = log_0,5(2x − x2)

A. (−∞;0) ∪ (2;+∞)

B. R $\in$ {0;2}

C. [0;2]

D. (0;2)

Bài làm

Đáp án D

Bài 4 trang 56 SGK Toán 11 Cánh diều

Hàm số nào sau đây đồng biến trên tập xác định của nó?

A. $y=(0,5)^{x}$

B. $y=\left ( \frac{2}{3} \right )^{x}$

C. $y=(\sqrt{2})^{x}$

D. $y=\left ( \frac{e}{\pi} \right )$

Bài làm

Đáp án C

Bài 5 trang 56 SGK Toán 11 Cánh diều

Hàm số nào sau đây nghịch biến trên tập xác định của nó?

A. $log_{3}x$

B. $log_{\sqrt{3}}x$

C. $log_{\frac{1}{e}}x$

D. $y=log_{\pi}x$

Bài làm

Đáp án C

Bài 6 trang 56 SGK Toán 11 Cánh diều

Nếu 3^x = 5 thì 3^2x bằng

A. 15

B. 125

C. 10

D. 25

Bài làm

Đáp án D

Bài 7 trang 56 SGK Toán 11 Cánh diều

Cho A = 4^log₂3. Khi đó giá trị của A bằng:

A. 9

B. 6

C. $\sqrt{3}$

D. 81

Bài làm

Đáp án A

Bài 8 trang 56 SGK Toán 11 Cánh diều

Nếu log_ab = 3 thì log_ab² bằng

A. 9

B. 5

C. 6

D. 8

Bài làm

Đáp án C

Bài 9 trang 56 SGK Toán 11 Cánh diều

Nghiệm của phương trình 3^2x−5 = 27

A. 1

B. 4

C. 6

D. 7

Bài làm

Đáp án B

Bài 10 trang 56 SGK Toán 11 Cánh diều

Nghiệm của phương trình log_0,5(2 − x) = −1

A. 0

B. 2,5

C. 1,5

D. 2

Bài làm

Đáp án A

Bài 11 trang 56 SGK Toán 11 Cánh diều

Tập nghiệm của bất phương trình (0,2)^x> 1

A. (−∞;0,2)

B. (0,2;+∞)

C. (0;+∞)

D. (−∞;0)

Bài làm

Đáp án D

Bài 12 trang 56 SGK Toán 11 Cánh diều

Tập nghiệm của bất phương trình: $log_{\frac{1}{4} } x$ > −2

A. (−∞;16)

B. (16;+∞)

C. (0;16)

D. (−∞;0)

Bài làm

Đáp án C

Bài 13 trang 57 SGK Toán 11 Cánh diều

Cho ba số thực dương a, b, c khác 1 và đồ thị của ba hàm số mũ y = a^x; y = b^x; y = c^x được cho bởi hình 14. Kết luận nào sau đây đúng với ba số a, b, c

A. c < a < b

B. c < b < a

C. a < b < c

D. b < c < a

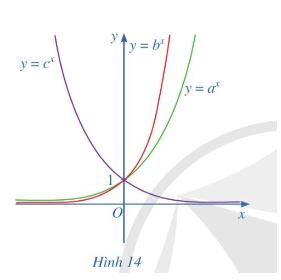
Toán 11 Cánh diều bài tập cuối chương 6

Bài làm

Đáp án A

Bài 14 trang 57 SGK Toán 11 Cánh diều

Cho ba số thực dương a, b, c khác 1 và đồ thị của ba hàm số lôgarit y = log_ax, y = log_bx, y = log_cx được cho bởi hình 15. Kết luận nào sau đây đúng với ba số a, b, c

A. c < a < b

B. c < b < a

C. a < b < c

D. b < c < a

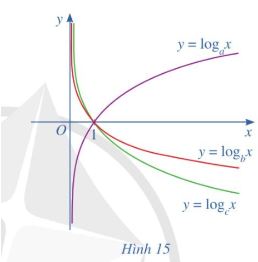
Toán 11 Cánh diều bài tập cuối chương 6

Bài làm

Đáp án D

Bài 15 trang 57 SGK Toán 11 Cánh diều

Viết các biểu thức sau về lũy thừa cơ số a

a) $A=\sqrt[3]{5\sqrt{\frac{1}{5}}}$ với a = 5

b) $B=\frac{4\sqrt[5]{2}}{\sqrt[3]{4}}$ với $a=\sqrt{2}$

Bài làm

a) $A=\sqrt[3]{5\sqrt{\frac{1}{5}}}$

$A=\sqrt[3]{5\left ( \frac{1}{5} \right )^{\frac{1}{2}}}$

$A=\sqrt[3]{5.5^{\frac{-1}{2}}}$

$A=\sqrt[3]{5^{\frac{1}{2}}}=5^{\frac{1}{6}}=a^{\frac{1}{6}}$

b) Có $a=\sqrt{2} => a^{2}=2$

$B=\frac{4\sqrt[5]{2}}{\sqrt[3]{4}}$

$B=\frac{2^{2}.2^{\frac{1}{5}}}{2^{2.\frac{1}{3}}}$

$B=\frac{2^{\frac{11}{5}}}{2^{\frac{2}{3}}}$

$B=\frac{a^{2.\frac{11}{5}}}{a^{2.\frac{2}{3}}}=\frac{a^{\frac{22}{5}}}{a^{\frac{4}{3}}}=a^{\frac{46}{15}}$

Bài 16 trang 57 SGK Toán 11 Cánh diều

Cho x, y là các số thực dương. Rút gọn mỗi biết thức sau

a) $A=\frac{x^{\frac{5}{4}}.y+x.y^{\frac{5}{4}}}{\sqrt[4]{x}.\sqrt[4]{y}}$

b) $B=\left ( \sqrt[7]{\frac{x}{y}\sqrt[5]{\frac{y}{x}}} \right )^{\frac{35}{4}}$

Bài làm

a) $A=\frac{x^{\frac{5}{4}}.y+x.y^{\frac{5}{4}}}{\sqrt[4]{x}.\sqrt[4]{y}}$

$A=\frac{x^{\frac{1}{4}}.x.y+x.y.y^{\frac{1}{4}}}{x^{\frac{1}{4}}+y^{\frac{1}{4}}}$

$A=\frac{xy(x^{\frac{1}{4}}+y^{\frac{1}{4}})}{x^{\frac{1}{4}}+y^{\frac{1}{4}}}=xy$

b) $B=\left ( \sqrt[7]{\frac{x}{y}\sqrt[5]{\frac{y}{x}}} \right )^{\frac{35}{4}}$

$B=\left ( \sqrt[7]{\frac{x}{y}\cdot \left ( \frac{x}{y} \right )^{\frac{-1}{5}}} \right )^{\frac{35}{4}}$

$B=\left ( \sqrt[7]{\left ( \frac{x}{y} \right )^{\frac{4}{5}}} \right )^{\frac{35}{4}}$

$B=\left ( \left ( \frac{x}{y} \right )^{\frac{4}{35}} \right )^{\frac{35}{4}}=\frac{x}{y}$

Bài 17 trang 57 SGK Toán 11 Cánh diều

Tìm tập xác định của mỗi hàm số sau

a) $y=\frac{5}{2^{x}-3}$

b) $y=\sqrt{25-5^{x}}$

c) $y=\frac{x}{1-lnx}$

d) $y=\sqrt{1-log_{3}x}$

Bài làm

a) $y=\frac{5}{2^{x}-3}$

ĐKXĐ: $2^{x}-3\neq 0 => 2^{x}\neq 3$

=> $x\neq log_{2}3$

=> TXĐ: $D=\mathbb{R} \ {log_{2}3}$

b) $y=\sqrt{25-5^{x}}$

ĐKXĐ: $25-5^{x}\geq 0$

=> $5^{x}\leq 5^{2}$

=> $x\leq 2$

TXĐ: $D=(-\infty ;2]$

c) $y=\frac{x}{1-lnx}$

ĐKXĐ: $\left\{\begin{matrix}x>0\\ 1-lnx\neq 0\end{matrix}\right.$

=> $\left\{\begin{matrix}x>0\\ x\neq e\end{matrix}\right.$

$D=(0;+\infty ) \ {e}$

d) $y=\sqrt{1-log_{3}x}$

ĐKXĐ: $\left\{\begin{matrix}x>0\\1-log_{3}x\geq 0\end{matrix}\right.$

=> $\left\{\begin{matrix}x>0\\x\leq 3\end{matrix}\right.$

Bài 18 trang 58 SGK Toán 11 Cánh diều

Cho a > 0, $a\neq 1$ và $a^{\frac{3}{5}}=b$

a) Viết $a^{6}, a^{3}b, \frac{a^{9}}{b^{9}}$ theo lũy thừa cơ số b

b) Tính $log_{a}b, log_{a}(a^{2}b^{5}), log_{\sqrt[5]{a}}\left ( \frac{a}{b} \right )$

Bài làm

a) $a^{6}=(a^{\frac{3}{5}})^{10}=b^{10}$

$a^{3}b=(a^{\frac{3}{5}})^{5}.b=b^{5}.b=b^{6}$

$\frac{a^{9}}{b^{9}}=\frac{(a^{\frac{3}{5}})^{15}}{b^{9}}=\frac{b^{15}}{b^{9}}=b^{6}$

b) $log_{a}b=\frac{3}{5}$

$log_{a}a^{2}b^{5}=log_{a}a^{2}+log_{a}b^{5}=2log_{a}a+5log_{a}b$

$=2+5\cdot \frac{3}{5}=5$

$log_{\sqrt[5]{a}}\left ( \frac{a}{b} \right )=log_{\sqrt[5]{a}}a-log_{\sqrt[5]{a}}b=5log_{a}a-5log_{a}b$

$=5-5\cdot \frac{3}{5}=2$

Bài 19 trang 58 SGK Toán 11 Cánh diều

Giải mỗi phương trình sau:

a) 3^x2−4x+5 = 9

b) 0,5^2x−4 = 4

c) log₃(2x − 1) = 3

d) logx + log(x − 3) = 1

Bài làm

a) $3^{x^{2}-4x+5}=9$

<=> $x^{2}-4x+5=2$

<=> $x^{2}-4x+3=0$

<=> x = 3 hoặc x = 1

b) $0,5^{2x-4}=4$

<=> $2x-4=log_{0,5}4$

<=> 2x - 4 = -2

<=> 2x = 2

<=> x = 1

c) $log_{3}(2x-1)=3$

<=> $log_{3}(2x-1)=log_{3}27$

<=> 2x - 1 = 27

<=> x = 14

d) logx + log(x - 3) = 1

ĐKXĐ: x > 3

<=> $log(x^{2}-3x)=log10$

<=> $x^{2}-3x=10$

<=> $x^{2}-3x-10=0$

<=> x = 5 hoặc x = -2 (không thỏa mãn đkxđ)

=> x = 5

Bài 20 trang 58 SGK Toán 11 Cánh diều

Giải mỗi bất phương trình sau:

a) $5^{x}<0,125$

b) $\left ( \frac{1}{3} \right )^{2x+1}\geq 3$

c) log_0,3> 0

d) ln(x + 4) > ln(2x - 3)

Bài làm

a) $5^{x}<0,125$

<=> $x < log_{5}0,125$

b) $\left ( \frac{1}{3} \right )^{2x+1}\geq 3$

<=> $2x+1\leq log_{\frac{1}{3}}3$

<=> $2x+1\leq -1$

<=> $x\leq -1$

c) log_0,3> 0

<=> x < 1

d) ln(x + 4) > ln(2x - 3)

ĐKXĐ: $x> \frac{3}{2}$

<=> x + 4 > 2x - 3

<=> x < 7

Kết hợp vs ĐKXĐ: $\frac{3}{2}< x <7$

Bài 21 trang 58 SGK Toán 11 Cánh diều

Trong một trận động đất, năng lượng giải toả E (đơn vị: Jun, kí hiệu J) tại tâm địa chấn ở M độ Richter được xác định xấp xỉ bởi công thức: log E ≈ 11,4 + 1,5M.

a) Tính xấp xỉ năng lượng giải toả tại tâm địa chấn ở 5 độ Richter.

b) Năng lượng giải toả tại tâm địa chấn ở 8 độ Richter gấp khoảng bao nhiêu lần năng lượng giải toả tại tâm địa chấn ở 5 độ Richter?

Bài làm

a) Tính xấp xỉ năng lượng giải toả tại tâm địa chấn ở 5 độ Richter:

Thay M = 5 vào công thức, ta có:

logE ≈ 11,4 + 1,5.5 ≈ 18,9

=> E ≈ 10^18,9

b) Tính tỷ lệ năng lượng giải toả tại tâm địa chấn ở 8 độ Richter so với tại tâm địa chấn ở 5 độ Richter:

logE ≈ 11,4 + 1,5.8 ≈ 23,4

=> E ≈ 10^23,4

=> Gấp khoảng 31623 lần

Bài 22 trang 58 SGK Toán 11 Cánh diều

Trong cây cối có chất phóng xạ $_{6}^{14}\textrm{C}$ . Khảo sát một mẫu gỗ cổ, các nhà khoa học đo được độ phóng xạ của nó bằng 86% độ phóng xạ của mẫu gỗ tươi cùng loại. Xác định độ tuổi của mẫu gỗ cổ đó. Biết chu kì bán rã của $_{6}^{14}\textrm{C}$ là T = 5 730 năm, độ phóng xạ của chất phóng xạ tại thời điểm t được cho bởi công thức $H=H_{0}e^{-\lambda t}$ với H₀ là độ phóng xạ ban đầu (tại thời điểm t = 0); $\lambda =\frac{ln2}{T}$ là hằng số phóng xạ

Bài làm

Từ đó, ta có thể tính được hằng số phóng xạ:

$\lambda = \frac{\ln 2}{T} = \frac{\ln 2}{5,730} \approx 0.12$

Giờ ta cần tìm thời gian t mà đã trôi qua từ thời điểm mẫu gỗ cổ được sinh ra đến thời điểm hiện tại. Để tìm thời gian này, ta sử dụng tỷ lệ phóng xạ giữa mẫu gỗ cổ và mẫu gỗ tươi cùng loại:

$\frac{H}{H_0} = 0.86 = e^{-\lambda t}$

t = $\frac{\ln 0.86}{-\lambda} \approx$ 3,078 năm

Vậy độ tuổi của mẫu gỗ cổ đó là khoảng 3,078 năm.

Trắc nghiệm Toán 11 Cánh diều bài tập cuối chương 6

Bài trắc nghiệm số: 4945

------------------------------------------

Bài tiếp theo: Toán 11 Cánh diều bài 1: Định nghĩa đạo hàm. Ý nghĩa hình học của đạo hàm

VnDoc.com vừa gửi tới bạn đọc bài viết Toán 11 Cánh diều bài tập cuối chương 6. Mời các bạn cùng tham khảo thêm tại mục Toán 11 Cánh diều, Trắc nghiệm Toán 11 Cánh diều.

Đánh giá bài viết

1 169

Bài trước

Bài sau