Toán 11 Cánh diều bài 4: Hai mặt phẳng vuông góc
Giải toán 11 Cánh diều bài 4: Hai mặt phẳng vuông góc
VnDoc.com xin gửi tới bạn đọc bài viết Toán 11 Cánh diều bài 4: Hai mặt phẳng vuông góc để bạn đọc cùng tham khảo và có thêm tài liệu giải bài tập Toán 11 Cánh diều nhé. Mời các bạn cùng theo dõi bài viết dưới đây.
Bài 1 trang 100 SGK Toán 11 Cánh diều
Quan sát ba mặt phẳng (P), (Q), (R) ở Hình 57, chỉ ra hai cặp mặt phẳng mà mỗi cặp gồm hai mặt phẳng vuông góc với nhau. Hãy sử dụng kí hiệu để viết những kết quả đó.

Bài làm
(P) ⊥ (R)
(Q) ⊥ (R)
Bài 2 trang 100 SGK Toán 11 Cánh diều
Chứng minh: Nếu hai mặt phẳng vuông góc với nhau thì mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia
Bài làm
Giả sử hai mặt phẳng vuông góc với nhau là (P) và (Q), ta cần chứng minh rằng tồn tại một đường thẳng tương ứng với đường thẳng vuông góc với mặt phẳng (Q) và nằm trên mặt phẳng (P).
Gọi O là giao điểm của hai mặt phẳng (P) và (Q).
Ta lấy một điểm A bất kỳ trên mặt phẳng (Q), và kẻ đường thẳng AO.
Do đó, đường thẳng AO nằm trên mặt phẳng (P), và vì (P) vuông góc với (Q) tại O, nên đường thẳng AO vuông góc với mặt phẳng (Q) tại điểm A.
Vậy ta đã chứng minh được rằng tồn tại một đường thẳng nằm trên mặt phẳng (P) và vuông góc với mặt phẳng (Q), như yêu cầu.
Bài 3 trang 100 SGK Toán 11 Cánh diều
Chứng minh các định lí sau:
a) Nếu hai mặt phẳng (phân biệt) cùng vuông góc với mặt phẳng thứ ba thì song song với nhau hoặc cắt nhau theo một giao tuyến vuông góc với mặt phẳng thứ ba đó;
b) Cho hai mặt phẳng song song. Nếu một mặt phẳng vuông góc với một trong hai
mặt phẳng đó thì vuông góc với mặt phẳng còn lại.
Bài làm
a) Giả sử có hai mặt phẳng vuông góc với một mặt phẳng thứ ba. Khi đó, các mặt phẳng này sẽ tạo thành một hình hộp chữ nhật. Giả sử chúng không song song với nhau, tức là cắt nhau theo một đường thẳng không vuông góc với mặt phẳng thứ ba. Khi đó, ta có thể kết nối hai điểm thuộc hai mặt phẳng vuông góc này và kết quả là ta sẽ thu được một đường thẳng không vuông góc với mặt phẳng thứ ba, mâu thuẫn với giả thiết ban đầu. Vì vậy, hai mặt phẳng này phải song song với nhau hoặc cắt nhau theo một giao tuyến vuông góc với mặt phẳng thứ ba đó.
b) Giả sử có hai mặt phẳng song song và một mặt phẳng vuông góc với một trong hai mặt phẳng đó. Khi đó, đường thẳng vuông góc với mặt phẳng đó sẽ song song với mặt phẳng còn lại. Điều này có thể được chứng minh như sau: Ta chọn một điểm bất kỳ trên mặt phẳng đó, và sau đó kết nối điểm đó với một điểm bất kỳ trên mặt phẳng còn lại. Khi đó, ta thu được một đường thẳng nằm trên mặt phẳng đó và cắt mặt phẳng còn lại theo một giao tuyến. Vì hai mặt phẳng song song nên đường thẳng này sẽ song song với mặt phẳng còn lại, và do đó đường thẳng này cũng sẽ vuông góc với mặt phẳng còn lại. Vậy mặt phẳng ban đầu cũng phải vuông góc với mặt phẳng còn lại.
Bài 4 trang 100 SGK Toán 11 Cánh diều
Cho một đường thẳng không vuông góc với mặt phẳng cho trước. Chứng minh rằng tồn tại duy nhất một mặt phẳng chứa đường thẳng đó và vuông góc với mặt phẳng đã cho
Bài làm
Giả sử đường thẳng đó là d và mặt phẳng cho trước là P. Gọi A là một điểm trên đường thẳng d. Theo định nghĩa, ta có thể vẽ một đường thẳng vuông góc với mặt phẳng P và đi qua điểm A, gọi đường thẳng đó là d'. Vì d' và P vuông góc với nhau nên chúng tạo thành một góc vuông tại A.
Để chứng minh tồn tại mặt phẳng vuông góc với P và chứa đường thẳng d, ta chỉ cần chứng minh rằng mặt phẳng chứa d' cũng vuông góc với P. Điều này tương đương với việc chứng minh rằng đường thẳng d nằm trên mặt phẳng chứa d' và vuông góc với mặt phẳng P.
Giả sử tồn tại một mặt phẳng khác Q cũng vuông góc với mặt phẳng P và chứa đường thẳng d. Vì d nằm trên Q, nên d' cũng nằm trên Q, vì nó là đường thẳng vuông góc với mặt phẳng P và qua điểm A trên d. Như vậy, d' và Q cùng chứa đường thẳng d, do đó chúng trùng nhau, suy ra Q cũng chứa d'. Tức là mặt phẳng Q trùng với mặt phẳng chứa d', và vì thế mặt phẳng Q cũng vuông góc với P.
Vậy, ta đã chứng minh được rằng tồn tại duy nhất một mặt phẳng vuông góc với mặt phẳng P và chứa đường thẳng d.
Bài 5 trang 100 SGK Toán 11 Cánh diều
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, mặt phẳng (SAB) vuông góc với mặt đáy, tam giác SAB vuông cân tại S. Gọi M là trung điểm của AB. Chứng minh rằng:
a) SM ⊥ (ABCD)
b) AD ⊥ (SAB)
c) (SAD) ⊥ (SBC)
Bài làm
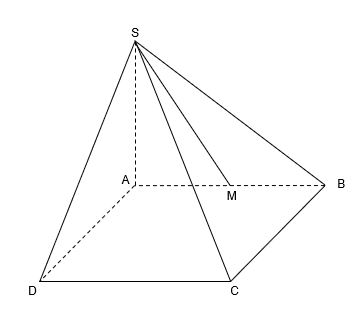
a) Có (SAB) ⊥ (ABCD)
SM ⊥ (ABCD)
b) Có ABCD là hình chữ nhật
=> AD ⊥ AB
Có SM ⊥ (ABCD) => AD ⊥ SM
=> AD ⊥ (SAB)
c) - Có SA ⊥ SB (vì SAB vuông cân tại S)
SA ⊥ BC (vì SA ⊥ (ABCD) )
=> SA ⊥ ( SBC)
=> (SAD) ⊥ (SBC)
----------------------------------------
Bài tiếp theo: Giải toán 11 Cánh diều bài 5: Khoảng cách
VnDoc.com vừa gửi tới bạn đọc bài viết Giải toán 11 Cánh diều bài 4: Hai mặt phẳng vuông góc. Mời các bạn cùng tham khảo thêm tại mục Toán 11 Cánh diều, Trắc nghiệm Toán 11 Cánh diều.









