Toán 11 Cánh Diều bài 4
Từ năm học mới 2023 - 2024, Chương trình Toán lớp 11 sẽ được giảng dạy theo 3 bộ sách: Chân trời sáng tạo; Kết nối tri thức với cuộc sống và Cánh diều. Để giúp các thầy cô và các em học sinh làm quen với từng bộ sách mới, VnDoc xin giới thiệu tài liệu Giải Toán 11 bài 4: Phương trình lượng giác cơ bản CD, Mời quý bạn đọc cùng tham khảo.
Toán 11 Cánh Diều bài 4: Phương trình lượng giác cơ bản
1. Bài tập 1 trang 40 sgk Toán 11 tập 1 Cánh diều
Giải phương trình:
a) 
\(sin(2\pi -\frac{\pi }{3})=-\frac{\sqrt{3}}{2}\);
b) \(sin(3x+\frac{\pi }{4})=-\frac{1}{2}\);
c) \(cos(\frac{x}{2}+\frac{\pi }{4})=\frac{\sqrt{3}}{2}\);
d) \(2cos3x+5=3\);
e) \(3tanx=-\sqrt{3}\);
g) \(cotx-3=\sqrt{3}(1-cotx)\).
Bài giải:
a) \(x=k\pi\) hoặc \(x=\frac{5\pi }{6}+k\pi \left ( k\in \mathbb{Z} \right )\);
b) \(x=-\frac{5\pi }{36}+\frac{k2\pi }{3}\) hoặc \(x=\frac{11\pi }{36}+\frac{k2\pi }{3} \left ( k\in \mathbb{Z} \right )\);
c) \(x=-\frac{\pi }{6}+k4\pi\) hoặc \(x=-\frac{5\pi }{6}+k4\pi \left ( k\in \mathbb{Z} \right )\);
d) \(x=\frac{\pi }{3}+\frac{k2\pi }{3} \left ( k\in \mathbb{Z} \right )\);
e) \(x=-\frac{\pi }{6}+k\pi \left ( k\in \mathbb{Z} \right )\);
g) \(x=\frac{\pi }{6}+k\pi \left ( k\in \mathbb{Z} \right )\).
2. Bài tập 2 trang 40 sgk Toán 11 tập 1 Cánh diều
Giải phương trình:
a) \(sin(2x+\frac{\pi }{4})=sinx\);
b) \(sin2x=cos3x\);
c) \(cos^{2}2x=cos^{2}(x+\frac{\pi }{6})\).
Bài giải:
a) \(x=-\frac{\pi }{4}+k2\pi\) hoặc \(x=\frac{\pi }{4}+\frac{k2\pi }{3} \left ( k\in \mathbb{Z} \right )\)
b) \(cos(\frac{\pi }{2}-2x)=cos3x\Leftrightarrow x=\frac{\pi }{10}-\frac{k2\pi }{5}\) hoặc \(x=-\frac{\pi }{2}+k2\pi \left ( k\in \mathbb{Z} \right )\)
c) \(cos2x=\pm cos(x+\frac{\pi }{6})\Leftrightarrow x=\frac{\pi }{6}+k2\pi\) hoặc \(x=-\frac{\pi }{18}+\frac{k2\pi }{3}\) hoặc \(x=\frac{5\pi }{18}+\frac{k2\pi }{3}\) hoặc \(x=-\frac{5\pi }{6}+k2\pi \left ( k\in \mathbb{Z} \right )\)
3. Bài tập 3 trang 40 sgk Toán 11 tập 1 Cánh diều
Dùng đồ thị hàm số \(y=sinx, y=cosx\) để xác định số nghiệm của phương trình:
a) \(3sinx+2=0\) trên khoảng \((-\frac{5\pi }{2};\frac{5\pi }{2})\);
b) \(cosx=0\) trên đoạn \(\left [ -\frac{5\pi }{2};\frac{5\pi }{2} \right ]\).
Bài giải:
a) Số nghiệm của phương trình \(3sinx+2=0\) trên khoảng \((-\frac{5\pi }{2};\frac{5\pi }{2})\) là 5 nghiệm.
b) Số nghiệm của phương trình \(cosx=0\) trên đoạn \(\left [ -\frac{5\pi }{2};\frac{5\pi }{2} \right ]\) là 6 nghiệm.
4. Bài tập 4 trang 40 sgk Toán 11 tập 1 Cánh diều
Số giờ có ánh sáng mặt trời của một thành phố A ở vĩ độ \(40^{\circ}\) Bắc trong ngày thứ \(t\) của một năm không nhuận được cho bởi hàm số:
\(d(t)=3sin\left [ \frac{\pi }{182}(t-80) \right ]+12\) với \(t\in \mathbb{Z}\) và \(0< t\leq 365\).
a) Thành phố A có đúng 12 giờ có ánh sáng mặt trời vào ngày nào trong năm?
b) Vào ngày nào trong năm thì thành phố A có đúng 9 giờ có ánh sáng mặt trời?
c) Vào ngày nào trong năm thì thành phố A có đúng 15 giờ có ánh sáng mặt trời?
Bài giải:
a) \(sin\left [ \frac{\pi }{182}(t-80) \right ]=0\Leftrightarrow t=80+182k, -\frac{40}{91}< k\leq \frac{285}{182}\)
b) \(sin\left [ \frac{\pi }{182}(t-80) \right ]=-1\Leftrightarrow t=-11+364k, \frac{11}{364}< k\leq \frac{94}{91}\)
c) \(sin\left [ \frac{\pi }{182}(t-80) \right ]=1\Leftrightarrow t=171+364k, -\frac{171}{364}< k\leq \frac{97}{182}\).
5. Bài tập 5 trang 40 sgk Toán 11 tập 1 Cánh diều
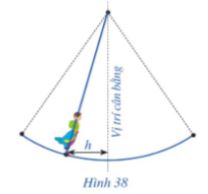
Hội Lim (tỉnh Bắc Ninh) được tổ chức vào mùa xuân thường có trò chơi đánh đu. Khi người chơi đu nhún đều, cây đu sẽ đưa người chơi đu dao động quanh vị trí cân bằng (Hình 38). Nghiên cứu trò chơi này, người ta thấy khoảng cách \(h\) (m) từ vị trí người chơi đu đến vị trí cân bằng được biểu diễn qua thời gian \(t\) (s) (với \(t\geq 0\)) bởi hệ thức \(h=\left | d \right |\) với \(d=3cos\left [ \frac{\pi }{3}(2t-1) \right ]\), trong đó ta quy ước \(d> 0\) khi vị trí cân bằng ở phía sau lưng người chơi đu và \(d< 0\) trong trường hợp ngược lại (Nguồn: Đại số và Giải tích 11 Nâng cao, NXBGD Việt Nam, 2020). Vào thời gian \(t\) nào thì khoảng cách \(h\) là 3 m; 0 m?
Bài giải:
\(h=3\Leftrightarrow \left | 3cos\left [ \frac{\pi }{3}(2t-1) \right ] \right |=3 \Leftrightarrow 3cos\left [ \frac{\pi }{3}(2t-1) \right ]=\pm 3 \Leftrightarrow t=\frac{1}{2}+3k\) hoặc \(t=2+3k \left ( k\in \mathbb{Z} \right )\).
\(h=0 \Leftrightarrow 3cos\left [ \frac{\pi }{3}(2t-1) \right ] =0\Leftrightarrow t=\frac{3\pi }{4}+\frac{1}{2}+\frac{3k}{2} \left ( k\in \mathbb{Z} \right )\).
