Toán 11 Cánh diều bài 5: Khoảng cách
Giải Toán 11 Cánh diều bài 5: Khoảng cách
VnDoc.com xin gửi tới bạn đọc bài viết Giải Toán 11 Cánh diều bài 5: Khoảng cách để bạn đọc cùng tham khảo và có thêm tài liệu giải bài tập Toán 11 Cánh diều nhé. Mời các bạn cùng tham khảo bài viết dưới đây.
Bài 1 trang 106 SGK Toán 11 Cánh diều
Hình 76 gợi nên hình ảnh hai mặt phẳng (P) và (Q) song song với nhau. Cột gỗ cao 4,2 m. Khoảng cách giữa (P) và (Q) là bao nhiêu mét?
Bài làm
Khoảng cách giữa (P) và (Q) là cây cột gỗ gao 4,2m
Bài 2 trang 106 SGK Toán 11 Cánh diều
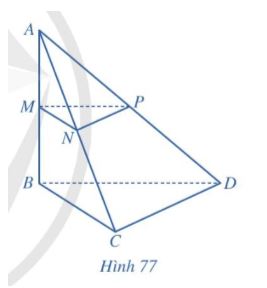
Cho hình tứ diện ABCD có AB = a, BC = b, 
\(\widehat{ABC}\) = \(\widehat{ABD}\) = \(\widehat{BCD}\) = 90∘. Gọi M, N, P lần lượt là trung điểm của AB, AC, AD
a) Tính khoảng cách từ điểm C đến đường thẳng AB.
b) Tính khoảng cách từ điểm D đến mặt phẳng (ABC).
c) Tính khoảng cách giữa hai đường thẳng AB và CD.
Bài làm
a) Có \(\widehat{ABC}\) = 90∘
=> AB ⊥ BC => d(C,AB) = BC = b
b) Có \(AB\perp BC, AB\perp BD\)
=> AB ⊥ (BCD)
=> AB ⊥ CD
mà BC ⊥ CD (Vì \(\widehat{BCD}\) = 90∘)
=> CD ⊥ (ABC)
=> d(D,(ABC)) = CD = \(\sqrt{BD^{2} - BC^{2} } = \sqrt{c^{2}-b^{2} }\)
c) AB ⊥ BC, BC ⊥ CD => d(AB,CD) = BC = b
Bài 3 trang 106 SGK Toán 11 Cánh diều
Với giả thiết ở Bài tập 2, hãy:
a) Chứng minh rằng MN // BC. Tính khoảng cách giữa hai đường thẳng MN và BC.
b) Chứng minh rằng MP // (BCD). Tính khoảng cách từ đường thẳng MP đến mặt phẳng (BCD).
c) Chứng minh rằng (MNP) || (BCD). Tính khoảng cách giữa hai mặt phẳng (MNP) và (BCD).
Bài làm
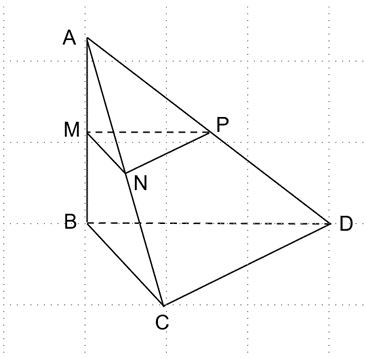
a) Có M là trung điểm của AB, N là trung điểm của AC
=> MN là đường trung bình của tam giác ABC
=> MN // BC
- Có AB ⊥ BC => MB ⊥ BC => d(MN,BC) = MB = \(\frac{1}{2}\)AB = \(\frac{a}{2}\)
b) Có M là trung điểm của AB, P là trung điểm của AD
=> MP là đường trung bình của tam giác ABD
=> MP // BD
mà BD ⊂ (BCD)
=> MP // (BCD)
Có AB ⊥ (BCD) => MB ⊥ (BCD)
=> d(MP,(BCD)) = d(M,(BCD)) = MB = \(\frac{a}{2}\)
c) Có MN // BC, BC ⊂ (BCD)
=> MN // (BCD)
mà MP // (BCD)
=> (MNP) // (BCD)
=> d((MNP), (BCD)) = d(M,(BCD)) = MB = \(\frac{a}{2}\)
Bài 4 trang 106 SGK Toán 11 Cánh diều
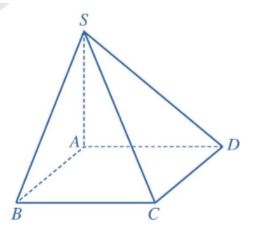
Cho hình chóp S.ABCD có SA ⊥ (ABCD), đáy ABCD là hình vuông cạnh a, SA = a (Hình 78).
a) Tính khoảng cách từ điểm S đến đường thẳng CD.
b) Tính khoảng cách từ điểm D đến mặt phẳng (SAB).
c) Tính khoảng cách từ điểm A đến mặt phẳng (SCD).
Bài làm
a) Có \(SA\perp (ABCD) => SA\perp CD\)
Có ABCD là hình vuông => \(AD \perp CD\)
=> \(CD \perp (SAD) => CD\perp SD\)
=> \(d(S,CD)=SD=\sqrt{SA^{2}+AD^{2}}=a\sqrt{2}\)
b) \(SA\perp (ABCD)=>SA\perp AD\)
ABCD là hình vuông => \(AB\perp AD\)
=> \(AD\perp (SAB)=>d(D,(SAB))=AD=a\)
c) Kẻ \(AH\perp SD\)
\(CD\perp (SAD) => CD\perp AH\)
=> \(AH\perp (SCD)=>d(A,(SCD))=AH\)
Tam giác SAD vuông tại A có đường cao AH
=> \(AH=\frac{SA.AD}{SD}=\frac{a\sqrt{2}}{2}\)
Bài 5 trang 106 SGK Toán 11 Cánh diều
Với giả thiết ở Bài tập 4, hãy:
a) Chứng minh rằng BC // (SAD) và tính khoảng cách giữa BC và mặt phẳng (SAD).
b) Chứng minh rằng BD ⊥ (SAC) và tính khoảng cách giữa hai đường thẳng BD và SC.
Bài làm
a) ABCD là hình vuông => BC // AD
mà \(AD \subset (SAD)\)
=> \(BC // (SAD) => d(BC,(SAD))=d(B, (SAD))\)
\(SA\perp (ABCD) => SA\perp AB\)
ABCD là hình vuông
=> \(AB\perp AD => AB\perp (SAD) => d(B, (SAD))=AB=a\)
b) ABCD là hình vuông => \(BD \perp AC\)
\(SA\perp (ABCD) => SA\perp BD\)
=> \(BD \perp (SAC)\)
Gọi \(O=AC\cap BD\), kẻ \(OH\perp SC\)
Có \(BD \perp (SAC) => BD \perp OH\)
=> d(BD, SC) = OH
Có tam giác ABC vuông tại B
=> \(AC=a\sqrt{2}\)
=> \(OC=\frac{1}{2}AC=\frac{a\sqrt{2}}{2}\)
Có \(SA\perp (ABCD) => SA\perp AC\)
=> Tam giác SAC vuông tại A
=> \(SC=a\sqrt{3}\)
Có \(\Delta SAC\sim \Delta OHC (g.g)\)
=> \(\frac{SA}{OH}=\frac{SC}{OC}\)
=> \(OH=\frac{SA.OC}{SC}=\frac{a\sqrt{6}}{6}\)
--------------------------------------------------
Bài tiếp theo: Giải Toán 11 Cánh diều bài 6: Hình lăng trụ đứng. Hình chóp đều. Thể tích của một số hình khối
VnDoc.com vừa gửi tới bạn đọc bài viết Giải Toán 11 Cánh diều bài 5: Khoảng cách. Mời các bạn cùng tham khảo thêm tại mục Toán 11 Cánh diều, Trắc nghiệm Toán 11 Cánh diều.
