Toán 11 Cánh Diều trang 47, 48

Bài 1: Dãy số

1 359

Từ năm học mới 2023 - 2024, Chương trình Toán lớp 11 sẽ được giảng dạy theo 3 bộ sách: Chân trời sáng tạo; Kết nối tri thức với cuộc sống và Cánh diều. Để giúp các thầy cô và các em học sinh làm quen với từng bộ sách mới, VnDoc xin giới thiệu tài liệu Toán 11 Cánh Diều trang 47, 48. Mời quý bạn đọc cùng tham khảo.

Giải Toán 11 Cánh Diều bài 1: Dãy số

1. Bài tập 1 trang 47 sgk Toán 11 tập 1 Cánh diều
2. Bài tập 2 trang 47 sgk Toán 11 tập 1 Cánh diều
3. Bài tập 3 trang 48 sgk Toán 11 tập 1 Cánh diều
4. Bài tập 4 trang 48 sgk Toán 11 tập 1 Cánh diều
5. Bài tập 5 trang 48 sgk Toán 11 tập 1 Cánh diều
6. Bài tập 6 trang 48 sgk Toán 11 tập 1 Cánh diều

1. Bài tập 1 trang 47 sgk Toán 11 tập 1 Cánh diều

Viết năm số hạng đầu của mỗi dãy số có số hạng tổng quát $u_{n}$ cho bởi công thức sau:

a) $u_{n}=2n^{2}+1$ ;

b) $u_{n}=\frac{(-1)^{n}}{2n-1}$ ;

c) $u_{n}=\frac{2^{n}}{n}$ ;

d) $u_{n}=(1+\frac{1}{n})^{n}$ .

Bài giải:

a) $3, 9, 19, 33, 51$ ;

b) $-1; \frac{1}{3}; -\frac{1}{5}; \frac{1}{7}; -\frac{1}{9}$ ;

c) $2;2;\frac{8}{3}; 4; \frac{32}{5}$ ;

d) $2;\frac{9}{4}; \frac{64}{27}; \frac{625}{256}; (\frac{6}{5})^{5}$ .

2. Bài tập 2 trang 47 sgk Toán 11 tập 1 Cánh diều

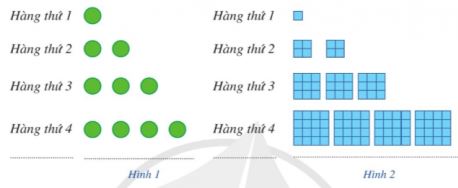
a) Gọi $u_{n}$ là số chấm ở hàng thứ $n$ trong Hình 1. Dự đoán công thức của số hạng tổng quát cho dãy số $(u_{n})$ .

b) Gọi $v_{n}$ là tổng diện tích của các hình tô màu ở hàng thứ $n$ trong Hình 2 (mỗi ô vuông nhỏ là một đơn vị diện tích). Dự đoán công thức của số hạng tổng quát cho dãy số $(v_{n})$ .

Bài tập 2 trang 47 sgk Toán 11 tập 1 Cánh diều

Bài giải:

a) Số hạng tổng quát $u_{n}=n$ .

b) Ta có: $v_{1}=1^{3}$ , $v_{2}=2^{3}$ , $v_{3}=3^{3}$ , $v_{4}=4^{3}$ ...

Do đó: Số hạng tổng quát $v_{n}=n^{3}$ .

3. Bài tập 3 trang 48 sgk Toán 11 tập 1 Cánh diều

Xét tính tăng, giảm của mỗi dãy số ( $u_{n}$ ), biết:

a) $u_{n}=\frac{n-3}{n+2}$ ;

b) $u_{n}=\frac{3^{n}}{2^{n}.n!}$ ;

c) $u_{n}=(-1)^{n}.(2^{n}+1)$ .

Bài giải:

a) Ta có: $u_{n+1}=\frac{n-2}{n+3}$ với mọi $n\in \mathbb{N}^{*}$ .

Có: $u_{n+1}-u_{n}= \frac{5}{n^{2}+5n+6}> 0$ , $n\in \mathbb{N}^{*}$ .

Vậy dãy số $u_{n}$ là dãy số tăng.

b) Ta có: $u_{n+1}-u_{n}< 0$ , với mọi $n\in \mathbb{N}^{*}$ .

Vậy dãy số $u_{n}$ là dãy số giảm.

c) Ta thử số n = 1; 2; 3; ... được dãy số $u_{n}= -3; 5; -9; 17$ ; ...

Vậy dãy số $u_{n}$ là dãy số không tăng không giảm.

4. Bài tập 4 trang 48 sgk Toán 11 tập 1 Cánh diều

Trong các dãy số ( $u_{n}$ ) được xác định như sau, dãy số nào bị chặn dưới, bị chặn trên, bị chặn?

a) $u_{n}= n^{2}+2$ ;

b) $u_{n}=-2n+1$ ;

c) $u_{n}=\frac{1}{n^{2}+n}$ .

Bài giải:

a) Vì $n^{2}+2\geq 3$ nên dãy số $u_{n}$ là dãy số bị chặn dưới;

b) Vì $-2n+1\leq -1$ nên dãy số $u_{n}$ là dãy số bị chặn trên;

c) Vì $0< \frac{1}{n^{2}+n}\leq \frac{1}{2}$ nên dãy số $u_{n}$ là dãy số bị chặn.

5. Bài tập 5 trang 48 sgk Toán 11 tập 1 Cánh diều

Cho dãy số thực dương ( $u_{n}$ ). Chứng minh rằng dãy số ( $u_{n}$ ) là dãy số tăng khi và chỉ khi $\frac{u_{n}+1}{u_{n}}> 1$ với mọi $n\in \mathbb{N}^{*}$ .

Bài giải:

Vì $u_{n}> 0$ nên nhân $u_{n}$ vào hai vế của bất đẳng thức $\frac{u_{n}+1}{u_{n}}> 1$ , ta có: $u_{n+1}> u_{n}$ với mọi $n\in \mathbb{N}^{*}$ .

Suy ra: Dãy số ( $u_{n}$ ) là dãy số tăng khi và chỉ khi $\frac{u_{n}+1}{u_{n}}> 1$ với mọi $n\in \mathbb{N}^{*}$ .

6. Bài tập 6 trang 48 sgk Toán 11 tập 1 Cánh diều

Chị Mai gửi tiền tiết kiệm vào ngân hàng theo thể thức lãi kép như sau: Lần đầu chị gửi 100 triệu đồng. Sau đó, cứ hết 1 tháng chị lại gửi thêm vào ngân hàng 6 triệu đồng. Biết lãi suất của ngân hàng là 0,5% một tháng. Gọi $P_{n}$ (triệu đồng) là số tiền chị có trong ngân hàng sau $n$ tháng.

a) Tính số tiền chị có trong ngân hàng sau 1 tháng.

b) Tính số tiền chị có trong ngân hàng sau 3 tháng.

c) Dự đoán công thức của $P_{n}$ tính theo $n$ .

Bài giải:

a) Sau 1 tháng, chị Mai có: $100(1+0,005)$ (triệu đồng)

b) Sau 3 tháng, chị Mai có: $100(1+0,005)^{3}+6(1+0,005)^{2}$ (triệu đồng)

c) Dự đoán công thức: $P_{n}=100(1+0,005)^{n}+6(1+0,005)^{n-1}$ (triệu đồng).

--------------------

Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Toán 11 Cánh Diều trang 47, 48. Hi vọng qua bài viết này bạn đọc có thêm tài liệu để học tập tốt hơn môn Toán 11 Cánh Diều.

Đánh giá bài viết

1 359

Bài trước

Bài sau