Toán 11 Cánh diều bài 1

Góc lượng giác. Giá trị lượng giác của góc lượng giác CD

1 906

Từ năm học mới 2023 - 2024, Chương trình Toán lớp 11 sẽ được giảng dạy theo 3 bộ sách: Chân trời sáng tạo; Kết nối tri thức với cuộc sống và Cánh diều. Để giúp các thầy cô và các em học sinh làm quen với từng bộ sách mới, VnDoc xin giới thiệu tài liệu Giải Toán 11 bài 1: Góc lượng giác. Giá trị lượng giác của góc lượng giác CD, Mời quý bạn đọc cùng tham khảo.

Giải Toán 11 bài 2: Các phép biến đổi lượng giác CD

Góc lượng giác. Giá trị lượng giác của góc lượng giác

1. Bài tập 1 trang 15 sgk Toán 11 tập 1 CD
2. Bài tập 2 trang 15 sgk Toán 11 tập 1 Cánh diều
3. Bài tập 3 trang 15 sgk Toán 11 tập 1 Cánh diều
4. Bài tập 4 trang 15 sgk Toán 11 tập 1 Cánh diều
5. Bài tập 5 trang 15 sgk Toán 11 tập 1 Cánh diều
6. Bài tập 6 trang 15 sgk Toán 11 tập 1 Cánh diều
7. Trắc nghiệm Toán 11 bài 1

1. Bài tập 1 trang 15 sgk Toán 11 tập 1 CD

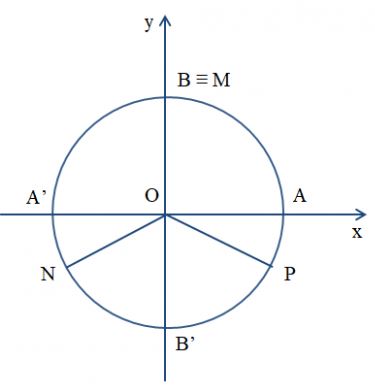
Xác định vị trí các điểm M, N, P trên đường tròn lượng giác sao cho số đo của các góc lượng giác (OA, OM), (OA, ON), (OA, OP) lần lượt bằng $\frac{\pi }{2},\frac{7\pi }{6},\frac{-\pi }{6}$ .

Bài giải:

Điểm M ≡ điểm B thì (OA, OM) = $\frac{\pi }{2}$ .

Điểm N nằm trên cung A'B', sao cho cung A'N = $\frac{1}{3}$ cung A'B' thì (OA, ON) = $\frac{7\pi }{6}$ .

Điểm P nằm trên cung AB', sao cho cung AP = $\frac{1}{3}$ cung AB' thì (OA, OP) = $\frac{-\pi }{6}$ .

Toán 11 Cánh Diều bài 1: Góc lượng giác. Giá trị lượng giác của góc lượng giác

2. Bài tập 2 trang 15 sgk Toán 11 tập 1 Cánh diều

Tính các giá trị lượng giác của mỗi góc sau: 225^∘, −225^∘, −1035^∘, $\frac{5\pi }{3}$ , $\frac{19\pi }{2}$ , $\frac{-159\pi }{4}$ .

Bài giải:

sin(225^∘) = $\frac{-\sqrt{2} }{2}$ , cos(225^∘) = $\frac{-\sqrt{2} }{2}$ , tan(225^∘) = 1, cot(225^∘) = 1

sin(−225^∘) = $\frac{\sqrt{2} }{2}$ , cos(−225^∘) = $\frac{\sqrt{2} }{2}$ , tan(225^∘) = −1, cot(225^∘) = −1

sin (−1035^∘) = $\frac{\sqrt{2} }{2}$ , cos(−1035^∘) = $\frac{\sqrt{2} }{2}$ , tan(−1035^∘) = 1, cot(−1035^∘) = 1

sin( $\frac{5\pi }{3}$ ) = $-\frac{\sqrt{3} }{2}$ , cos( $\frac{5\pi }{3}$ ) = 12, tan( $\frac{5\pi }{3}$ ) = $-\sqrt{3}$ , cot( $\frac{5\pi }{3}$ ) = $-\frac{\sqrt{3} }{3}$

sin( $\frac{19\pi }{2}$ ) = −1, cos( $\frac{19\pi }{2}$ ) = 0, cot( $\frac{19\pi }{2}$ ) = 0

sin( $\frac{-159\pi }{4}$ ) = $-\frac{\sqrt{2} }{2}$ , cos( $\frac{-159\pi }{4}$ ) = $\frac{\sqrt{2} }{2}$ , tan( $\frac{-159\pi }{4}$ ) =−1, cot( $\frac{-159\pi }{4}$ ) = −1

3. Bài tập 3 trang 15 sgk Toán 11 tập 1 Cánh diều

Tính các giá trị lượng giác (nếu có) của mỗi góc sau:

a) $\frac{\pi }{3}$ + k2π (k∈Z);

b) kπ (k∈Z);

c) $\frac{\pi }{2}$ + kπ (k∈Z);

d) $\frac{\pi }{4}$ + kπ (k∈Z).

Bài giải:

a) sin( $\frac{\pi }{3}$ + k2π) = $\frac{\sqrt{3} }{2}$ ; cos ( $\frac{\pi }{3}$ + k2π)= $\frac{1}{2}$ ; tan( $\frac{\pi }{3}$ + k2π) = $-\sqrt{3}$ ; cot( $\frac{\pi }{3}$ + k2π) = $\frac{\sqrt{3} }{3}$ .

b) sin(kπ) = 0; cos(kπ) = −1 nếu k lẻ hoặc =1 nếu k chẵn; tan(kπ) = 0.

c) sin( $\frac{\pi }{2}$ + kπ) = −1 nếu k lẻ hoặc =1 nếu k chẵn; cos( $\frac{\pi }{2}$ +kπ) = 0; cot( $\frac{\pi }{2}$ +kπ) = 0.

d) sin( $\frac{\pi }{4}$ + kπ) = $-\frac{\sqrt{2} }{2}$ nếu k lẻ hoặc = $\frac{\sqrt{2} }{2}$ nếu k chẵn; cos( $\frac{\pi }{4}$ + kπ) = $-\frac{\sqrt{2} }{2}$ nếu k lẻ hoặc = $\frac{\sqrt{2} }{2}$ nếu k chẵn; tan( $\frac{\pi }{4}$ +kπ) = 1; cot( $\frac{\pi }{4}$ +kπ) = 1.

4. Bài tập 4 trang 15 sgk Toán 11 tập 1 Cánh diều

Tính các giá trị lượng giác của góc α trong mỗi trường hợp sau:

a) sinα = $\frac{\sqrt{15} }{4}$ với $\frac{\pi }{2}$ < α < π;

b) cosα = $-\frac{2}{3}$ với −π < α < 0;

c) tanα = 3 với −π < α < 0;

d) cotα = −2 với 0 < α < π.

Bài giải:

a) sinα = $\frac{\sqrt{15} }{4}$ với $\frac{\pi }{2}$ < α < π ⇒ α ≈ 1.318

b) cosα = $-\frac{2}{3}$ với −π < α < 0⇒ α ≈ 2.3

c) tanα = 3 với −π < α < 0⇒ α ≈ 1.249

d) cotα =− 2 với 0 < α < π ⇒ α ≈ −0.464

5. Bài tập 5 trang 15 sgk Toán 11 tập 1 Cánh diều

Tính:

a) A = sin²5^∘+ sin²10^∘+ sin²15^∘+...+ sin²85^∘ (17 số hạng).

b) B = cos5^∘+ cos10^∘+ cos15^∘+...+ cos175^∘ (35 số hạng).

Bài giải:

a) A = cos²85^∘+ cos²80^∘+ cos²75^∘ +...+ sin²45^∘ +...+ sin²85^∘ = $\frac{17}{2}$

b) B = −cos175^∘ − cos170^∘ − cos165^∘ −...+ cos175^∘ = 0

6. Bài tập 6 trang 15 sgk Toán 11 tập 1 Cánh diều

Một vệ tinh được định vị tại vị trí A trong không gian. Từ vị trí A, vệ tinh bắt đầu chuyển động quanh Trái Đất theo quỹ đạo là đường tròn với tâm là tâm O của Trái Đất, bán kính 9000 km. Biết rằng vệ tinh chuyển động hết một vòng của quỹ đạo trong 2h.

a) Hãy tính quãng đường vệ tinh đã chuyển động được sau 1h; 3h; 5h.

b) Vệ tinh chuyển động được quãng đường 200 000 km sau bao nhiêu giờ (làm tròn kết quả đến hàng đơn vị)?

Bài giải:

Ta có công thức độ dài của một cung tròn là: l = R.α

a) Sau 1h, vệ tinh chuyển động được một cung α = π

Như vậy, quãng đường vệ tinh đã chuyển động được sau 1h là: l = 9000π (km).

Sau 3h, vệ tinh chuyển động được một cung α = 3π

Như vậy, quãng đường vệ tinh đã chuyển động được sau 3h là: l = 27000π (km).

Sau 5h, vệ tinh chuyển động được một cung α = 5π

Như vậy, quãng đường vệ tinh đã chuyển động được sau 5h là: l = 45000π (km).

b) Vệ tinh chuyển động được quãng đường 200 000 km sau: $\frac{200000}{9000}$ ≈ 22h.