Đề khảo sát chất lượng đầu năm môn Toán 9 năm 2023 - Đề số 2

Đề thi khảo sát chất lượng đầu năm môn Toán 9 - Đề số 2 do VnDoc biên soạn kèm hướng dẫn chi tiết giúp các bạn học sinh ôn tập, củng cố kiến thức, chuẩn bị kiến thức cho chương trình học môn toán lớp 9 được tốt hơn. Mời các bạn cùng tham khảo chi tiết.

Bản quyền thuộc về VnDoc.
Nghiêm cấm mọi hình thức sao chép nhằm mục đích thương mại.

A. Đề thi khảo sát chất lượng đầu năm môn Toán 9 – Đề số 2

Bài 1 (2 điểm): Giải các phương trình sau:

a, \(4x - 1 = 3x - 2\)	b, \(\left( {3x - 2} \right)\left( {4x + 5} \right) = 0\)
c, \({x^2} - 4x + 3 = 0\)	d, \(\frac{{x - 2}}{{x + 2}} - \frac{3}{{x - 2}} = \frac{{2\left( {x - 11} \right)}}{{{x^2} - 4}}\)

Bài 2 (2 điểm): Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số:

a, \(4x - 3 < 5\)

b, \(\frac{{x + 2}}{4} \ge \frac{1}{2} + \frac{{x - 3}}{3}\)

Bài 3 (2 điểm): Cho biểu thức:

\(A = \left[ {\left( {\frac{1}{{{x^2}}} + 1} \right).\frac{1}{{{x^2} + 2x + 1}} + \frac{2}{{{{\left( {x + 1} \right)}^3}}}.\left( {\frac{1}{x} + 1} \right)} \right]:\frac{{x - 1}}{{{x^3}}}\)

a, Rút gọn biểu thức A

b, Tìm giá trị của x để A = 3

Bài 4 (1 điểm): Giải bài toán bằng cách lập phương trình:

Một người đi từ A đến B với vận tốc 25km/h. Lúc sau người đó đi từ B về A với vận tốc lớn hơn vận tốc ban đầu là 5km/h, vậy nên thời gian đi từ B về A ít hơn 30 phút so với lúc đi. Tính độ dài quãng đường AB.

Bài 5 (2,5 điểm): Cho tam giác nhọn ABC. Vẽ các đường cao AD, BE và CF cắt nhau tại H. Chứng minh:

a, HA.HD = HB.HE = HC.HF

b, Tam giác EHF đồng dạng với tam giác BHC

Bài 6 (0,5 điểm): Chứng minh hằng đẳng thức: \({\left( {x + y} \right)^2} - {\left( {x - y} \right)^2} = 4xy\)

B. Đáp án đề thi khảo sát chất lượng đầu năm môn Toán 9

Bài 1:

a, \(S = \left\{ { - 1} \right\}\)	b, \(S = \left\{ {\frac{{ - 5}}{4};\frac{2}{3}} \right\}\)
c, \(S = \left\{ {1;3} \right\}\)	d, \(S = \left\{ {4;5} \right\}\)

Bài 2:

a, \(x < 2\)

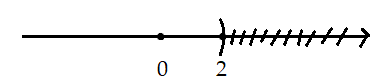
b, \(x \le 12\)

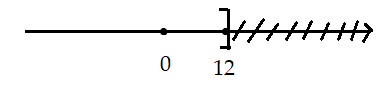
Bài 3:

a, Điều kiện: \(x \ne - 1;x \ne 0;x \ne 1\)

\(A = \left[ {\left( {\frac{1}{{{x^2}}} + 1} \right).\frac{1}{{{x^2} + 2x + 1}} + \frac{2}{{{{\left( {x + 1} \right)}^3}}}.\left( {\frac{1}{x} + 1} \right)} \right]:\frac{{x - 1}}{{{x^3}}}\)

\(= \left[ {\frac{{{x^2} + 1}}{{{x^2}}}.\frac{1}{{{{\left( {x + 1} \right)}^2}}} + \frac{2}{{{{\left( {x + 1} \right)}^3}}}.\frac{{x + 1}}{x}} \right].\frac{{{x^3}}}{{x - 1}}\)

\(= \left[ {\frac{{{x^2} + 1}}{{{x^2}{{\left( {x + 1} \right)}^2}}} + \frac{2}{{x{{\left( {x + 1} \right)}^2}}}} \right].\frac{{{x^3}}}{{x - 1}}\)

\(= \frac{{{x^2} + 1 + 2x}}{{x{{\left( {x + 1} \right)}^2}}}.\frac{{{x^3}}}{{x - 1}}\)

\(= \frac{{{{\left( {x + 1} \right)}^2}}}{{x{{\left( {x + 1} \right)}^2}}}.\frac{{{x^3}}}{{x - 1}} = \frac{{{x^2}}}{{x - 1}}\)

b, Để \(A = 3 \Leftrightarrow \frac{{{x^2}}}{{x - 1}} = 3\)

\(\begin{array}{l} \Leftrightarrow {x^2} = 3\left( {x - 1} \right)\\ \Leftrightarrow {x^2} - 3x + 3 = 0 \end{array}\)

Vì \({x^2} - 3x + 3 = {x^2} - 2.\frac{3}{2}.1 + \frac{9}{4} + \frac{3}{4} = {\left( {x - \frac{3}{2}} \right)^2} + \frac{3}{4} > 0\forall x \ne \pm 1;x \ne 0\)

Nên không tồn tại giá trị của x để

Vậy không tồn tại giá trị của x để A = 3

Bài 4:

Đổi 30 phút = 1/2 giờ

Gọi độ dài quãng đường AB là x (x > 0, km)

Thời gian người đó đi từ A đến B là \(\frac{x}{{25}}\)(giờ)

Vận tốc của người đó lúc đi từ B về A là 25 + 5 = 30 (km/h)

Thời gian người đó đi từ B về A là \(\frac{x}{{30}}\)(giờ)

Thời gian đi từ B về A ít hơn 30 phút so với lúc đi, ta có phương trình:

\(\frac{x}{{25}} - \frac{x}{{30}} = \frac{1}{2}\)

Giải phương trình được x = 75 (thỏa mãn)

Vậy quãng đường AB dài 75km

Bài 5:

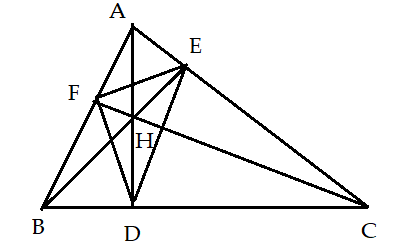
a, + Xét tam giác AEH và tam giác BDH có:

\(\widehat {EHA} = \widehat {DHB}\)(đối đỉnh)

\(\widehat {AEB} = \widehat {HDB} = {90^0}\)(gt)

\(\Rightarrow \Delta AEH\sim\Delta BDH\)(g - g)

\(\Rightarrow \frac{{HA}}{{HB}} = \frac{{HE}}{{HD}} \Rightarrow HA.HD = HB.HE\)(1)

+ Chứng minh tương tự có \(HB.HE = HF.HC\)(2)

+ Từ (1) và (2) suy ra HA.HD = HB.HE = HC.HF

b, + Có HB.HE = HC.HF (cmt) \(\Rightarrow \frac{{HE}}{{HC}} = \frac{{HF}}{{HB}}\)

+ Xét tam giác EHF và tam giác BHC có:

\(\widehat {EHF} = \widehat {CHB}\)(đối đỉnh)

\(\frac{{HE}}{{HC}} = \frac{{HF}}{{HB}}\)(cmt)

Suy ra \(\Delta EHF\sim\Delta BHC\left( {c.g.c} \right)\)

Bài 6:

Xét vế trái:

\(\begin{array}{l} {\left( {x + y} \right)^2} - {\left( {x - y} \right)^2} = {x^2} + 2xy + {y^2} - \left( {{x^2} - 2xy + {y^2}} \right)\\ = {x^2} + 2xy + {y^2} - {x^2} + 2xy - {y^2}\\ = 4xy = VP \end{array}\)

------

Trên đây, VnDoc đã gửi tới các bạn Đề khảo sát chất lượng đầu năm Toán 9 năm 2023 - Đề số 2. Hy vọng đây là tài liệu hữu ích giúp các em làm quen với nhiều dạng đề thi khác nhau, từ đó có sự chuẩn bị tốt cho chương trình học Toán 9 sắp tới. Để xem thêm các đề thi KSCL đầu năm khác, mời các bạn vào chuyên mục Thi KSCL đầu năm lớp 9 trên VnDoc nhé.

Ngoài Đề thi khảo sát chất lượng đầu năm môn Toán 9 trên, các bạn học sinh có thể tham khảo thêm tài liệu học tập lớp 9, bài tập Toán 9, đề thi học kì 1 lớp 9, đề thi học kì 2 lớp 9 đầy đủ, chuẩn bị cho các bài thi đạt kết quả cao. Mời các em cùng tham khảo, luyện tập cập nhật thường xuyên.