VnDoc.com

Giải bài tập Vật lý 10 SBT bài 31

Phương trình trạng thái của khí lí tưởng

Bài trước

Bài sau

Vật lý 10 - Phương trình trạng thái của khí lí tưởng

VnDoc xin giới thiệu tới các bạn học sinh lớp 10 tài liệu Giải bài tập Vật lý 10 SBT bài 31, chắc chắn nội dung tài liệu sẽ giúp các bạn học sinh đạt kết quả cao hơn trong học tập. Mời các bạn học sinh và thầy cô cùng tham khảo.

Giải bài tập Vật lý 10 SBT bài tập cuối chương 4

Giải bài tập Vật lý 10 SBT bài 28

Giải bài tập Vật lý 10 SBT bài 29

Giải bài tập Vật lý 10 SBT bài 30

Giải bài tập Vật lý 10

Bài 31.1 trang 70 Sách bài tập Vật lí 10

Trong quá trình nào sau đây, cả ba thông số trạng thái của một lượng khí xác định đều thay đổi?

A. Không khí bị nung nóng trong một bình đậy kín.

B. Không khí trong một quả bóng bàn bị một học sinh dùng tay bóp bẹp.

C. Không khí trong một xi lanh được nung nóng, dãn nở và đẩy pit tông dịch chuyển.

D. Trong cả ba hiện tượng trên.

Hướng dẫn trả lời:

Chọn đáp án C

Bài 31.2, 31.3, 31.4, 31.5 trang 71 Sách bài tập (SBT) Vật lí 10

31.2. Hệ thức nào sau đây không phù hợp với phương trình trạng thái của khí lí tưởng?

A. pV/T = hằng số.

B. ${{{p_1}{V_1}} \over {{T_1}}} = {{{p_2}{V_2}} \over {{T_2}}}$ ${{{p_1}{V_1}} \over {{T_1}}} = {{{p_2}{V_2}} \over {{T_2}}}$

C. pV ~ T

D. pT/V = hằng số.

Hướng dẫn trả lời:

Chọn đáp án D

31.3. Hệ thức nào sau đây không phù hợp với quá trình đẳng áp?

A. V/T = hằng số.

B. V ~ 1/T

C. V ~ T

D. ${{{V_1}} \over {{T_1}}} = {{{V_2}} \over {{T_2}}}$ ${{{V_1}} \over {{T_1}}} = {{{V_2}} \over {{T_2}}}$

Hướng dẫn trả lời:

Chọn đáp án B

31.4. Đồ thị nào sau đây phù hợp với quá trình đẳng áp?

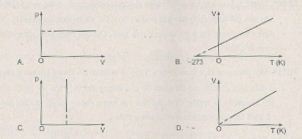
Giải bài tập Vật lý 10 SBT bài 31

Hướng dẫn trả lời:

Chọn đáp án D

31.5. Một lượng khí có thể tích 200 cm³ ở nhiệt độ 16°c và áp suất 740 mmHg. Thể tích của lượng khí này ở điều kiện chuẩn là :

A. V₀= 18,4 cm³.

B. V₀= 1,84 m³.

C. V₀= 184 cm³.

D. V₀= 1,02 m³.

Hướng dẫn trả lời:

Chọn đáp án C

Bài 31.6 trang 72 Sách bài tập (SBT) Vật lí 10

Một lượng khí đựng trong một xilanh có pit-tông chuyển động được, thông số trạng thái của lượng khí này là: 2 atm, 15 lít, 300 K. Khi pit-tông nén khí, áp suất của khí tăng lên tới 3,5 atm, thể tích giảm còn 12 lít. Xác định nhiệt độ của khí nén.

Hướng dẫn trả lời:

${T_2} = {{{p_2}{V_2}{T_1}} \over {{p_1}{V_1}}} = 420K$ ${T_2} = {{{p_2}{V_2}{T_1}} \over {{p_1}{V_1}}} = 420K$

Bài 31.7 trang 72 Sách bài tập (SBT) Vật lí 10

Một bóng thám không được chế tạo để có thể tăng bán kính lên tới 10 m bay ở tầng khí quyển có áp suất 0,03 atm và nhiệt độ 200 K. Hỏi bán kính của bóng khi bơm, biết bóng được bơm khí ở áp suất 1 atm và nhiệt độ 300 K?

Hướng dẫn trả lời:

Áp dụng phương trình trạng thái của khí lí tưởng

${{{p_1}{V_1}} \over {{T_1}}} = {{{p_2}{V_2}} \over {{T_2}}} = > {V_1} = {{{p_2}{V_2}{T_1}} \over {{T_2}{p_1}}}$ ${{{p_1}{V_1}} \over {{T_1}}} = {{{p_2}{V_2}} \over {{T_2}}} = > {V_1} = {{{p_2}{V_2}{T_1}} \over {{T_2}{p_1}}}$

<=> ${4 \over 3}\pi R_1^3 = {{0,03.\left( {{4 \over 3}\pi {{.10}^3}} \right).300} \over {200.1}} = > {R_1} = 3,56m$ ${4 \over 3}\pi R_1^3 = {{0,03.\left( {{4 \over 3}\pi {{.10}^3}} \right).300} \over {200.1}} = > {R_1} = 3,56m$

Bài 31.8 trang 72 Sách bài tập (SBT) Vật lí 10

Tính khối lượng riêng của không khí ở 100°C và áp suất 2.10⁵ Pa. Biết khối lượng riêng của không khí ở 0°C và 1,01.10⁵ Pa là 1,29 kg/m³.

Hướng dẫn trả lời:

Thể tích của 1 kg không khí ở điều kiện tiêu chuẩn là:

${V_0} = {m \over {{\rho _0}}} = {1 \over {1,29}} = 0,78{m^3}$ ${V_0} = {m \over {{\rho _0}}} = {1 \over {1,29}} = 0,78{m^3}$

Ở 0⁰C và 101 kPa: p₀ = 101 kPa

V₀ = 0,78 m³

T₀ = 273 K

Ở 100⁰C và 200 kPa: p = 200 kPa

T = 273 K

V = ?

Ta có ${{{p_0}{V_0}} \over {{T_0}}} = {{pV} \over T} = > V = 0,54{m^3}$ ${{{p_0}{V_0}} \over {{T_0}}} = {{pV} \over T} = > V = 0,54{m^3}$

Do đó $\rho = {{1kg} \over {0,54{m^3}}} = 1,85(kg/{m^3})$ $\rho = {{1kg} \over {0,54{m^3}}} = 1,85(kg/{m^3})$

Bài 31.9 trang 72 Sách bài tập (SBT) Vật lí 10

Một bình cầu dung tích 20 lít chứa ôxi ở nhiệt độ 16°C và áp suất 100 atm. Tính thể tích của lượng khí này ở điều kiện chuẩn. Tại sao kết quả tìm được chỉ là gần đúng?

Hướng dẫn trả lời:

V₀ ≈ 1,889 lít. Vì áp suất quá lớn nên khí không thể coi là khí lí tưởng. Do đó kết quả tìm được chỉ là gần đúng.

Bài 31.10* trang 72 Sách bài tập (SBT) Vật lí 10

Người ta bơm khí ôxi ở điều kiện chuẩn vào một bình có thể tích 5 000 lít. Sau nửa giờ bình chứa đầy khí ở nhiệt độ 24°C và áp suất 765 mmHg. Xác định khối lượng khí bơm vào sau mỗi giây. Coi quá trình bơm diễn ra một cách đều đặn.

Hướng dẫn trả lời:

Sau t giây khối lượng khí trong bình là m = ρΔVt = ρV

Với ρ là khối lượng riêng của khí; ΔV là thể tích khí bơm vào sau mỗi giây và V là thể tích khí bơm vào sau t giây

${{pV} \over T} = {{{p_0}{V_0}} \over {{T_0}}} (1)$ ${{pV} \over T} = {{{p_0}{V_0}} \over {{T_0}}} (1)$

Với $V = {m \over \rho }$ $V = {m \over \rho }$ và $V_0 = {m \over \rho_0 }$ $V_0 = {m \over \rho_0 }$

Thay V và V₀vào (1) ta được: $\rho = {{p{T_0}{\rho _0}} \over {{p_0}T}}$ $\rho = {{p{T_0}{\rho _0}} \over {{p_0}T}}$

Lượng khí bơm vào sau mỗi giây là:

$x = {m \over t} = {{V\rho } \over t} = {V \over t}.{{p{T_0}{\rho _0}} \over {{p_0}T}} = {{5.765.273.1,29} \over {1800.760.297}} = 0,0033kg/s$ $x = {m \over t} = {{V\rho } \over t} = {V \over t}.{{p{T_0}{\rho _0}} \over {{p_0}T}} = {{5.765.273.1,29} \over {1800.760.297}} = 0,0033kg/s$

Bài 31.11* trang 72 Sách bài tập (SBT) Vật lí 10

Một phòng có kích thước 8m x 5m x 4m. Ban đầu không khí trong phòng ở điều kiện chuẩn, sau đó nhiệt độ của không khí tăng lên tới 10°C, trong khi áp suất là 78 cmHg. Tính thể tích của lượng không khí đã ra khỏi phòng và khối lượng không khí còn lại trong phòng.

Hướng dẫn trả lời:

Lượng không khí trong phòng ở trạng thái ban đầu (điều kiện chuẩn):

p₀ = 76 cmHg; V₀ = 5.8.4 = 160 m³; T₀ = 273 K

Lượng không khí trong phòng ở trạng thái 2:

p₂ = 78 cmHg; V₂ ; T₂ = 283 K

Ta có ${{{p_0}{V_0}} \over {{T_0}}} = {{{p_2}{V_2}} \over {{T_2}}} = > {V_2} = {{{p_0}{V_0}{T_2}} \over {{T_0}{p_2}}} = {{76.160.283} \over {273.78}} \approx 161,60({m^3})$ ${{{p_0}{V_0}} \over {{T_0}}} = {{{p_2}{V_2}} \over {{T_2}}} = > {V_2} = {{{p_0}{V_0}{T_2}} \over {{T_0}{p_2}}} = {{76.160.283} \over {273.78}} \approx 161,60({m^3})$

Thể tích không khí thoát ra khỏi phòng

ΔV = V₂ – V₁ = 161,6 – 160 = 1,6 m³.

Thể tích không khí thoát ra khỏi phòng tính ở điều kiện chuẩn là:

${{{p_0}\Delta {V_0}} \over {{T_0}}} = {{{p_2}\Delta V} \over {{T_2}}}$ ${{{p_0}\Delta {V_0}} \over {{T_0}}} = {{{p_2}\Delta V} \over {{T_2}}}$

=> $\Delta {V_0} = {{{p_2}{T_0}\Delta V} \over {{T_2}{p_0}}} = {{78.273.1,6} \over {283.76}} \approx 1,58({m^3})$ $\Delta {V_0} = {{{p_2}{T_0}\Delta V} \over {{T_2}{p_0}}} = {{78.273.1,6} \over {283.76}} \approx 1,58({m^3})$

Khối lượng không khí còn lại trong phòng:

m’ = m – Δm = V₀ρ₀ – ΔV₀ρ₀ = ρ₀(V₀ – ΔV₀)

m’ ≈ 204,84 kg.

Bài 31.12* trang 72 Sách bài tập (SBT) Vật lí 10

Một xilanh có pit-tông cách nhiệt đặt nằm ngang. Pit-tông ở vị trí chia xilanh thành hai phần bằng nhau, chiều dài của mỗi phần là 30 cm. Mỗi phần chứa một lượng khí như nhau ở nhiệt độ 17°C và áp suất 2 atm. Muốn pit-tông dịch chuyển 2 cm thì phải đun nóng khí ở một phần lên thêm bao nhiêu độ? Áp suất của khí khi pit-tông đã dịch chuyển là bao nhiêu?

Hướng dẫn trả lời:

Đối với phần khí bị nung nóng:

+ Trạng thái đầu: p₁; V₁ = lS; T₁ (1)

+ Trạng thái cuối: p₂; V₂ = (l + Δl)S; T₂ (2)

Đối với phần khí không bị nung nóng:

+ Trạng thái đầu: p₁; V₁ = lS; T₁ (1)

+ Trạng thái cuối: p’₂; V’₂ = (l - Δl)S; T’₂ = T₁ (2)

Ta có: ${{{p_1}{V_1}} \over {{T_1}}} = {{{p_2}{V_2}} \over {{T_2}}} = {{{{p$ ${{{p_1}{V_1}} \over {{T_1}}} = {{{p_2}{V_2}} \over {{T_2}}} = {{{{p'}_2}{{V'}_2}} \over {{T_1}}}$

Vì pit-tông ở trạng thái cân bằng nên p’₂ = p₂. Do đó

${{{p_2}{V_2}} \over {{T_2}}} = {{{p_2}{{V$ ${{{p_2}{V_2}} \over {{T_2}}} = {{{p_2}{{V'}_2}} \over {{T_1}}} = > {{{p_2}\left( {l + \Delta l} \right)S} \over {{T_2}}} = {{{p_2}\left( {l - \Delta l} \right)S} \over {{T_1}}}$

=> ${T_2} = {{l + \Delta l} \over {l - \Delta l}}{T_1}$ ${T_2} = {{l + \Delta l} \over {l - \Delta l}}{T_1}$

Vậy phải đun nóng khí ở một bên lên thêm ΔT độ:

$\Delta T = {T_2} - {T_1} = {{l + \Delta l} \over {l - \Delta l}}{T_1} - {T_1} = {{2\Delta l} \over {l - \Delta l}}{T_1} = {{2.0,02} \over {0,3 - 0,02}}.290 = 41,4K$ $\Delta T = {T_2} - {T_1} = {{l + \Delta l} \over {l - \Delta l}}{T_1} - {T_1} = {{2\Delta l} \over {l - \Delta l}}{T_1} = {{2.0,02} \over {0,3 - 0,02}}.290 = 41,4K$

Vì ${{{p_1}{V_1}} \over {{T_1}}} = {{{p_2}{V_2}} \over {{T_2}}}$ ${{{p_1}{V_1}} \over {{T_1}}} = {{{p_2}{V_2}} \over {{T_2}}}$nên:

${p_2} = {{{p_1}{V_1}{T_2}} \over {{T_1}{V_2}}} = {{{p_1}lS\left( {{T_1} + \Delta T} \right)} \over {{T_1}\left( {l + \Delta l} \right)S}}$ ${p_2} = {{{p_1}{V_1}{T_2}} \over {{T_1}{V_2}}} = {{{p_1}lS\left( {{T_1} + \Delta T} \right)} \over {{T_1}\left( {l + \Delta l} \right)S}}$ $= {{{p_1}l\left( {{T_1} + \Delta T} \right)} \over {{T_1}\left( {l + \Delta l} \right)}}$ $= {{{p_1}l\left( {{T_1} + \Delta T} \right)} \over {{T_1}\left( {l + \Delta l} \right)}}$

Thay số vào ta được:

${p_2} = {{2.0,3.\left( {290 + 41} \right)} \over {290\left( {0,3 + 0,02} \right)}} \approx 2,14(atm)$ ${p_2} = {{2.0,3.\left( {290 + 41} \right)} \over {290\left( {0,3 + 0,02} \right)}} \approx 2,14(atm)$

-------------------------

Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Giải bài tập Toán 10, Giải bài tập Vật Lí 10, Giải bài tập Sinh học 10, Giải bài tập Hóa học 10 mà VnDoc tổng hợp và đăng tải.

Chia sẻ, đánh giá bài viết

1

714

Bài trước

Bài sau