Toán 11 Chân trời sáng tạo bài tập cuối chương 6

Hàm số và hàm số Lôgarit

Toán 11 Chân trời sáng tạo bài tập cuối chương 6: Hàm số và hàm số Lôgarit

Bài 1 trang 34 SGK Toán 11 Chân trời
Bài 2 trang 34 SGK Toán 11 Chân trời
Bài 3 trang 34 SGK Toán 11 Chân trời
Bài 4 trang 34 SGK Toán 11 Chân trời
Bài 5 trang 34 SGK Toán 11 Chân trời
Bài 6 trang 34 SGK Toán 11 Chân trời
Bài 7 trang 34 SGK Toán 11 Chân trời
Bài 8 trang 34 SGK Toán 11 Chân trời
Bài 9 trang 34 SGK Toán 11 Chân trời
Bài 10 trang 34 SGK Toán 11 Chân trời
Bài 11 trang 35 SGK Toán 11 Chân trời
Bài 12 trang 35 SGK Toán 11 Chân trời
Bài 13 trang 35 SGK Toán 11 Chân trời
Bài 14 trang 35 SGK Toán 11 Chân trời
Bài 15 trang 35 SGK Toán 11 Chân trời
Bài 16 trang 35 SGK Toán 11 Chân trời
Bài 17 trang 35 SGK Toán 11 Chân trời
Bài 18 trang 35 SGK Toán 11 Chân trời

VnDoc.com xin gửi tới bạn đọc bài viết Toán 11 Chân trời sáng tạo bài tập cuối chương 6: Hàm số và hàm số Lôgarit để bạn đọc cùng tham khảo. Mời các bạn cùng theo dõi để có thêm tài liệu giải bài tập Toán 11 Chân trời sáng tạo nhé.

Bài 1 trang 34 SGK Toán 11 Chân trời

Rút gọn biểu thức $\left [ \left ( \frac{1}{3} \right )^{2} \right ]^{\frac{1}{4}}(\sqrt{3})^{5}$ $\left [ \left ( \frac{1}{3} \right )^{2} \right ]^{\frac{1}{4}}(\sqrt{3})^{5}$, ta được

A. $\sqrt{3}$ $\sqrt{3}$

B. $3.\sqrt{3}$ $3.\sqrt{3}$

C. $\frac{1}{\sqrt{3}}$ $\frac{1}{\sqrt{3}}$

D. 9

Bài làm

Đáp án D

Bài 2 trang 34 SGK Toán 11 Chân trời

Nếu $2^{\alpha}=9 thì (\frac{1}{16})^{\frac{\alpha}{8}}$ $2^{\alpha}=9 thì (\frac{1}{16})^{\frac{\alpha}{8}}$ có giá trị bằng:

A. $\frac{1}{3}$ $\frac{1}{3}$

B. 3

C. $\frac{1}{9}$ $\frac{1}{9}$

D. $\frac{1}{\sqrt{3}}$ $\frac{1}{\sqrt{3}}$

Bài làm

$(\frac{1}{16})^{\frac{\alpha}{8}} = (2^{-4})^{\frac{\alpha}{8}} = 2^{\frac{-\alpha}{2}} = (2^{\alpha})^{\frac{-1}{2}} = 9^{\frac{-1}{2}} = \frac{1}{3}$ $(\frac{1}{16})^{\frac{\alpha}{8}} = (2^{-4})^{\frac{\alpha}{8}} = 2^{\frac{-\alpha}{2}} = (2^{\alpha})^{\frac{-1}{2}} = 9^{\frac{-1}{2}} = \frac{1}{3}$

Đáp án: A

Bài 3 trang 34 SGK Toán 11 Chân trời

Nếu $a^{\frac{1}{2}}=b (a>0;a \neq 1)$ $a^{\frac{1}{2}}=b (a>0;a \neq 1)$ thì:

A. $log_{\frac{1}{2}}a=b$ $log_{\frac{1}{2}}a=b$

B. $2log_{a}b = 1$ $2log_{a}b = 1$

C. $log_{a}\frac{1}{2} = b$ $log_{a}\frac{1}{2} = b$

D. $log_{\frac{1}{2}}b=a$ $log_{\frac{1}{2}}b=a$

Bài làm

Đáp án B

Bài 4 trang 34 SGK Toán 11 Chân trời

Nếu $x=log_{3}4+log_{9}4 thì 3^{x}$ $x=log_{3}4+log_{9}4 thì 3^{x}$ có giá trị bằng:

A. 6

B. 8

C. 16

D. 64

Bài làm

$3^{x}=3^{log_{3}4+log_{9}4}=3^{log_{3}4}.3^{log_{9}4} = 4 + (9^{\frac{1}{2}})^{log_{9}4}=4+(9^{log_{9}4})^{\frac{1}{2}}=4+4^{\frac{1}{2}}=4+2=6$ $3^{x}=3^{log_{3}4+log_{9}4}=3^{log_{3}4}.3^{log_{9}4} = 4 + (9^{\frac{1}{2}})^{log_{9}4}=4+(9^{log_{9}4})^{\frac{1}{2}}=4+4^{\frac{1}{2}}=4+2=6$

Đáp án: A

Bài 5 trang 34 SGK Toán 11 Chân trời

Cho $\alpha,\beta$ $\alpha,\beta$ là hai số thức $\alpha < \beta$ $\alpha < \beta$. Khẳng định nào sau đây đúng?

A. $(0,3)^{\alpha} < (0,3)^{\beta}$ $(0,3)^{\alpha} < (0,3)^{\beta}$

B. $\pi^{\alpha} \geq \pi^{\beta}$ $\pi^{\alpha} \geq \pi^{\beta}$

C. $(\sqrt)^{\alpha} < (\sqrt)^{\beta}$ $(\sqrt)^{\alpha} < (\sqrt)^{\beta}$

D. $(\frac{1}{2})^{\beta} > (\frac{1}{2})^{\alpha}$ $(\frac{1}{2})^{\beta} > (\frac{1}{2})^{\alpha}$

Bài làm

Đáp án C

Bài 6 trang 34 SGK Toán 11 Chân trời

Hình nào vẽ đồ thị của hàm số $y=log_{\frac{1}{2}}x$ $y=log_{\frac{1}{2}}x$?

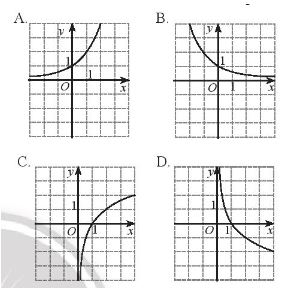
Toán 11 Chân trời sáng tạo bài tập cuối chương 6

Bài làm

Đáp án D

Bài 7 trang 34 SGK Toán 11 Chân trời

Phương trình $0,1^{2x-1}=100$ $0,1^{2x-1}=100$ có nghiệm là:

A. $-\frac{1}{2}$ $-\frac{1}{2}$

B. $\frac{1}{3}$ $\frac{1}{3}$

C. $1\frac{1}{2}$ $1\frac{1}{2}$

D. $2\frac{1}{3}$ $2\frac{1}{3}$

Bài làm

Đáp án A

Bài 8 trang 34 SGK Toán 11 Chân trời

Tập nghiệm của bất phương trình là

A. $(-\infty;1)$ $(-\infty;1)$

B. $(1;+\infty)$ $(1;+\infty)$

C. (0;1)

D. $(-\infty; -\frac{1}{3})$ $(-\infty; -\frac{1}{3})$

Bài làm

Đáp án A

Bài 9 trang 34 SGK Toán 11 Chân trời

Nếu logx= 2log5 - log2 thì

A. x = 8

B. x = 23

C. x = 12,5

D. x = 5

Bài làm

Đáp án C

Bài 10 trang 34 SGK Toán 11 Chân trời

Số nguyên x nhỏ nhất thoả mãn $log_{0,1}(1-2x) > -1$ $log_{0,1}(1-2x) > -1$ là:

A. x = 0

B. x = 1

C. x = -5

D. x = -4

Bài làm

Đáp án D

Bài 11 trang 35 SGK Toán 11 Chân trời

Biết 4^α + 4^−α = 5

Tính giá trị của các biểu thức:

a) 2^α + 2^−α

b) 4^2α + 4^−2α

Bài làm

a) 4^α + 4^−α = 5

⇔(2^α)² + 2.2^α.2^−α + (2^−α)² = 5+2

⇔(2^α + 2^−α)² = 7

⇔2^α + 2^−α = $\sqrt{7}$ $\sqrt{7}$

b) 4^2α + 4^−2α = (4^α)² + 2.4^α.4^−α+ (4^−α)²− 2 = (4^α + 4^−α)²− 2 = 5² − 2 =23

Bài 12 trang 35 SGK Toán 11 Chân trời

Tính giá trị của các biểu thức:

a) $log_{2}72 - \frac{1}{2}(log_{2}3 + log_{2}27)$ $log_{2}72 - \frac{1}{2}(log_{2}3 + log_{2}27)$

b) $5^{log_{2}40-log_{2}5}$ $5^{log_{2}40-log_{2}5}$

c) $3^{2+log_{9}2}$ $3^{2+log_{9}2}$

Bài làm

a) $log_{2}72 - \frac{1}{2}(log_{2}3 + log_{2}27)$ $log_{2}72 - \frac{1}{2}(log_{2}3 + log_{2}27)$

= $log_{2}72-\frac{1}{2}.log_{2}(3.27)$ $log_{2}72-\frac{1}{2}.log_{2}(3.27)$

= $log_{2}72-\frac{1}{2}.log_{2}81$ $log_{2}72-\frac{1}{2}.log_{2}81$

= $log_{2}72-.log_{2}81^{\frac{1}{2}}$ $log_{2}72-.log_{2}81^{\frac{1}{2}}$

= $log_{2}72-.log_{2}9$ $log_{2}72-.log_{2}9$

= $log_{2}\frac{72}{9}$ $log_{2}\frac{72}{9}$

= $log_{2}8=3$ $log_{2}8=3$

b) $5^{log_{2}40-log_{2}5} = 5^{log_{2}\frac{40}{5}}=5^{log_{2}8}=5^{3}=125$ $5^{log_{2}40-log_{2}5} = 5^{log_{2}\frac{40}{5}}=5^{log_{2}8}=5^{3}=125$

c) $3^{2+log_{9}2} = (9^{\frac{1}{2}})^{log_{9}.81+log_{9}2}=9^{\frac{1}{2}.log_{9}(81.2)}=9^{\frac{1}{2}.log_{9}162}=9^{log_{9}162^{\frac{1}{2}}}$ $3^{2+log_{9}2} = (9^{\frac{1}{2}})^{log_{9}.81+log_{9}2}=9^{\frac{1}{2}.log_{9}(81.2)}=9^{\frac{1}{2}.log_{9}162}=9^{log_{9}162^{\frac{1}{2}}}$

= $162^{\frac{1}{2}}=9\sqrt{2}$ $162^{\frac{1}{2}}=9\sqrt{2}$

Bài 13 trang 35 SGK Toán 11 Chân trời

Biết rằng 5^x = 3 và 3^y = 5 . Không sử dụng máy tính cầm tay, tính giá trị của xy

Bài 14 trang 35 SGK Toán 11 Chân trời

Viết công thức biểu thị y theo x, biết $2log_{2}y = 2+\frac{1}{2}log_{2}x$ $2log_{2}y = 2+\frac{1}{2}log_{2}x$

Bài 15 trang 35 SGK Toán 11 Chân trời

Giải các phương trình:

a) $(\frac{1}{4})^{x-2} = \sqrt{8}$ $(\frac{1}{4})^{x-2} = \sqrt{8}$

b) $9^{2x-1} = 81.27^{x}$ $9^{2x-1} = 81.27^{x}$

c) $2log_{5}(x-2)=log_{5}9$ $2log_{5}(x-2)=log_{5}9$

d) $log_{2}(3x+1) = 2 - log_{2}(x-1)$ $log_{2}(3x+1) = 2 - log_{2}(x-1)$

Bài 16 trang 35 SGK Toán 11 Chân trời

Giải các bất phương trình sau:

a) $(\frac{1}{9})^{x+1} > \frac{1}{81}$ $(\frac{1}{9})^{x+1} > \frac{1}{81}$

b) $(\sqrt[4]{3})^{x} \leq 27.3^{x}$ $(\sqrt[4]{3})^{x} \leq 27.3^{x}$

c) $log_{2}(x+1) \leq log_{2}(2-4x)$ $log_{2}(x+1) \leq log_{2}(2-4x)$

Bài 17 trang 35 SGK Toán 11 Chân trời

Thực hiện một mẻ nuôi cấy vi khuẩn với 1000 vi khuẩn ban đầu, nhà sinh học phát hiện ra số lượng vi khuẩn tăng thêm 25% sau mỗi hai ngày,

a) Công thức P(t) = P₀.a^t cho phép tính số lượng vi khuẩn của mẻ nuôi cấy sau t ngày kể từ thời điểm ban đầu. Xác định các tham số P₀ và a (a > 0). Làm tròn a đến hàng phần trăm

b) Sau 5 ngày thì số lượng vi khuẩn bằng bao nhiêu? Làm tròn kết quả đến hàng phầm trăm

c) Sau bao nhiêu ngày thì số lượng vi khuẩn vượt gấp đôi số lượng ban đầu? Làm tròn kết quả đến hàng phần mười.

Bài 18 trang 35 SGK Toán 11 Chân trời

Nhắc lại rằng, độ pH của một dung dịch được tính theo công thức pH = log[H⁺], trong đó [H⁺] là nồng độ H⁺ của dung dịch đó tính bằng mol/L. Nồng độ H⁺ trong dung dịch cho biết độ acid của dung dịch đó.

a) Dung dịch acid A có độ pH bằng 1,9; dung dịch acid B có độ pH bằng 2,5. Dung dịch nào có độ acid cao hơn và cao hơn bao nhiêu lần?

b) Nước cất có nồng dộ H⁺ là 10⁻⁷ mol/L. Nước chảy ra từ một vòi nước có độ pH từ 6,5 đến 6,7 thì có độ acid cao hay thấp hơn nước cất?

-----------------------------

Bài tiếp theo: Toán 11 Chân trời sáng tạo bài 1: Đạo hàm

Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Toán 11 Chân trời sáng tạo bài tập cuối chương 6: Hàm số và hàm số Lôgarit. Hi vọng qua bài viết này bạn đọc có thêm tài liệu để học tập tốt hơn môn Toán 11 Chân trời sáng tạo. Mời các bạn cùng tham khảo thêm tại mục Ngữ văn 11 Chân trời sáng tạo.

Chia sẻ, đánh giá bài viết

1

127

Bài trước

Bài sau