Toán 11 Chân trời sáng tạo bài tập cuối chương 8

Quan hệ vuông góc trong không gian

1 32

Toán 11 Chân trời sáng tạo bài tập cuối chương 8: Quan hệ vuông góc trong không gian

Bài 1 trang 86 SGK Toán 11 Chân trời
Bài 2 trang 86 SGK Toán 11 Chân trời
Bài 3 trang 86 SGK Toán 11 Chân trời
Bài 4 trang 86 SGK Toán 11 Chân trời
Bài 5 trang 86 SGK Toán 11 Chân trời
Bài 6 trang 86 SGK Toán 11 Chân trời
Bài 7 trang 86 SGK Toán 11 Chân trời
Bài 8 trang 86 SGK Toán 11 Chân trời
Bài 9 trang 86 SGK Toán 11 Chân trời
Bài 10 trang 87 SGK Toán 11 Chân trời
Bài 11 trang 87 SGK Toán 11 Chân trời
Bài 12 trang 87 SGK Toán 11 Chân trời
Bài 13 trang 87 SGK Toán 11 Chân trời

Toán 11 Chân trời sáng tạo bài tập cuối chương 8: Quan hệ vuông góc trong không gian được VnDoc.com sưu tầm và xin gửi tới bạn đọc cùng tham khảo. Mời các bạn cùng theo dõi để có thêm tài liệu giải bài tập Toán 11 Chân trời sáng tạo nhé.

Bài 1 trang 86 SGK Toán 11 Chân trời

Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc với mặt đáy. Đường thẳng CD vuông góc với mặt phẳng nào sau đây?

A. (SAD)

B. (SAC)

C. (SAB)

D. (SBD)

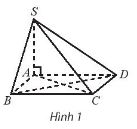
Toán 11 Chân trời sáng tạo bài tập cuối chương 8

Bài làm

Vì SA ⊥ (ABCD) nên SA ⊥ CD

Mà CD ⊥ AD nên CD ⊥ (SAD)

Đáp án: A

Bài 2 trang 86 SGK Toán 11 Chân trời

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh b, SA vuông góc với mặt đáy, SC = $2b\sqrt{2}$ . Số đo góc giữa cạnh bên SC và mặt đáy là:

A. 60^o

B. 30^o

C. 45^o

D. 50^o

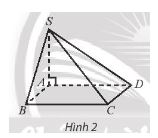
Bài làm

Đáp án A

Bài 3 trang 86 SGK Toán 11 Chân trời

Cho hình chóp S.ABCD có các cạnh bên và cạnh đáy đều bằng a. Gọi M là trung điểm của SA. Mặt phẳng (MBD) vuông góc với mặt phẳng nào dưới đây?

A. (SBC)

B. (SAC)

C. (SBD)

D. (ABCD)

Bài làm

Đáp án B

Bài 4 trang 86 SGK Toán 11 Chân trời

Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 2a và chiều cao bằng $a\sqrt{2}$ . Khoảng cách từ tâm O của đáy ABC đến một mặt bên là:

A. $\frac{a\sqrt{14}}{7}$

B. $\frac{a\sqrt{2}}{7}$

C. $\frac{a\sqrt{14}}{2}$

D. $\frac{2a\sqrt{14}}{7}$

Bài làm

Đáp án A

Bài 5 trang 86 SGK Toán 11 Chân trời

Thể tích của khối chóp cụt tam giác đều có cạnh đáy lớn bằng 2a, cạnh đáy nhỏ bằng a và chiều cao bằng $\frac{a\sqrt{6}}{3}$ là:

A. $\frac{7\sqrt{2}}{8}a^{3}$

B. $\frac{\sqrt{2}}{4}a^{3}$

C. $\frac{7\sqrt{2}}{12}a^{3}$

D. $\frac{7\sqrt{3}}{4}a^{3}$

Bài làm

Đáp án C

Bài 6 trang 86 SGK Toán 11 Chân trời

Cho chóp tứ giác S.ABCD có đáy là hình chữ nhật với AB = 4a, AD = 3a. Các cạnh bên đều có độ dài 5a. Góc nhị diện [S,BC,A] có số đo là:

A. 75^o46′

B. 71^o21′

C. 68^o31′

D. 65^o12′

Bài làm

Đáp án D

Bài 7 trang 86 SGK Toán 11 Chân trời

Nếu hình hộp chữ nhật có ba kích thước là 3;4;5 thì độ dài đường chéo của nó là:

A. $5\sqrt{2}$

B. 50

C. $2\sqrt{5}$

D. 12

Bài làm

Đáp án A

Bài 8 trang 86 SGK Toán 11 Chân trời

Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng a là:

A. $\frac{a^{3}.\sqrt{3}}{4}$

B. $\frac{a^{3}.\sqrt{3}}{3}$

C. $\frac{a^{3}.\sqrt{2}}{3}$

D. $\frac{a^{3}.\sqrt{2}}{2}$

Bài làm

Đáp án A

Bài 9 trang 86 SGK Toán 11 Chân trời

Cho hình vuông ABCD và tam giác đều SAB cạnh a nằm trong hai mặt phẳng vuông góc với nhau. Gọi M, N lần lượt là trung điểm của AB và AD.

a) Chứng minh rằng (SMD) ⊥ (SNC)

b) Tính khoảng cách từ M đến mặt phẳng (SNC)

Bài làm

a) Tam giác SAB đều có M là trung điểm AB nên SM\perp AB . Mà (SAB) $\perp$ (ABCD) nên SM $\perp$ (ABCD)

Suy ra: SM $\perp$ NC

Ta có tam giác AMD và tam giác DNC bằng nhau nên $\widehat{AMD}=\widehat{CND}$

mà $\widehat{AMD}+\widehat{ADM} = 90^{o}$ nên $\widehat{CND}+\widehat{ADM} = 90^{o}$

suy ra tam giác DNE vuông tại E. Hay DM $\perp$ NC

Mà SM $\perp$ NC nên NC $\perp$ (SMD)

Vậy (SNC) $\perp$ (SMD)

b) Kẻ MK $\perp$ (SE)

Vì NC $\perp$ (SMD) nên NC $\perp$ MK . Suy ra MK $\perp$ (SNC)

Tam giác SAB đều có SM là trung tuyến nên SM = $\frac{a\sqrt{3}}{2}$

Tam giác CND vuông có DE là đường cao nên $\frac{1}{DE^{2}}=\frac{1}{DN^{2}}+\frac{1}{DC^{2}}$ . Suy ra DE = $\frac{a\sqrt{5}}{5}$

DM = $\sqrt{AM^{2}+AD^{2}} = \frac{a\sqrt{5}}{2}$

ME = MD - DE = $\frac{3a\sqrt{5}}{10}$

SM $\perp$ (ABCD) nên SM $\perp$ ME

Tam giác SME vuông tại M có MK là đường cao nên $\frac{1}{MK^{2}}=\frac{1}{SM^{2}}+\frac{1}{ME^{2}}$ . Suy ra MK = $\frac{3a\sqrt{2}}{8}$

Bài 10 trang 87 SGK Toán 11 Chân trời

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA ⊥ (SABCD) và SA = a. Gọi M, N, P lần lượt là trung điểm của SB, SC và SD. Tính khoảng cách giữa AM và NP

Bài làm

SA ⊥ (SBCD) nên SA ⊥ BC

Mà BC ⊥ AB nên BC ⊥ (SAB)

Tam giác SBC có MN là đường trung bình nên MN // BC, MN = $\frac{1}{2}$ BC = $\frac{a}{2}$

Suy ra: MN ⊥ (SAB) và MN ⊥ AM

Tam giác SCD có NP là đường trung bình nên NP // CD

Mà MN // BC, BC ⊥ CD

Suy ra MN ⊥ NP

Vậy d(AM,NP) = MN = $\frac{a}{2}$

Bài 11 trang 87 SGK Toán 11 Chân trời

Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB = AD = 2a, CD = a; số đo góc nhị diện [S, BC, A] bằng 60^o. Gọi I là trung điểm của cạnh AD. Biết hai mặt phẳng (SBI) và (SCI) cùng vuông góc với mặt phẳng (ABCD). Tính thể tích khối chóp S.ABCD theo a.

Bài 12 trang 87 SGK Toán 11 Chân trời

Một chân cột bằng gang có dạng hình chóp cụt tứ giác đều có cạnh dáy lớn bằng 2a, cạnh đáy nhỏ bằng a, chiều cao h = 2a và bán kính đáy phần trụ rỗng bên trong bằng $\frac{a}{2}$

a) Tìm góc phẳng nhị diện tạo bởi mặt bên và mặt đáy

b) Tính thể tích chân cột nói trên theo a

Bài 13 trang 87 SGK Toán 11 Chân trời

Cho hình hộp ABCD.A'B'C'D' có cạnh bên AA' = a, đáy ABCD là hình thoi có AB = BD = a. Hình chiếu vuông góc của A' lên mặt đáy trùng với điểm O là giao điểm hai đường chéo của đáy. Tính thể tích của khối chóp.

----------------------------------

Bài tiếp theo: Toán 11 Chân trời sáng tạo bài 1: Biến cố giao và quy tắc nhân xác suất

Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Toán 11 Chân trời sáng tạo bài tập cuối chương 8: Quan hệ vuông góc trong không gian. Mong rằng qua bài viết này bạn đọc có thêm tài liệu để học tập tốt hơn môn Toán 11 Chân trời sáng tạo. Mời các bạn cùng tham khảo thêm tại mục Ngữ văn 11 Chân trời sáng tạo.

Đánh giá bài viết

1 32

Bài trước

Bài sau