Toán 11 Chân trời sáng tạo bài 1

Góc lượng giác

Toán 11 Chân trời sáng tạo bài 1: Góc lượng giác

Bài 1 trang 12 SGK Toán 11 Chân trời sáng tạo
Bài 2 trang 12 SGK Toán 11 Chân trời sáng tạo
Bài 3 trang 12 SGK Toán 11 Chân trời sáng tạo
Bài 4 trang 12 SGK Toán 11 Chân trời sáng tạo
Bài 5 trang 12 SGK Toán 11 Chân trời sáng tạo
Bài 6 trang 12 SGK Toán 11 Chân trời sáng tạo
Bài 7 trang 13 SGK Toán 11 Chân trời sáng tạo
Bài 8 trang 13 SGK Toán 11 Chân trời sáng tạo
Bài 9 trang 13 SGK Toán 11 Chân trời sáng tạo

Toán 11 Chân trời sáng tạo bài 1 Góc lượng giác được VnDoc.com sưu tầm và xin gửi tới bạn đọc cùng tham khảo. Mong rằng qua bài viết này bạn đọc có thêm tài liệu để giải bài tập Toán 11 Chân trời sáng tạo nhé. Mời các bạn cùng theo dõi bài viết.

Bài 1 trang 12 SGK Toán 11 Chân trời sáng tạo

Đổi số đo của các góc sau đây sang radian:

a) 38^o

b) -115^o

c) ( $\frac{3}{\pi }$ $\frac{3}{\pi }$)^o

Lời giải

a) $38^{o} = \frac{19\pi }{90}$ $38^{o} = \frac{19\pi }{90}$ rad

b) $-115^{o} = - \frac{23\pi }{36}$ $-115^{o} = - \frac{23\pi }{36}$ rad

c) $\left ( \frac{3}{\pi } \right )^{o} = \frac{1}{60}$ $\left ( \frac{3}{\pi } \right )^{o} = \frac{1}{60}$ rad

Bài 2 trang 12 SGK Toán 11 Chân trời sáng tạo

Đổi số đo của các góc sau đây sang độ:

a) $\frac{\pi }{12}$ $\frac{\pi }{12}$

b) -5

c) $\frac{13\pi }{9}$ $\frac{13\pi }{9}$

Lời giải

$\frac{\pi }{12} = 15^{o}$ $\frac{\pi }{12} = 15^{o}$

$-5 = - 286,5^{o}$ $-5 = - 286,5^{o}$

$\frac{13\pi }{9} = 260^{o}$ $\frac{13\pi }{9} = 260^{o}$

Bài 3 trang 12 SGK Toán 11 Chân trời sáng tạo

Biểu diễn các góc lượng giác sau trên đường tròn lượng giác

a) $\frac{-17\pi }{3}$ $\frac{-17\pi }{3}$

b) $\frac{13\pi }{4}$ $\frac{13\pi }{4}$

c) $-765^{o}$ $-765^{o}$

Lời giải

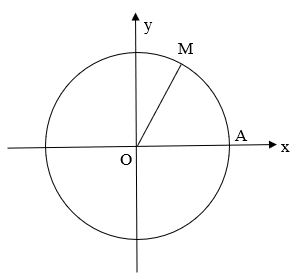
a) Ta có $\frac{-17\pi }{3} = \frac{\pi }{3} - 3.2\pi$ $\frac{-17\pi }{3} = \frac{\pi }{3} - 3.2\pi$. Vậy điểm biểu diễn góc lượng giác có số đo $\frac{-17\pi }{3}$ $\frac{-17\pi }{3}$ là điểm M trên phần đường tròn lượng giác thuộc góc phần tư thứ I sao cho $\widehat{AOM} = \frac{\pi }{3}$ $\widehat{AOM} = \frac{\pi }{3}$

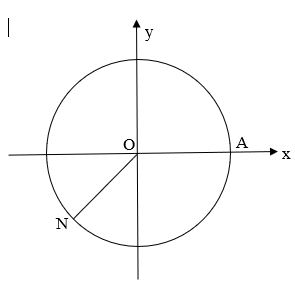
Toán 11 Chân trời sáng tạo bài 1 Góc lượng giác

b) Ta có $\frac{13\pi }{4} = \frac{5\pi }{4} + 2\pi$ $\frac{13\pi }{4} = \frac{5\pi }{4} + 2\pi$. Vậy điểm biểu diễn góc lượng giác có số đo $\frac{13\pi }{4}$ $\frac{13\pi }{4}$ là điểm N trên phần đường tròn lượng giác thuộc góc phần tư thứ III sao cho $\widehat{AON} = \frac{5\pi }{4}$ $\widehat{AON} = \frac{5\pi }{4}$

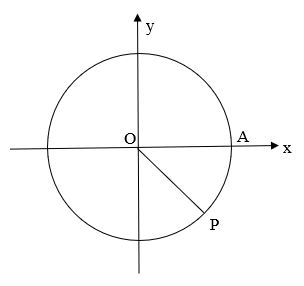
Toán 11 Chân trời sáng tạo bài 1 Góc lượng giác

Ta có $-765^{o} = -45^{o} - 2.360^{o}$ $-765^{o} = -45^{o} - 2.360^{o}$. Vậy điểm biểu diễn góc lượng giác có số đo $-765^{o}$ $-765^{o}$ là điểm P trên phần đường tròn lượng giác thuộc góc phần tư thứ IV sao cho $\widehat{AOP} = -45^{o}$ $\widehat{AOP} = -45^{o}$

Toán 11 Chân trời sáng tạo bài 1 Góc lượng giác

Bài 4 trang 12 SGK Toán 11 Chân trời sáng tạo

Góc lượng giác $\frac{31\pi }{7}$ $\frac{31\pi }{7}$ có cùng điểm biểu diễn trên đường tròn lượng giác với góc lượng giác nào sau đây?

$\frac{3\pi }{7} ; \frac{10\pi }{7} ; \frac{-25\pi }{7}$ $\frac{3\pi }{7} ; \frac{10\pi }{7} ; \frac{-25\pi }{7}$

Lời giải

Ta có:

$\frac{31\pi }{7} = \frac{3\pi }{7} + 2.2\pi$ $\frac{31\pi }{7} = \frac{3\pi }{7} + 2.2\pi$

$\frac{-25\pi }{7} = \frac{3\pi }{7} - 2.2\pi$ $\frac{-25\pi }{7} = \frac{3\pi }{7} - 2.2\pi$

Vậy góc lượng giác $\frac{31\pi }{7}$ $\frac{31\pi }{7}$ có cùng điểm biểu diễn với góc lượng giác $\frac{3\pi }{7} và \frac{-25\pi }{7}$ $\frac{3\pi }{7} và \frac{-25\pi }{7}$

Bài 5 trang 12 SGK Toán 11 Chân trời sáng tạo

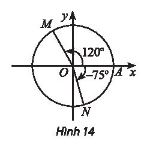
Viết công thức số đo tổng quát của các góc lượng giác (OA, OM) và (OA, ON) trong Hình 14

Toán 11 Chân trời sáng tạo bài 1 Góc lượng giác

Lời giải

(OA, OM) = $\frac{2\pi }{3} + k.2\pi$ $\frac{2\pi }{3} + k.2\pi$

(OA, ON) = $\frac{5\pi }{12} + k.2\pi$ $\frac{5\pi }{12} + k.2\pi$

Bài 6 trang 12 SGK Toán 11 Chân trời sáng tạo

Viết công thức số đo tổng quát của góc lượng giác (Ox, ON).

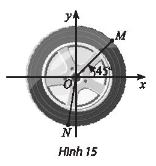
Toán 11 Chân trời sáng tạo bài 1 Góc lượng giác

Lời giải

(Ox, ON) = −99^o + k.360^o

Bài 7 trang 13 SGK Toán 11 Chân trời sáng tạo

Trên đường tròn lượng giác, hãy biểu diễn các góc lượng giác có số đo có dạng là:

a) $\frac{\pi }{2} + k\pi (k \epsilon \mathbb{Z})$ $\frac{\pi }{2} + k\pi (k \epsilon \mathbb{Z})$

b) $k\frac{\pi }{4} (k \epsilon \mathbb{Z})$ $k\frac{\pi }{4} (k \epsilon \mathbb{Z})$

Lời giải

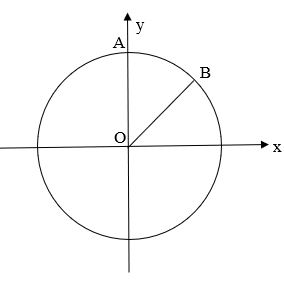
Góc lượng giác có số đo có dạng $\frac{\pi }{2} + k\pi (k\epsilon \mathbb{Z})$ $\frac{\pi }{2} + k\pi (k\epsilon \mathbb{Z})$ được biểu diễn bằng điểm A trên đường tròn lượng giác.

Góc lượng giác có số đo có dạng $k\frac{\pi }{4} (k \epsilon \mathbb{Z})$ $k\frac{\pi }{4} (k \epsilon \mathbb{Z})$ được biểu diễn bằng điểm B trên đường tròn lượng giác.

Toán 11 Chân trời sáng tạo bài 1 Góc lượng giác

Bài 8 trang 13 SGK Toán 11 Chân trời sáng tạo

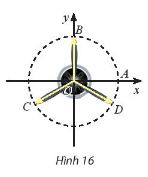
Vị trí các điểm B, C, D trên cánh quạt động cơ máy bay trong Hình 16 có thể được biểu diễn cho các góc lượng giác nào sau đây?

$\frac{\pi }{2} + k \frac{2\pi }{3} (k \epsilon \mathbb{Z}) ; \frac{-\pi }{6} + k \frac{2\pi }{3} (k \epsilon \mathbb{Z}) ; \frac{\pi }{3} + k \frac{\pi }{3} (k \epsilon \mathbb{Z})$ $\frac{\pi }{2} + k \frac{2\pi }{3} (k \epsilon \mathbb{Z}) ; \frac{-\pi }{6} + k \frac{2\pi }{3} (k \epsilon \mathbb{Z}) ; \frac{\pi }{3} + k \frac{\pi }{3} (k \epsilon \mathbb{Z})$

Toán 11 Chân trời sáng tạo bài 1 Góc lượng giác

Lời giải

Điểm B, C, D biểu diễn cho góc lượng giác $\frac{\pi }{2} + k \frac{2\pi }{3} (k \epsilon \mathbb{Z})$ $\frac{\pi }{2} + k \frac{2\pi }{3} (k \epsilon \mathbb{Z})$

Bài 9 trang 13 SGK Toán 11 Chân trời sáng tạo

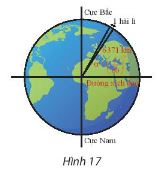
Hải li là một đơn vị chiều dài hàng hải, được tính bằng độ dài một cung chắn một góc α = ( $\frac{1}{60}$ $\frac{1}{60}$)^o của đường kinh tuyến (Hình 17). Đổi số đo α sang radian và cho biết 1 hải li bằng khoảng bao nhiêu kilômét, biết bán kính trung bình của Trái Đất là 6371km. Làm tròn kết quả đến hàng phần trăm.

Toán 11 Chân trời sáng tạo bài 1 Góc lượng giác

Lời giải

$\alpha = \left ( \frac{1}{60}\right )^{o} = \frac{\pi }{10800}$ $\alpha = \left ( \frac{1}{60}\right )^{o} = \frac{\pi }{10800}$ rad

1 hải li = $\frac{\pi }{10800} . 6371 \approx 1,85$ $\frac{\pi }{10800} . 6371 \approx 1,85$ (km)

-------------------------

Toán 11 Chân trời sáng tạo bài 1

VnDoc.com vừa gửi tới bạn đọc bài viết Toán 11 Chân trời sáng tạo bài 1 Góc lượng giác. Hi vọng qua đây bạn đọc có thêm tài liệu để học tập tốt hơn môn Toán 11 Chân trời sáng tạo. Mời các bạn cùng tham khảo thêm tại mục Ngữ văn 11 Chân trời sáng tạo.

Chia sẻ, đánh giá bài viết

1

834

Bài trước

Bài sau