Toán 11 Chân trời sáng tạo bài 3 trang 107

Toán 11 Chân trời sáng tạo bài 3: Đường thẳng và mặt phẳng song song được VnDoc.com sưu tầm và xin gửi tới bạn đọc cùng tham khảo. Hi vọng qua bài viết này bạn đọc có thêm tài liệu để giải bài tập Toán 11 Chân trời sáng tạo nhé. Mời các bạn cùng theo dõi bài viết dưới đây.

Bài 1 trang 111 SGK Toán 11 Chân trời

Cho hình chóp S.ABCD, đáy ABCD là hình bình hành có O là giao điểm hai đường chéo. Cho M là trung điểm SC.

a) Chứng minh đường thẳng OM song song với hai mặt phẳng (SAD) và (SBA)

b) Tìm giao tuyến của hai mặt phẳng (OMD) và (SAD)

Bài làm

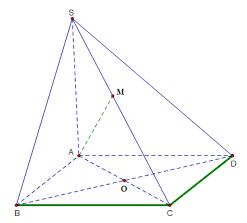
a) Trong tam giác SAC, O và M lần lượt là trung điểm của AC và SC nên OM//SA

Mà SA ⊂ (SAD); SA ⊂ (SBA)

Nên OM//(SAD), OM//(SBA)

b) Hai mặt phẳng (SAD) và (OMD) có SA//OM nên giao tuyến của hai mặt phẳng là đường thẳng đi qua D song song với SA và OM

Bài 2 trang 112 SGK Toán 11 Chân trời

Cho hai hình bình hành ABCD và ABEF không nằm trong cùng một mặt phẳng. Gọi O và O' lần lượt là tâm của ABCD và ABEF.

a) Chứng minh đường thẳng OO' song song với các mặt phẳng (CDEF), (ADF) và (BCE)

b) Gọi M và N lần lượt là trung điểm của AF và BE. Chứng minh MN//(CDFE)

c) Tìm giao tuyến của hai mặt phẳng (OMN) và (ABCD)

Bài làm

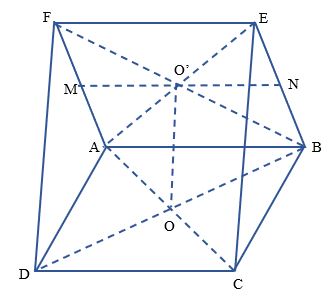
a) Trong tam giác FBD, O và O' lần lượt là trung điểm của BD và BF nên OO'//FD

Mà FD ⊂ (EFDC), FD ⊂ (ADF) nên OO'//(EFDC), OO'//(ADF)

Trong tam giác AEC, O và O' lần lượt là trung điểm của AE và AC nên OO'//EC

Mà EC ⊂ (BCE) nên OO'//(BCE)

b) Trong hình bình hành ABEF có M, N lần lượt là trung điểm của AE và BF nên MN//EF//AB

Mà EF ⊂ (CDFE) nên MN//(CDFE)

c) Hai mặt phẳng (OMN) và (ABCD) có điểm O chung, MN//AB nên giao tuyến của hai mặt phẳng là đường thẳng đi qua O và song song với AB

Bài 3 trang 112 SGK Toán 11 Chân trời

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và một điểm M di động trên cạnh AD. Một mặt phẳng (α) qua M, song song với CD và SA, cắt BC, SC, SD lần lượt tại N,P,Q.

a) MNPQ là hình gì?

b) Gọi I = MQ ∩ NP. Chứng minh rằng I luôn luôn thuộc một đường thẳng cố định khi M di động trên AD.

Bài làm

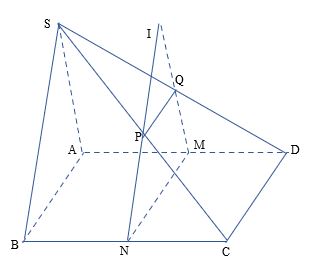
a) CD//(α), (SCD) chứa CD cắt (α) tại PQ nên PQ//CD

CD//(α), (ABCD) chứa CD cắt (α) tại MN nên MN//CD

Suy ra: MN//PQ

b) Mặt phẳng (SBC) và (SAD) giao nhau tại đường thẳng đi qua S và song song với BC và AD

I ∈ NP, NP ⊂ (SBC) nên I ∈ (SBC)

I ∈ QM, QM ⊂ (SAD) nên I ∈ (SAD)

Do đó I là điểm chung của hai mặt phẳng (SBC) và (SAD) nên I nằm trên giao tuyến của hai mặt phẳng đó

Suy ra I nằm trên đường thẳng đi qua S và song song với BC

Bài 4 trang 112 SGK Toán 11 Chân trời

Cho tứ diện ABCD và điểm M thuộc cạnh AB. Gọi (α) là mặt phẳng qua M, song song với hai đường thẳng BC và AD. Gọi N, P, Q lần lượt là giao điểm của mặt phẳng (α) với các cạnh AC, CD và BD.

a) Chứng minh MNPQ là hình bình hành

b) Trong trường hợp nào thì MNPQ là hình thoi?

Bài làm

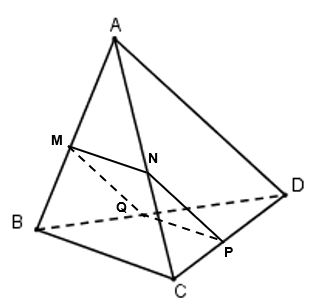
a) (α) // BC, BC ⊂ (ABC) và (α) cắt (ABC) tại MN nên MN // BC

(α) // BC, BC ⊂ (BCD) và (α) cắt (BCD) tại PQ nên PQ // BC

Suy ra: MN//PQ

(α) // AD, AD ⊂ (ABD) và (α) cắt (ABD) tại MQ nên MQ // AD

(α) // AD, AD ⊂ (ACD) và (α) cắt (ACD) tại NP nên NP // BC

Suy ra: MQ//NP

Do đó, MNPQ là hình bình hành

b) MNPQ là hình thoi khi MN = NP

Ta có: \(\frac{MN}{BC}\) = \(\frac{AN}{AC}\)

\(\frac{NP}{AD}\) = \(\frac{CN}{AC}\) hay \(\frac{MN}{AD}\) =  \(\frac{CN}{AC}\)

Mà \(\frac{AN}{AC}\) + \(\frac{CN}{AC}\) = 1 nên \(\frac{MN}{BC}\) + \(\frac{MN}{AD}\) = 1

Suy ra: MN = \(\frac{AD.BC}{AD+BC}\)

Bài 5 trang 112 SGK Toán 11 Chân trời

Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AB. Gọi M là trung điểm của CD, (P) là mặt phẳng qua M song song với SA và BC. Tìm giao tuyến của (P) với các mặt của hình chóp S.ABCD.

Bài làm

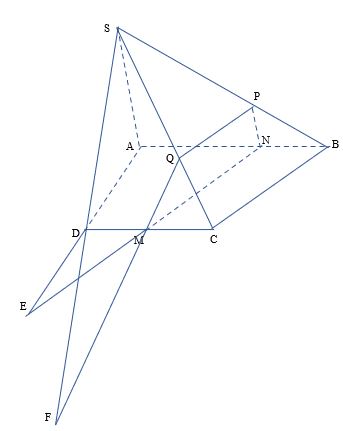
Qua M kẻ đường thẳng song song với BC cắt AB tại N

Qua N kẻ đường thẳng song song với SA cắt AB tại P

Qua P kẻ đường thẳng song song với BC cắt SC tại Q

Mặt phẳng (MNPQ) có MN//SB, NP//SA nên mặt phẳng (MNPQ) là mặt phẳng (P)

Giao tuyến của (P) với (ABCD), (SAB), (SBC), (SCD) lần lượt là MN, NP, PQ và QM

Trong mặt phẳng (ABCD), gọi E là giao điểm của MN và AD

Trong mặt phẳng (ACD), gọi F là giao điểm của MQ và SD

Ta có: E và F là hai điểm chung của mặt phẳng (P) và (SAD) nên giao tuyến của (P) với (SAD) là EF

Bài 6 trang 112 SGK Toán 11 Chân trời

Mô tả vị trí tương đối của các đường thẳng a, b, c, d, e với mặt phẳng (P) là mặt trước của toà nhà (Hình 19).

Bài làm

Đường thẳng a, e nằm trong mặt phẳng (P)

Đường thẳng b, c song song với mặt phẳng (P)

Đường thẳng d cắt mặt phẳng (P)

--------------------------

Bài tiếp theo: Toán 11 Chân trời sáng tạo bài 4 trang 113

Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Toán 11 Chân trời sáng tạo bài 3: Đường thẳng và mặt phẳng song song. Mong rằng qua bài viết này bạn đọc có thêm tài liệu để học tập tốt hơn môn Toán 11 Chân trời sáng tạo. Mời các bạn cùng tham khảo thêm tại mục Ngữ văn 11 Chân trời sáng tạo, Vật lý 11 Chân trời sáng tạo.