Toán 11 Chân trời sáng tạo bài 2 trang 56
Toán 11 Chân trời sáng tạo bài 2: Đường thẳng vuông góc với mặt phẳng
Toán 11 Chân trời sáng tạo bài 2: Đường thẳng vuông góc với mặt phẳng được VnDoc.com sưu tầm và xin gửi tới bạn đọc cùng tham khảo để có thêm tài liệu giải bài tập Toán 11 Chân trời sáng tạo nhé.
Bài 1 trang 64 SGK Toán 11 Chân trời
Cho hình chóp S.ABCD có SA ⊥ (ABCD). Cho biết ABCD là hình thang vuông tại A và D, AB = 2AD
a) Chứng minh CD ⊥ (SAD)
b) Gọi M là trung điểm của AB. Chứng minh CM ⊥ (SAB)
Bài làm
a) Vì SA ⊥ (ABCD) nên SA ⊥ CD
Ta có: DC ⊥ AD; DC ⊥ SA nên DC ⊥ (SAD)
b) Vì SA ⊥ (ABCD) nên SA ⊥ CM
Ta có: AB = 2CD nên AM = CD. Suy ra AMCD là hình chữ nhật nên CM ⊥ AB
Mà CM ⊥ SA
Suy ra: CM ⊥ (SAB)
Bài 2 trang 64 SGK Toán 11 Chân trời
Cho hình vuông ABCD. Gọi H, K lần lượt là trung điểm của AB, AD. Trên đường thẳng vuông góc với (ABCD) tại H, lấy điểm S. Chứng minh rằng:
a) AC ⊥ (SHK)
b) CK ⊥ (SDH)
Bài làm
a) Tam giác ABD có HK là đường trung bình nên HK // BD
Vì ABCD là hình vuông nên AC ⊥ BD. Suy ra AC ⊥ HK
Vì SH ⊥ (ABCD) nên SH ⊥ AC
Ta có: AC ⊥ SH, AC ⊥ HK nên AC ⊥ (SHK)
b) Ta có tam giác AHD và tam giác DKC bằng nhau nên DH ⊥ CK
Mà SH ⊥ (ABCD) nên SH ⊥ CK
Suy ra CK ⊥ (SDH)
Bài 3 trang 64 SGK Toán 11 Chân trời
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng a
\(\sqrt{2}\), có các cạnh bên đều bằng 2a
a) Tính góc giữa SC và AB
b) Tính diện tích hình chiếu vuông góc của tam giác SAB trên mặt phẳng (ABCD)
Bài làm
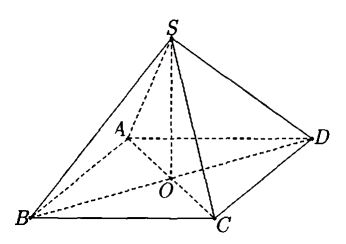
a) AB // CD nên góc giữa SC và AB là góc giữa SC và CD:\(\widehat{SCD}\)
\(cos\widehat{SCD} =\frac{(2a)^{2}+a^{2}-(2a)^{2}}{2.2a.a}=\frac{1}{4}\)
Suy ra \(\widehat{SCD} =75,5^{o}\)
b) Kẻ SO \(\perp\) (ABCD) . Do các cạnh bên của hình chóp bằng nhau nên O là tâm của hình vuông ABCD.
Ta có: AO \(\perp\) OB; AC =\(\sqrt{2}.\sqrt{2}.a=2a\); AO = BO = \(\frac{1}{2}.2a=a\)
Hình chiếu vuông góc của tam giác SAB là tam giác OAB có diện tích là \(\frac{1}{2}.a.a=\frac{1}{2}.a^{2}\)
Bài 4 trang 64 SGK Toán 11 Chân trời
Cho hình chóp S.ABC có SA = SB = SC = a, \(\widehat{ASB} = 90^{o}\); \(\widehat{BSC} = 60^{o}\) và \(\widehat{ASC} = 120^{o}\). Gọi I là trung điểm cạnh AC. Chứng minh SI \(\perp\) (ABC)
Bài 5 trang 64 SGK Toán 11 Chân trời
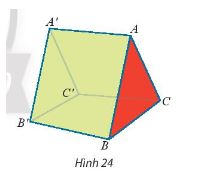
Một cái lều có dạng hình lăng trụ ABC.A'B'C' có cạnh bên AA' vuông góc với đáy (Hình 24)
Cho biết AB = AC = 2,4m; BC = 2m; AA' = 3m
a) Tính góc giữa hai đường thẳng AA' và BC; A'B' và AC
b) Tính diện tích hình chiếu vuông góc của tam giác ABB' trên mặt phẳng (BB'C'C)
-----------------------------------
Bài tiếp theo: Toán 11 Chân trời sáng tạo bài 3: Hai mặt phẳng vuông góc
Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Toán 11 Chân trời sáng tạo bài 2: Đường thẳng vuông góc với mặt phẳng. Hi vọng qua bài viết này bạn đọc có thêm tài liệu để học tập tốt hơn môn Toán 11 Chân trời sáng tạo. Mời các bạn cùng tham khảo thêm tại mục Ngữ văn 11 Chân trời sáng tạo.
