Toán 11 Kết nối tri thức bài Ôn tập cuối năm

Toán 11 Kết nối

1 93

Toán 11 Kết nối bài Ôn tập cuối năm

Bài 1 trang 105 SGK Toán 11 Kết nối
Bài 2 trang 105 SGK Toán 11 Kết nối
Bài 3 trang 105 SGK Toán 11 Kết nối
Bài 4 trang 105 SGK Toán 11 Kết nối
Bài 5 trang 105 SGK Toán 11 Kết nối
Bài 6 trang 105 SGK Toán 11 Kết nối
Bài 7 trang 105 SGK Toán 11 Kết nối
Bài 8 trang 105 SGK Toán 11 Kết nối
Bài 9 trang 106 SGK Toán 11 Kết nối
Bài 10 trang 106 SGK Toán 11 Kết nối
Bài 11 trang 106 SGK Toán 11 Kết nối
Bài 12 trang 106 SGK Toán 11 Kết nối
Bài 13 trang 106 SGK Toán 11 Kết nối
Bài 14 trang 106 SGK Toán 11 Kết nối
Bài 15 trang 106 SGK Toán 11 Kết nối
Bài 16 trang 106 SGK Toán 11 Kết nối
Bài 17 trang 106 SGK Toán 11 Kết nối
Bài 18 trang 106 SGK Toán 11 Kết nối
Bài 19 trang 107 SGK Toán 11 Kết nối
Bài 20 trang 107 SGK Toán 11 Kết nối
Bài 21 trang 107 SGK Toán 11 Kết nối
Bài 22 trang 107 SGK Toán 11 Kết nối

VnDoc.com xin gửi tới bạn đọc bài viết Toán 11 Kết nối tri thức bài Ôn tập cuối năm để bạn đọc cùng tham khảo. Hi vọng qua đây bạn đọc có thêm tài liệu để giải bài tập Toán 11 Kết nối tri thức. Mời các bạn cùng theo dõi bài viết dưới đây nhé.

Bài 1 trang 105 SGK Toán 11 Kết nối

Khẳng định nào sau đây sai?

A. cos(α + β) = cosαcosβ + sinαsinβ

B. sin(α + β) = sinαcosβ + cosαsinβ

C. sin( $\frac{\pi }{2}$ + a) = cosα

D. cos2α = cos²α − sin²α

Bài làm

Đáp án C

Bài 2 trang 105 SGK Toán 11 Kết nối

Khẳng định nào sau đây đúng?

A. Hàm số y = sinx tuần hoàn với chu kì π.

B. Hàm số y = cosx tuần hoàn với chu kì 2π

C. Hàm số y = tanx tuần hoàn với chu kì 2π

D. Hàm số y = cotx tuần hoàn với chu kỉ 2π

Bài làm

Đáp án B

Bài 3 trang 105 SGK Toán 11 Kết nối

Cho biết dãy số (U_n) với U_n = 5ⁿ. Số hạng U_2n bằng

A. 2.5ⁿ

B. 25ⁿ

C. 10ⁿ

D. $5^{n^{2} }$

Bài làm

Đáp án B

Bài 4 trang 105 SGK Toán 11 Kết nối

Hãy cho biết dãy số $(U_{n})$ nào dưới dây là dãy số tăng, nếu biết công thức só hạn tộng quát của nó là

A. $\frac{1}{n^{2}+1}$

B. $2^{-n}$

C. $\log_{\frac{1}{2}}n$

D. $\frac{n}{n+1}$

Bài làm

Đáp án D

Bài 5 trang 105 SGK Toán 11 Kết nối

Khẳng định nào sau đây là sai?

A. Nếu $\lim_{x \rightarrow x_{0}} f(x)= L \geq 0$ thì $\lim_{x\rightarrow x_{0}}\sqrt{f(x)}=\sqrt{L}$

B. $\lim_{x\rightarrow x_{0}} \frac{1}{x} = -\infty$

C. Nếu $|q| \leq 1$ thì $\lim_{n\rightarrow +\infty} q^{n} = 0$

D. $\lim_{n\rightarrow +\infty}\frac{sin n}{n+1}=0$

Bài làm

Đáp án B

Bài 6 trang 105 SGK Toán 11 Kết nối

Hàm số nào dưới đây không liên tục trên $\mathbb{R}$ ?

A. y = tan x

B. $y=\frac{2x^{2}3x-1}{x^{2}+1}$

C. y = sinx

D. y =|x|

Bài làm

Đáp án D

Bài 7 trang 105 SGK Toán 11 Kết nối

Cho $0< a\neq 1$ . Giá trị của biểu thức $\log_{a}(a^{3} . \sqrt[4]{a}) + (\sqrt[3]{a})^{\log_{a}8}$ bằng

A. $\frac{19}{4}$

B. 9

C. $\frac{21}{4}$

D. $\frac{47}{12}$

Bài làm

Đáp án C

Bài 8 trang 105 SGK Toán 11 Kết nối

Cho đồ thị ba hàm số mũ y = a^x, y = b^xvà y = c^x như trong hinh vẽ dưới đây. Khẳng định nào đúng?

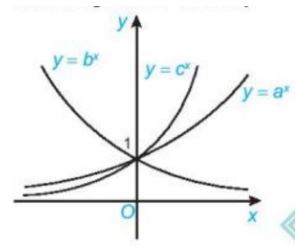
Toán 11 Kết nối tri thức bài Ôn tập cuối năm

A. a > c > b

B. b > a > c

C. c > a > b

D. c > b > a

Bài làm

Đáp án C

Bài 9 trang 106 SGK Toán 11 Kết nối

Nếu f(x) = sin²x + xe^2x thì f"(0) bằng

A. 4

B. 5

C. 6

D. 0

Bài làm

Đáp án A

Bài 10 trang 106 SGK Toán 11 Kết nối

Phương trình tiếp tuyến của đồ thị hàm số y = −2x³ + 6x² − 5 tại điểm M(3; -5) thuộc đồ thị là

A. y = 18x + 49

B. y = 18x - 49

C. y = -18x - 49

D. y = -18x + 49

Bài làm

Đáp án D

Bài 11 trang 106 SGK Toán 11 Kết nối

Cho hình hộp S.ABC có đáy ABC là tam giác đều cạnh a và SA $\perp$ (ABC), SA = $a \sqrt{2}$ . Khoảng cách từ A đến mặt phẳng (SBC) bằng

A. $\frac{6a}{11}$

B. $\frac{a \sqrt{66}}{11}$

C. $\frac{a\sqrt{6}}{11}$

D. $\frac{a\sqrt{11}}{11}$

Bài làm

Đáp án D

Bài 12 trang 106 SGK Toán 11 Kết nối

Cho hình hộp ABCD.A'B'C'D' có đáy ABCD là hình chữ nhật. Biết AC = AA' = 2a. Giá trị lớn nhất của thể tích hình hộp ABCD.A'B'C'D' bằng

A. 8a³

B. 6a³

C. 4a³

D. a³

Bài làm

Đáp án C

Bài 13 trang 106 SGK Toán 11 Kết nối

Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của cạnh AC và cạnh AD. Thể tích khối chóp B.CMND bằng

A. $\frac{a^{3} \sqrt{2}}{12}$

B. $\frac{a^{3} \sqrt{2}}{16}$

C. $\frac{a^{3} \sqrt{2}}{24}$

D. $\frac{a^{3} \sqrt{2}}{8}$

Bài làm

Đáp án C

Bài 14 trang 106 SGK Toán 11 Kết nối

Cho lăng trụ tam giác đều ABC.A'B'C' có AB = 1 AA' = 2. Thể tích khối lăng trụ ABC.A'B'C bằng

A. $\frac{\sqrt{3}}{2}$

B. $\frac{\sqrt{3}}{6}$

C. $\frac{\sqrt{3}}{4}$

D. $\frac{\sqrt{3}}{8}$

Bài làm

Đáp án B

Bài 15 trang 106 SGK Toán 11 Kết nối

Cho hình lập phương ABCD.A'B'C'D' có AC' = $\sqrt{3}$ . Khoảng cách giữa hai đường thẳng AB' và BC' bằng

A. $\frac{1}{3}$

B. $\frac{\sqrt{3}}{3}$

C. $\frac{\sqrt{3}}{2}$

D. $\frac{1}{2}$

Bài làm

Đáp án C

Bài 16 trang 106 SGK Toán 11 Kết nối

Toán 11 Kết nối tri thức bài Ôn tập cuối năm

Nhóm chứa trung vị là:

A. [5;10)

B. [10;15)

C. [15;20)

D. [20; 25)

Bài làm

Đáp án C

Bài 17 trang 106 SGK Toán 11 Kết nối

Toán 11 Kết nối tri thức bài Ôn tập cuối năm

Nhóm chứa mốt là:

A. [5;10)

B. [10;15)

C. [15;20)

D. [20; 25)

Bài làm

Đáp án C

Bài 18 trang 106 SGK Toán 11 Kết nối

Vận động viên Tùng thi bắn súng. Biết rằng xác suất để Tùng bắn trúng vòng 10 là 0,2. Mỗi vận động viên được bắn hai lần và hai lần bắn là độc lập. Vận động viên đạt huy chương vàng nếu cả hai lần bắn trúng vòng 10. Xác suất để vận động viên Tùng đạt huy chương vàng là

A. 0,04

B. 0,035

C. 0,05

D. 0,045

Bài làm

Đáp án A

Bài 19 trang 107 SGK Toán 11 Kết nối

Hai bạn Sơn và Tùng, mỗi người gieo một con xúc xắc. Xác suất để số chấm xuất hiện trên cả hai con xúc xắc của Sơn và Tùng lớn hơn 1 là

A. $\frac{27}{36}$

B. $\frac{25}{36}$

C. $\frac{26}{35}$

D. $\frac{28}{37}$

Bài làm

Đáp án B

Bài 20 trang 107 SGK Toán 11 Kết nối

Hai bạn An và Bình tham gia một trò chơi độc lập với nhau. Xác suất để An và Bình giành giải thưởng tương ứng là 0,8 và 0,6. Xác suất đề có ít nhất một bạn giành giải thưởng là

A. 0,94

B. 0,924

C. 0,92

D. 0,93

Bài làm

Đáp án C

Bài 21 trang 107 SGK Toán 11 Kết nối

Rút gọn các biểu thức sau:

a) $A=\frac{1-2sin^{2}x}{1+sin^{2}2x} - \frac{1-tan x}{1+tan x}$

b) $B=\frac{sin 4x}{1+cos 4x}.\frac{cos2x}{1+cos2x}- cot(frac{3 \pi}{2} - x)$

c) $C = 2(cos^{4} x - sin ^{4} x) sin2x$

Bài làm

a) $A=\frac{1-2sin^{2}x}{1+sin^{2}2x} - \frac{1-tan x}{1+tan x}$

$= \frac{1-2sin^{2}x}{cos^{2}2x+sin^{2}2x.sin^{2}x} - \frac{cosx-sinx}{cosx+sinx}$

$=\frac{(cos^2 2x + sin^2 2x.sin^2 x)(1-2sin^2 x)}{(cos^2 2x + sin^2 2x.sin^2 x)}-\frac{(cosx-sinx)^2}{(cosx+sinx)(cosx-sinx)}$

$=\frac{cos^2 2x + sin^2 2x.sin^2 x - 2sin^2 x - cos^2 x - sin^2 x + 2cosx sinx}{cos^2 2x + sin^2 2x.sin^2 x}$

$= \frac{cos^2 2x - cos^2 x + 2sin^2 x - sin^2 x + 2cosx sinx}{cos^2 2x + sin^2 2x.sin^2 x}$

$= \frac{cos^2 x (2cos^2 x - cos^2 2x + 2sin^2 x) + sin^2 x (2cosx sinx)}{cos^2 2x + sin^2 2x.sin^2 x}$

$= \frac{cos^2 x (2 - 2sin^2 x) + sin^2 x (sin2x)}{cos^2 2x + sin^2 2x.sin^2 x}$

$= \frac{2cos^2 x - 2cos^2 x sin^2 x + sin^2 x sin2x}{cos^2 2x + sin^2 2x.sin^2 x} = \frac{2cos^2 x (1-sin^2 x) + sin^2 x sin2x}{cos^2 2x + sin^2 2x.sin^2 x}$

$= \frac{2cos^2 x cos^2 x + sin^2 x sin2x}{cos^2 2x + sin^2 2x.sin^2 x}$

$= \frac{cos^2 x(2cos^2 x + sin^2 2x)}{cos^2 2x + sin^2 2x.sin^2 x}$

$= \frac{cos^2 x}{1+sin^2 2x}$

b)

$B = \frac{sin 4x}{1+cos 4x}.\frac{cos2x}{1+cos2x}- cot(\frac{3 \pi}{2} - x)$

$= \frac{2sin2x cos2x}{2cos^2 2x}.\frac{cos2x}{1+cos2x} + tanx$

$= \frac{sin 2x}{cos^2 2x}. \frac{cos2x}{1+cos2x} + tanx$

$= \frac{2sinx cosx}{(1+cos2x)(1-cos2x)}.\frac{1+cos2x}{2} + tanx$

$= \frac{sinx}{cos^2 x} + tanx$

$= \frac{sin^2 x}{sin x cos^2 x} + \frac{sinx}{cosx}$

$= \frac{1}{cos^2 x} + \frac{sinx}{cosx}$

$= sec^2 x + tanx$

c)

$C= 2( cos^{4}x - sin^{4}x)sin2x$

$= 2cos^{4}xsin2x - 2sin^{4}x.sin2x$

$= 2cos^{4}xsin2x - 2sin^{2}x(1-cos^{2}x)sin2x$

$=2cos^{2}x(cos^{2}x-sin^{2}x)sin2x$

$=2cos^{2}x.cos2x.sin2x$

$=4cos^{2}x.cos2xsinx$

Bài 22 trang 107 SGK Toán 11 Kết nối

Mùa xuân ở hội Lim (tỉnh Bắc Ninh) thường có trò chơi đu. Khi người chơi đu nhún cây đu sẽ đưa người chơi dao động qua lại quanh vị trí cân bằng. Giả sử khoảng cách h (tính bằng mét) từ người chơi đu đến vị trí cân bằng được tính theo thời gian t (t ≥ 0và được tính bằng giây) bởi hệ thức h = |d| với d = 3cos[ $\frac{\pi }{3}$ (2t − 1)] trong đó ta quy ước rằng d > 0 khi vị trí cân bằng ở về phía sau lưng người chơi đu và d < 0 trong trường hợp ngược lại.

a) Tìm các thời điểm trong vòng 2 giây đầu tiên mà người chơi đu ở xa vị trí cân bằng nhất.

b) Tìm các thời điểm trong vòng 2 giây đầu tiên mà người chơi đu cách vị trí cân bằng 2 m (tính chính xác đến 0,01 giây).

Bài làm

a) Ta có

$cos[\frac{ \pi}{3}(2t-1)] = \pm 1 \Leftrightarrow sin[\frac{ \pi}{3} (2t -1)]=0$

$\Leftrightarrow \frac{\pi}{3}(2t-1) =k \pi \Leftrightarrow t=\frac{1}{2}(3k+1)$

Ta cần tìm k nguyên để 0 ≤ t ≤ 2

$0 \leq t\leq 2 \Leftrightarrow 0 \frac{1}{2} (3k+1)\leq 2$

$\Leftrightarrow -\frac{1}{3}\leq k\leq 1\Leftrightarrow k \in \left \{ 0;1 \right \}$

Với k = 0 thì t = $\frac{1}{2}$ . Với k = 1 thì t = 2. Vậy trong 2 giây đầu tiên, người chơi đu ở xa vị trí cân bằng nhất vào các thời điểm $\frac{1}{2}$ giây và 2 giây.

b)

$3cos [\frac{\pi}{3}(2t-1)]=\pm 2$

$\Leftrightarrow cos^{2}[\frac{\pi}{3}(2t-1)]=\frac{4}{9}$

$\Leftrightarrow 1+cos [\frac{2 \pi}{3}(2t-1)]=\frac{9}{8}$

$\Leftrightarrow cos [\frac{2 \pi}{3}(2t-1)]=-\frac{1}{9}$

$\Leftrightarrow \frac{2\pi }{3}(2t-1)=\pm \alpha +k2 \pi$

$\Leftrightarrow t =\pm \frac{3\alpha }{4 \pi}+\frac{1}{2}+\frac{3k}{2}$

Ta tìm k nguyên để 0 ≤ t ≤ 2

Với $t = \frac{3\alpha }{4 \pi}+\frac{1}{2}+\frac{3k}{2}$

$\Leftrightarrow -\frac{1}{3} -\frac{\alpha}{2 \pi} \leq k \leq 1-\frac{\alpha}{2 \pi}$

Với $cos \alpha = -\frac{1}{9}$

$\Leftrightarrow k =0$ và $t \approx 0,90$

Với $-t = \frac{3\alpha }{4 \pi}+\frac{1}{2}+\frac{3k}{2}$ tương tự

Trong khoảng 2 giây đầu tiên, có ba thời điểm mà người chơi đu cách vị trí cân bằng 2 mét, đó là t $\approx$ 0,10 giây $\approx$ 0,90 giây và t $\approx$ 0,60 giây.

Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Toán 11 Kết nối tri thức bài Ôn tập cuối năm. Mong rằng qua bài viết này bạn đọc có thêm tài liệu để học tập tốt hơn môn Toán 11 Kết nối tri thức. Mời các bạn cùng tham khảo thêm tại mục Ngữ văn 11 Kết nối tri thức.

Đánh giá bài viết

1 93

Bài trước

Bài sau